Question and Answers Forum

AllQuestion and Answers: Page 668

Question Number 151758 Answers: 2 Comments: 1

f(3x+1)=g^(−1) (5x^2 −2) (g o f)^′ (4) = ?

$$\mathrm{f}\left(\mathrm{3x}+\mathrm{1}\right)=\mathrm{g}^{−\mathrm{1}} \left(\mathrm{5x}^{\mathrm{2}} −\mathrm{2}\right) \\ $$$$\left({g}\:{o}\:{f}\right)^{'} \:\left(\mathrm{4}\right)\:=\:? \\ $$

Question Number 151756 Answers: 0 Comments: 1

Question Number 151768 Answers: 1 Comments: 0

∫_0 ^∞ ((ln(1 + a^2 x^2 ))/(b^2 + x^2 )) dx = ?

$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{\mathrm{ln}\left(\mathrm{1}\:+\:\mathrm{a}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} \right)}{\mathrm{b}^{\mathrm{2}} \:+\:\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx}\:=\:? \\ $$

Question Number 151767 Answers: 3 Comments: 0

lim_(n→∞) Σ_(k=1) ^∞ (n/(n^2 + k)) = ?

$$\underset{\boldsymbol{\mathrm{n}}\rightarrow\infty} {\mathrm{lim}}\:\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{n}}{\mathrm{n}^{\mathrm{2}} \:+\:\mathrm{k}}\:=\:? \\ $$

Question Number 151766 Answers: 0 Comments: 1

Question Number 151754 Answers: 0 Comments: 0

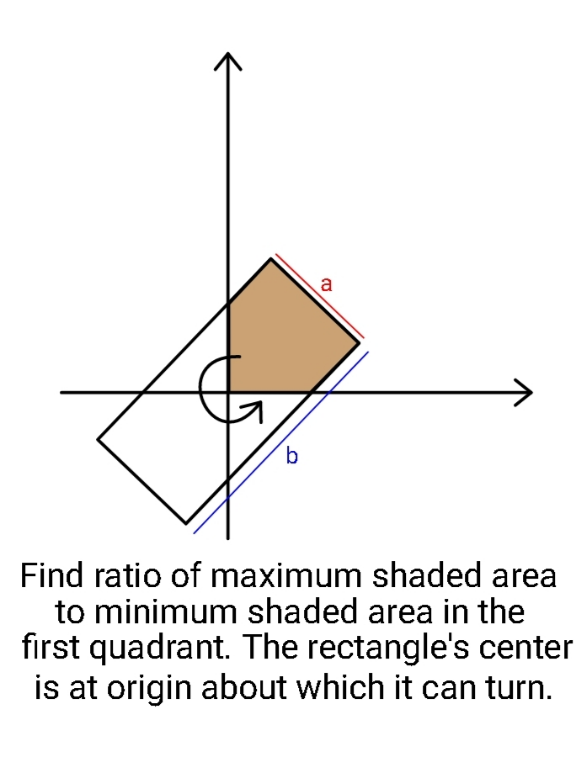
Question Number 151753 Answers: 0 Comments: 1

Question Number 151747 Answers: 1 Comments: 0

let f(x)=((λ-x)/(1+x^2 )) and λ≥((-3)/4) solve in R f(f(f(x))) ≤ 0

$$\mathrm{let}\:\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\lambda-\mathrm{x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\:\mathrm{and}\:\:\lambda\geqslant\frac{-\mathrm{3}}{\mathrm{4}} \\ $$$$\mathrm{solve}\:\mathrm{in}\:\mathbb{R}\:\:\mathrm{f}\left(\mathrm{f}\left(\mathrm{f}\left(\mathrm{x}\right)\right)\right)\:\leqslant\:\mathrm{0} \\ $$

Question Number 151744 Answers: 1 Comments: 0

show that.... F := ∫_0 ^( ∞) (( sin^( 4) (x^( 2) ) )/x^( 2) ) dx = (1/8) ( 4 − (√2) )(√π) .....■ ...m.n...

$$ \\ $$$$\:\:\:\:\:\:\:\:{show}\:\:{that}.... \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathscr{F}\::=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:{sin}^{\:\mathrm{4}} \:\left({x}^{\:\mathrm{2}} \:\right)\:}{{x}^{\:\mathrm{2}} }\:{dx}\:=\:\frac{\mathrm{1}}{\mathrm{8}}\:\left(\:\mathrm{4}\:−\:\sqrt{\mathrm{2}}\:\right)\sqrt{\pi}\:.....\blacksquare\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:...{m}.{n}... \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Question Number 151742 Answers: 1 Comments: 0

F (x ):= ((log (sin(x) +cos (x)))/(log (sin(2x)))) find the Domain of F ... D_( F) =?

$$\:\: \\ $$$$\:\:\:\mathrm{F}\:\left({x}\:\right):=\:\frac{{log}\:\left({sin}\left({x}\right)\:+{cos}\:\left({x}\right)\right)}{{log}\:\left({sin}\left(\mathrm{2}{x}\right)\right)} \\ $$$$\:\:{find}\:\:\:{the}\:{Domain}\:{of}\:\:\:\:\mathrm{F}\:... \\ $$$$\:\:\:\mathrm{D}_{\:\mathrm{F}} \:=? \\ $$

Question Number 151739 Answers: 0 Comments: 0

∫_0 ^( ∞) ((ln(x))/( (√(x^x +1)))) dx

$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{ln}\left({x}\right)}{\:\sqrt{{x}^{{x}} +\mathrm{1}}}\:{dx} \\ $$$$\: \\ $$

Question Number 151738 Answers: 1 Comments: 0

∫_0 ^( 1) x d(e^x^2 ) how it solve

$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \:{x}\:{d}\left({e}^{{x}^{\mathrm{2}} } \right) \\ $$$$ \\ $$$${how}\:{it}\:{solve}\: \\ $$

Question Number 151791 Answers: 1 Comments: 0

Question Number 151790 Answers: 1 Comments: 0

Question Number 151724 Answers: 0 Comments: 10

Question Number 151699 Answers: 2 Comments: 0

Σ_(x^3 +2022x−2021=0) (((1+x)/(1−x))) =?

$$\:\:\:\:\underset{{x}^{\mathrm{3}} +\mathrm{2022}{x}−\mathrm{2021}=\mathrm{0}} {\sum}\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right)\:=? \\ $$

Question Number 151761 Answers: 1 Comments: 0

∫_0 ^( ∞) (1/( (√(e^x +1)))) dx

$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{1}}{\:\sqrt{{e}^{{x}} +\mathrm{1}}}\:{dx}\: \\ $$$$\: \\ $$

Question Number 151685 Answers: 1 Comments: 0

Find maximum value of function α(x)= (√(2x)) +(√(16−x)) +(√(35+x)) .

$$\:\:{Find}\:{maximum}\:{value}\:{of}\:{function} \\ $$$$\:\:\alpha\left({x}\right)=\:\sqrt{\mathrm{2}{x}}\:+\sqrt{\mathrm{16}−{x}}\:+\sqrt{\mathrm{35}+{x}}\:. \\ $$

Question Number 151677 Answers: 1 Comments: 0

Question Number 151673 Answers: 1 Comments: 0

Question Number 151665 Answers: 2 Comments: 0

prove 4arccot5−arccot239=(π/4)

$$\mathrm{prove}\:\mathrm{4arccot5}−\mathrm{arccot239}=\frac{\pi}{\mathrm{4}} \\ $$

Question Number 151721 Answers: 0 Comments: 1

Question Number 151660 Answers: 1 Comments: 0

Question Number 151652 Answers: 1 Comments: 0

faire la division de (1−x^n ) par (1−x)

$${faire}\:{la}\:{division}\:{de}\:\left(\mathrm{1}−{x}^{{n}} \right)\:{par}\:\left(\mathrm{1}−{x}\right) \\ $$

Question Number 151641 Answers: 1 Comments: 0

Question Number 151638 Answers: 1 Comments: 0

∫_( 0) ^( 2𝛑) (1 - cosx)^(10) cos(10x) dx = ?

$$\underset{\:\mathrm{0}} {\overset{\:\mathrm{2}\boldsymbol{\pi}} {\int}}\left(\mathrm{1}\:-\:\mathrm{cos}\boldsymbol{\mathrm{x}}\right)^{\mathrm{10}} \:\mathrm{cos}\left(\mathrm{10x}\right)\:\mathrm{dx}\:=\:? \\ $$

Pg 663 Pg 664 Pg 665 Pg 666 Pg 667 Pg 668 Pg 669 Pg 670 Pg 671 Pg 672

Contact: info@tinkutara.com