
AllQuestion and Answers: Page 666
Question Number 152672 Answers: 1 Comments: 0
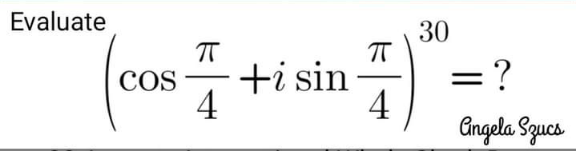
Question Number 152671 Answers: 3 Comments: 2
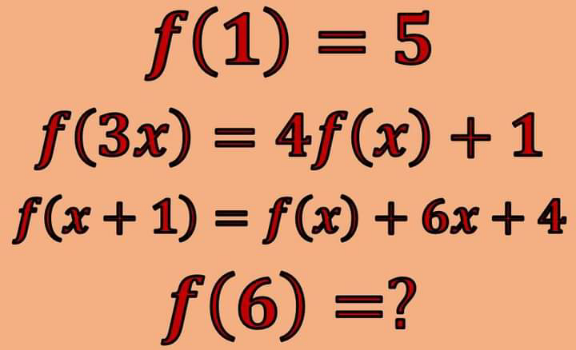
Question Number 152670 Answers: 1 Comments: 0

Question Number 152678 Answers: 2 Comments: 0
Question Number 152663 Answers: 1 Comments: 0
Question Number 152660 Answers: 1 Comments: 0
Question Number 152653 Answers: 1 Comments: 0
Question Number 152652 Answers: 0 Comments: 1

Question Number 152647 Answers: 1 Comments: 1

Question Number 152631 Answers: 1 Comments: 0

Question Number 152626 Answers: 1 Comments: 0
Question Number 152625 Answers: 1 Comments: 2
Question Number 152617 Answers: 0 Comments: 1

Question Number 152608 Answers: 2 Comments: 0
Question Number 152588 Answers: 3 Comments: 0
Question Number 152580 Answers: 1 Comments: 0

Question Number 152576 Answers: 0 Comments: 1
Question Number 152572 Answers: 1 Comments: 0
Question Number 152571 Answers: 1 Comments: 0
Question Number 152620 Answers: 1 Comments: 1

Question Number 152555 Answers: 2 Comments: 0
Question Number 152551 Answers: 1 Comments: 0
Question Number 152546 Answers: 1 Comments: 0
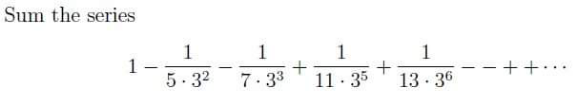
Question Number 152545 Answers: 1 Comments: 0

Question Number 152536 Answers: 1 Comments: 2
Question Number 152533 Answers: 1 Comments: 0

Pg 661 Pg 662 Pg 663 Pg 664 Pg 665 Pg 666 Pg 667 Pg 668 Pg 669 Pg 670
