
AllQuestion and Answers: Page 663
Question Number 153593 Answers: 1 Comments: 0
Question Number 153611 Answers: 3 Comments: 0

Question Number 153596 Answers: 0 Comments: 5

Question Number 153583 Answers: 4 Comments: 3
Question Number 153580 Answers: 1 Comments: 0
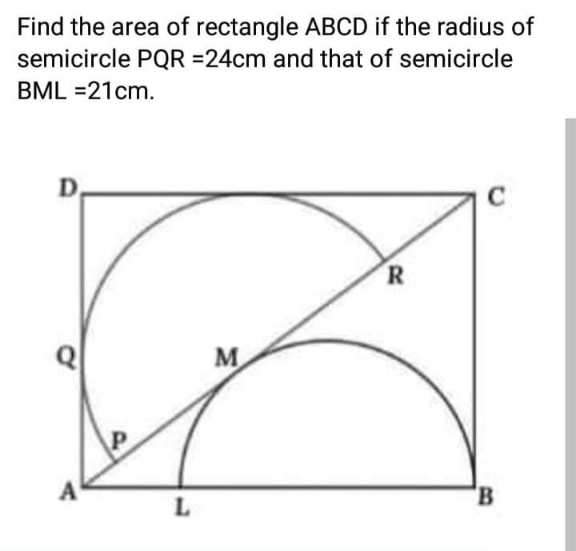
Question Number 153574 Answers: 1 Comments: 0
Question Number 153573 Answers: 1 Comments: 0
Question Number 153572 Answers: 2 Comments: 1
Question Number 153571 Answers: 1 Comments: 0
Question Number 153568 Answers: 1 Comments: 0
Question Number 153565 Answers: 1 Comments: 4
Question Number 153563 Answers: 1 Comments: 0
$$\int\:\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{2}{x}}\:}\:{dx}\:=? \\ $$
Question Number 153555 Answers: 1 Comments: 0
Question Number 153553 Answers: 1 Comments: 0
Question Number 153542 Answers: 1 Comments: 0
Question Number 153537 Answers: 1 Comments: 0

Question Number 153535 Answers: 1 Comments: 0
$${find}\:\int\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{9}}}{{x}^{\mathrm{3}} }\:{dx}=? \\ $$
Question Number 153532 Answers: 0 Comments: 0
Question Number 153518 Answers: 2 Comments: 0
Question Number 153517 Answers: 0 Comments: 2
Question Number 153513 Answers: 2 Comments: 0
Question Number 153512 Answers: 1 Comments: 0
Question Number 153508 Answers: 1 Comments: 0
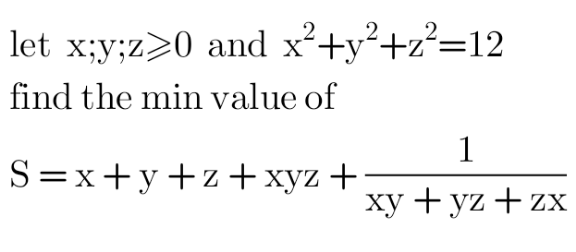
Question Number 153500 Answers: 0 Comments: 0
Question Number 153488 Answers: 0 Comments: 2
Question Number 153486 Answers: 1 Comments: 0
Pg 658 Pg 659 Pg 660 Pg 661 Pg 662 Pg 663 Pg 664 Pg 665 Pg 666 Pg 667
