
AllQuestion and Answers: Page 662
Question Number 153722 Answers: 0 Comments: 0
Question Number 153721 Answers: 2 Comments: 0
Question Number 153716 Answers: 1 Comments: 1

Question Number 153714 Answers: 2 Comments: 0
Question Number 153708 Answers: 2 Comments: 0
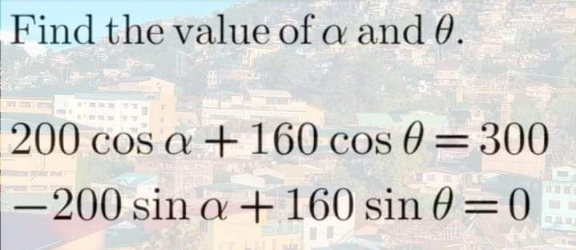
Question Number 153704 Answers: 1 Comments: 1

Question Number 153696 Answers: 1 Comments: 0

Question Number 153867 Answers: 0 Comments: 2
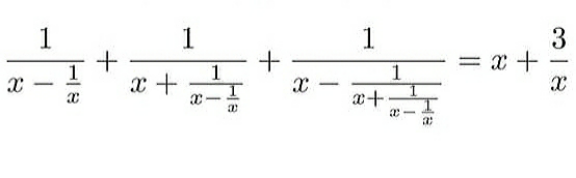
Question Number 153698 Answers: 2 Comments: 0
Question Number 153685 Answers: 3 Comments: 2

Question Number 153682 Answers: 1 Comments: 0
$$\:\left(\sqrt[{{i}}]{{i}}\:\right)^{{xi}} \:=\:{i}^{{x}} \: \\ $$$$\:\:{x}=?\: \\ $$
Question Number 153681 Answers: 1 Comments: 0
Question Number 153679 Answers: 1 Comments: 0
Question Number 153676 Answers: 2 Comments: 0
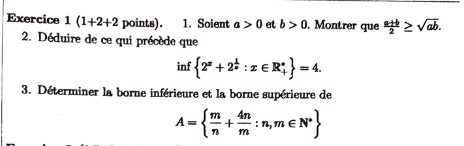
Question Number 153671 Answers: 0 Comments: 1
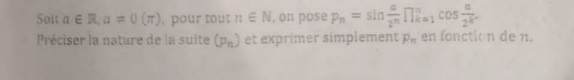
Question Number 153668 Answers: 0 Comments: 0
Question Number 153657 Answers: 0 Comments: 2
Question Number 153651 Answers: 2 Comments: 0
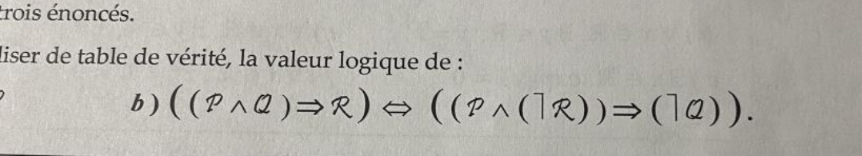
Question Number 153638 Answers: 1 Comments: 2
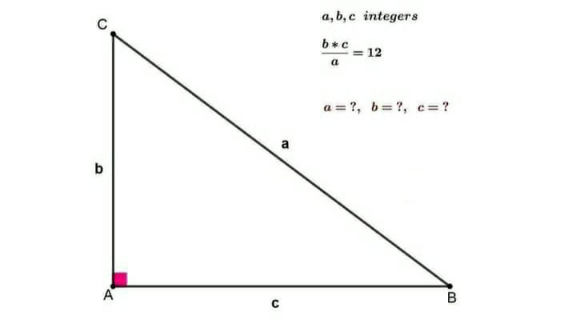
Question Number 153629 Answers: 0 Comments: 3

Question Number 153628 Answers: 1 Comments: 0
Question Number 153626 Answers: 1 Comments: 0
Question Number 153616 Answers: 0 Comments: 1

Question Number 153605 Answers: 1 Comments: 2
Question Number 153598 Answers: 0 Comments: 3
Question Number 153736 Answers: 1 Comments: 0
Pg 657 Pg 658 Pg 659 Pg 660 Pg 661 Pg 662 Pg 663 Pg 664 Pg 665 Pg 666
