
AllQuestion and Answers: Page 661
Question Number 153839 Answers: 1 Comments: 1

Question Number 153829 Answers: 0 Comments: 0
Question Number 153842 Answers: 0 Comments: 0

Question Number 153817 Answers: 0 Comments: 3
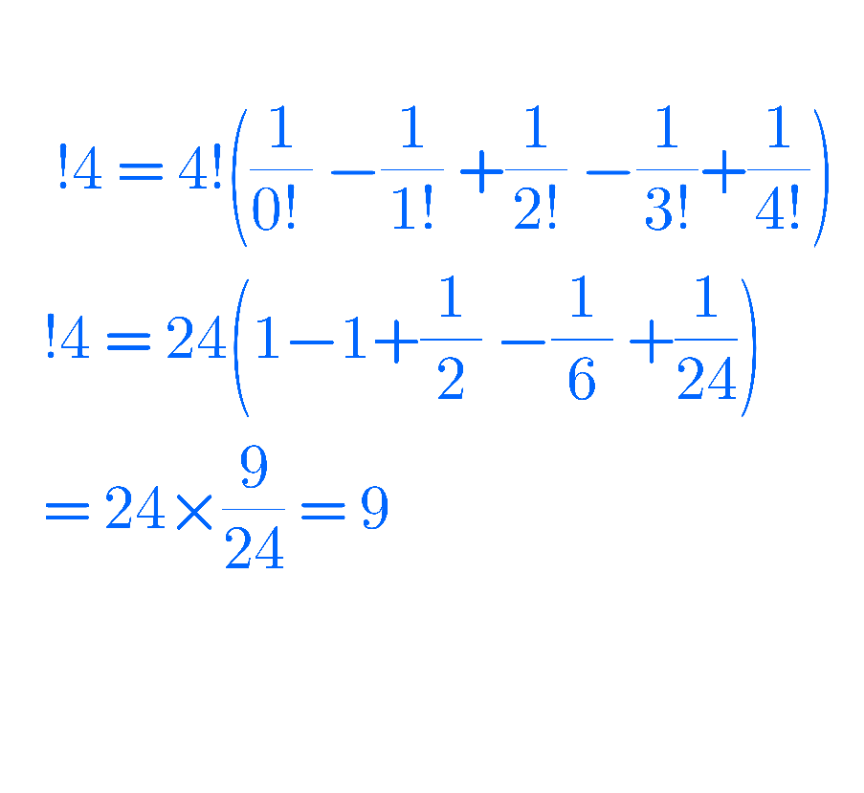
Question Number 153808 Answers: 0 Comments: 0
Question Number 153803 Answers: 1 Comments: 1
Question Number 153800 Answers: 2 Comments: 0

Question Number 153784 Answers: 0 Comments: 1

Question Number 153781 Answers: 1 Comments: 1

Question Number 153780 Answers: 1 Comments: 0
$$\:\lfloor\:\frac{\mathrm{125}}{\mathrm{12}}\:\rfloor\:=\mathrm{10}\:{or}\:\mathrm{11}\:? \\ $$
Question Number 153775 Answers: 1 Comments: 1
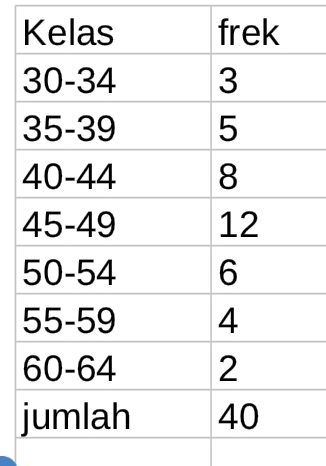
Question Number 153772 Answers: 1 Comments: 2
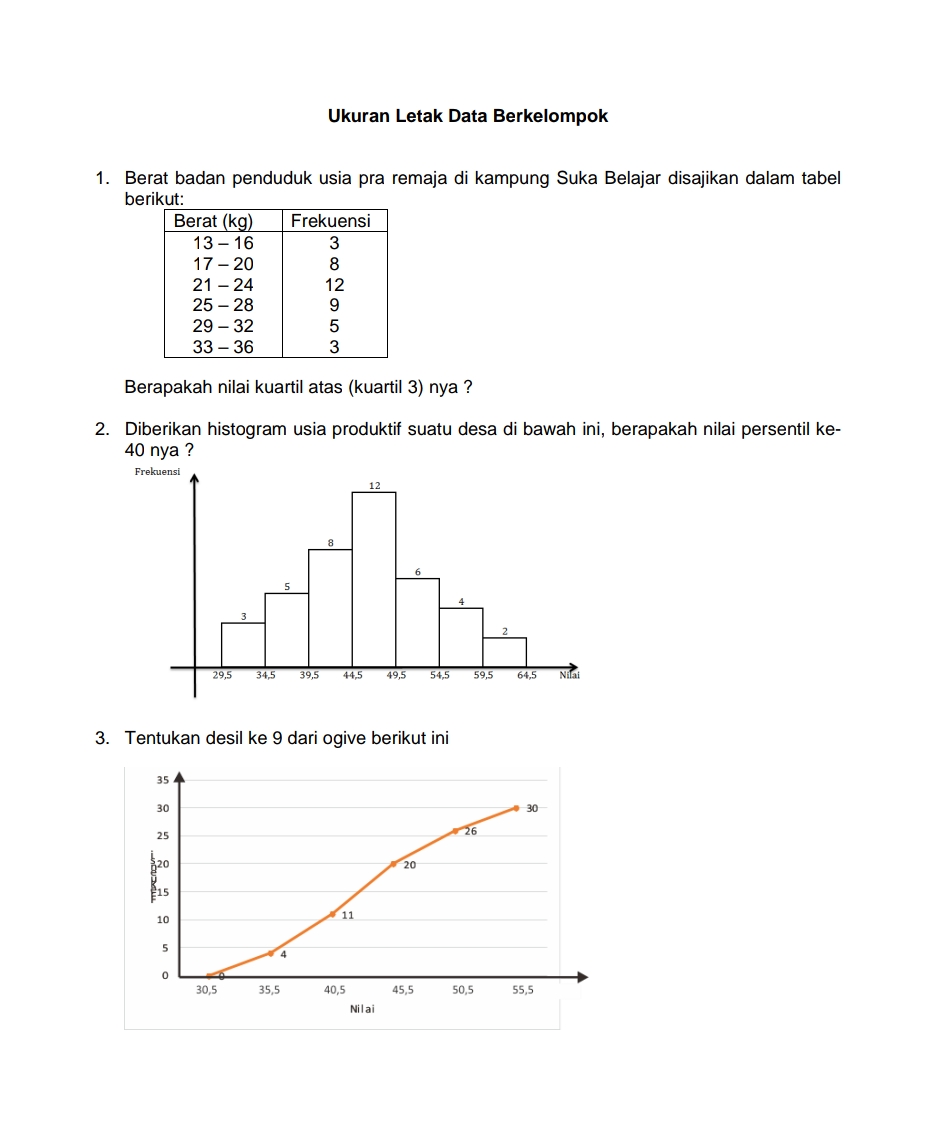
Question Number 153769 Answers: 1 Comments: 0

Question Number 153765 Answers: 2 Comments: 0
Question Number 153764 Answers: 1 Comments: 2
Question Number 153763 Answers: 1 Comments: 0
Question Number 153760 Answers: 1 Comments: 0
$$\int\:\mathrm{sin}^{\mathrm{2}} \mathrm{4}{x}\:\mathrm{cos}\:\mathrm{4}{x}\:{dx}= \\ $$
Question Number 153759 Answers: 0 Comments: 0
Question Number 153757 Answers: 1 Comments: 1
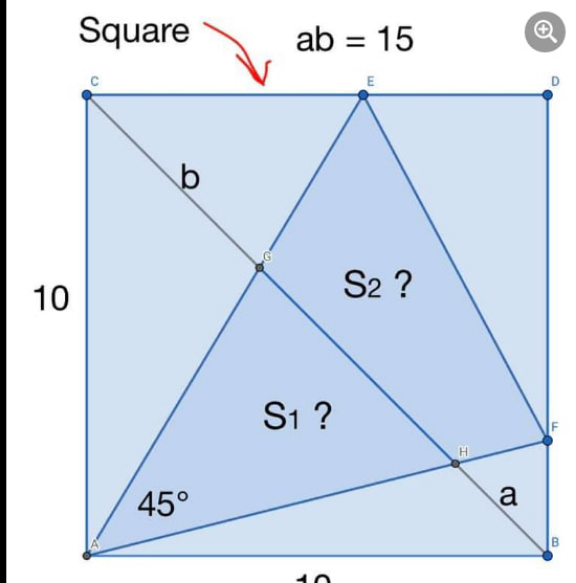
Question Number 153755 Answers: 0 Comments: 0

Question Number 153742 Answers: 1 Comments: 0
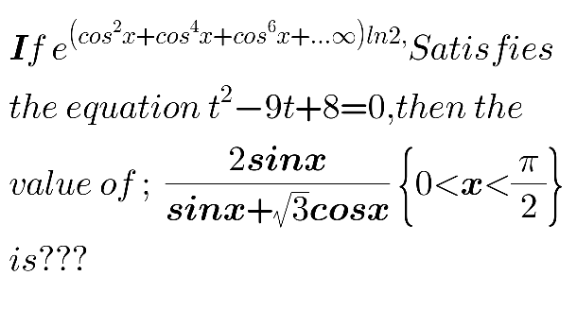
Question Number 153737 Answers: 2 Comments: 0
Question Number 153734 Answers: 0 Comments: 0

Question Number 153733 Answers: 0 Comments: 0

Question Number 153728 Answers: 0 Comments: 0

Question Number 153722 Answers: 0 Comments: 0
Pg 656 Pg 657 Pg 658 Pg 659 Pg 660 Pg 661 Pg 662 Pg 663 Pg 664 Pg 665
