
AllQuestion and Answers: Page 660
Question Number 151468 Answers: 2 Comments: 0
Question Number 151461 Answers: 1 Comments: 0
$$\int\frac{\mathrm{xdx}}{\mathrm{x}^{\mathrm{4}} +\mathrm{4x}^{\mathrm{2}} +\mathrm{5}} \\ $$
Question Number 151460 Answers: 1 Comments: 0
Question Number 151454 Answers: 0 Comments: 2
Question Number 151453 Answers: 0 Comments: 7
Question Number 151449 Answers: 2 Comments: 0
Question Number 151448 Answers: 1 Comments: 2
Question Number 151447 Answers: 1 Comments: 0
Question Number 151444 Answers: 2 Comments: 0
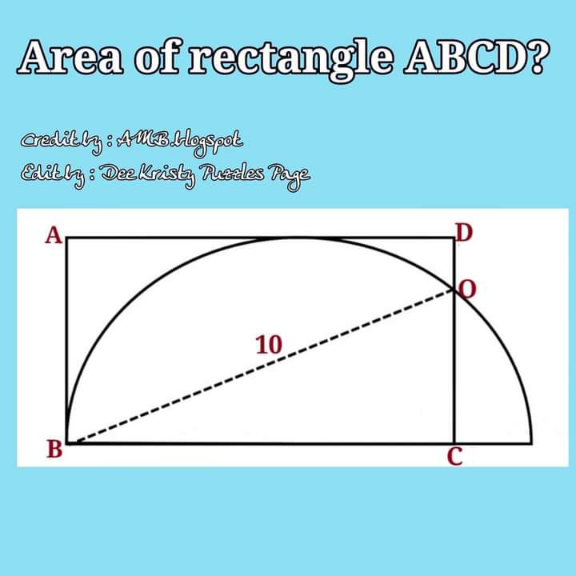
Question Number 151436 Answers: 0 Comments: 0
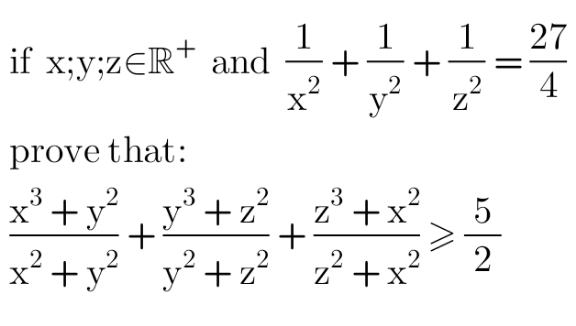
Question Number 151435 Answers: 1 Comments: 4

Question Number 151429 Answers: 1 Comments: 0
Question Number 151428 Answers: 1 Comments: 0
Question Number 151426 Answers: 3 Comments: 0
Question Number 151425 Answers: 2 Comments: 0
Question Number 151423 Answers: 1 Comments: 0
Question Number 151421 Answers: 2 Comments: 2
Question Number 151418 Answers: 1 Comments: 0
Question Number 151415 Answers: 0 Comments: 0
Question Number 151404 Answers: 1 Comments: 1
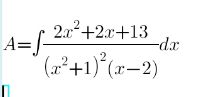
Question Number 151403 Answers: 0 Comments: 5
Question Number 151401 Answers: 1 Comments: 1

Question Number 151393 Answers: 2 Comments: 0
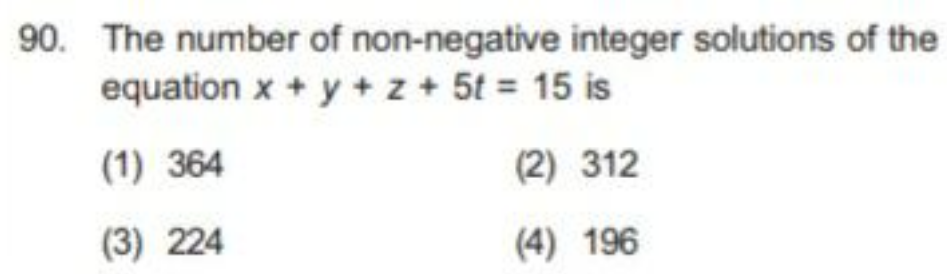
Question Number 151391 Answers: 1 Comments: 0
Question Number 151383 Answers: 1 Comments: 1
Question Number 151377 Answers: 0 Comments: 2
Pg 655 Pg 656 Pg 657 Pg 658 Pg 659 Pg 660 Pg 661 Pg 662 Pg 663 Pg 664
