Question and Answers Forum

AllQuestion and Answers: Page 659

Question Number 153160 Answers: 0 Comments: 0

Find the set: { x ∣ x = ((b∙(a + b))/(a^2 + b^2 )) ; a>0 , b>0}

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{set}: \\ $$$$\left\{\:\mathrm{x}\:\mid\:\mathrm{x}\:=\:\frac{\mathrm{b}\centerdot\left(\mathrm{a}\:+\:\mathrm{b}\right)}{\mathrm{a}^{\mathrm{2}} \:+\:\mathrm{b}^{\mathrm{2}} }\:\:;\:\:\mathrm{a}>\mathrm{0}\:,\:\mathrm{b}>\mathrm{0}\right\} \\ $$

Question Number 153154 Answers: 1 Comments: 0

lim_(x→y) ((sin (e^x )−sin (e^y ))/(x−y))=?

$$\:\:\underset{{x}\rightarrow{y}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left({e}^{{x}} \right)−\mathrm{sin}\:\left({e}^{{y}} \right)}{{x}−{y}}=? \\ $$

Question Number 153153 Answers: 1 Comments: 0

Question Number 153152 Answers: 2 Comments: 0

∫ (√(x^3 +1)) dx

$$\int\:\sqrt{{x}^{\mathrm{3}} +\mathrm{1}}\:{dx} \\ $$

Question Number 153151 Answers: 2 Comments: 0

∫_0 ^1 ((ln(x^3 +1))/(x+1))dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}^{\mathrm{3}} +\mathrm{1}\right)}{{x}+\mathrm{1}}{dx} \\ $$

Question Number 153146 Answers: 1 Comments: 0

Question Number 153128 Answers: 1 Comments: 0

if ((x+y)/2) + (√(xy)) = ((1+(√5))/2) and x^2 +y^2 =(√5) find (1/x) + (1/y) = ?

$$\mathrm{if}\:\:\:\frac{\mathrm{x}+\mathrm{y}}{\mathrm{2}}\:+\:\sqrt{\mathrm{xy}}\:=\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\:\mathrm{and}\:\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\sqrt{\mathrm{5}} \\ $$$$\mathrm{find}\:\:\:\frac{\mathrm{1}}{\mathrm{x}}\:+\:\frac{\mathrm{1}}{\mathrm{y}}\:=\:? \\ $$

Question Number 153127 Answers: 1 Comments: 2

Question Number 153117 Answers: 1 Comments: 0

∫_0 ^1 cot^(−1) (1−x+x^2 )dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{cot}^{−\mathrm{1}} \left(\mathrm{1}−\mathrm{x}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx} \\ $$

Question Number 153114 Answers: 2 Comments: 0

∫_0 ^1 ((log (1+x))/(1+x^2 ))dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{log}\:\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$

Question Number 153112 Answers: 1 Comments: 0

∫_(−π) ^π (sin^(75) x+x^(125) )dx=0

$$\int_{−\pi} ^{\pi} \left(\mathrm{sin}\:^{\mathrm{75}} \mathrm{x}+\mathrm{x}^{\mathrm{125}} \right)\mathrm{dx}=\mathrm{0} \\ $$

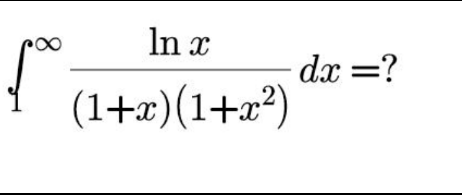
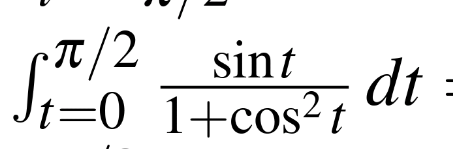
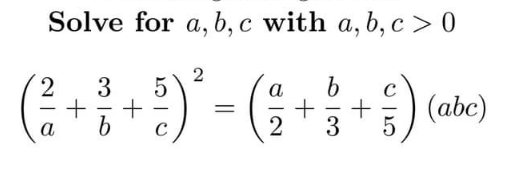
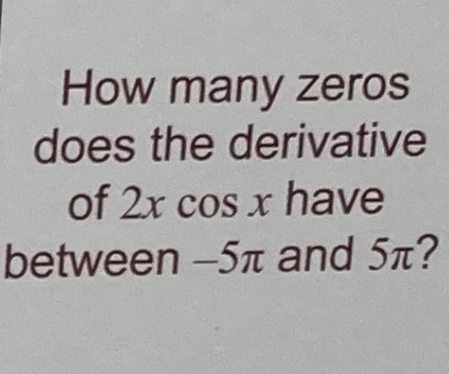
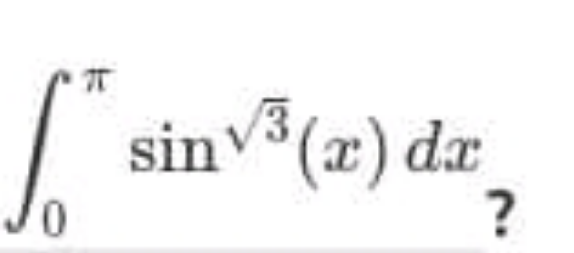
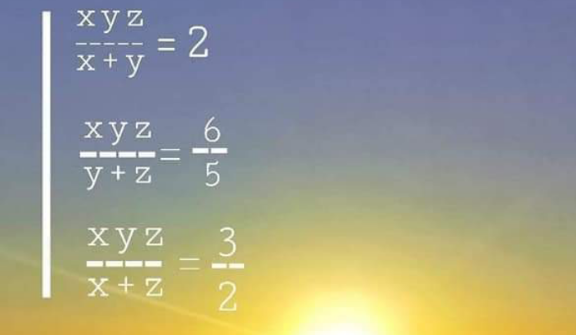
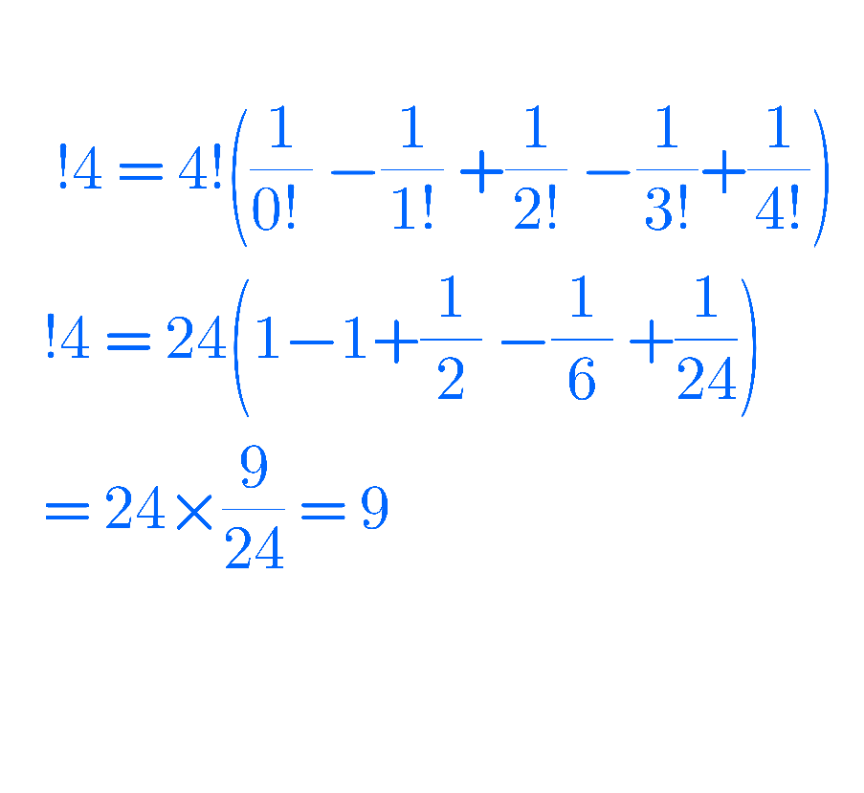
Question Number 153111 Answers: 0 Comments: 0

∫_(−1) ^1 e^x dx as limit of the sum

$$\int_{−\mathrm{1}} ^{\mathrm{1}} \mathrm{e}^{\mathrm{x}} \:\mathrm{dx}\:\mathrm{as}\:\mathrm{limit}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sum} \\ $$

Question Number 153110 Answers: 0 Comments: 0

∫_0 ^1 (3x^2 +2x+1)dx as the limit of sum

$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{3x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}\right)\mathrm{dx}\: \\ $$$$\mathrm{as}\:\mathrm{the}\:\mathrm{limit}\:\:\mathrm{of}\:\mathrm{sum} \\ $$

Question Number 153209 Answers: 0 Comments: 2

Question Number 153104 Answers: 1 Comments: 0

∫_0 ^π (x^3 /(x^3 +(π−x)^3 ))dx=?

$$\int_{\mathrm{0}} ^{\pi} \frac{{x}^{\mathrm{3}} }{{x}^{\mathrm{3}} +\left(\pi−{x}\right)^{\mathrm{3}} }{dx}=? \\ $$

Question Number 153105 Answers: 1 Comments: 0

find ln 𝚪(x) ?

$${find}\:\:\boldsymbol{{ln}}\:\boldsymbol{\Gamma}\left(\boldsymbol{{x}}\right)\:? \\ $$

Question Number 153103 Answers: 1 Comments: 0

(1/(2∙3))+(1/(4∙5∙6))+(1/(7∙8∙9))+…

$$\frac{\mathrm{1}}{\mathrm{2}\centerdot\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}\centerdot\mathrm{5}\centerdot\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{7}\centerdot\mathrm{8}\centerdot\mathrm{9}}+\ldots \\ $$

Question Number 153082 Answers: 1 Comments: 0

Question Number 153079 Answers: 1 Comments: 1

Solve the equation: (√(1-z)) = 2z^2 - 1 + 2z (√(1-z^2 ))

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}: \\ $$$$\sqrt{\mathrm{1}-\boldsymbol{{z}}}\:=\:\mathrm{2}\boldsymbol{{z}}^{\mathrm{2}} \:-\:\mathrm{1}\:+\:\mathrm{2}\boldsymbol{{z}}\:\sqrt{\mathrm{1}-\boldsymbol{{z}}^{\mathrm{2}} } \\ $$

Question Number 153070 Answers: 3 Comments: 0

Find the solution set of inequality (√(3x+4)) ≥ x−2

$$\:\:\:{Find}\:{the}\:{solution}\:{set}\:{of}\:{inequality} \\ $$$$\:\:\:\:\:\:\:\sqrt{\mathrm{3}{x}+\mathrm{4}}\:\geqslant\:{x}−\mathrm{2}\: \\ $$

Question Number 153057 Answers: 1 Comments: 0

Question Number 153056 Answers: 0 Comments: 0

Question Number 153055 Answers: 0 Comments: 0

Question Number 153054 Answers: 1 Comments: 0

Question Number 153053 Answers: 0 Comments: 0

Question Number 153063 Answers: 0 Comments: 5

show that ∫_(−∞) ^( ∞) (1/( (√(x^2 +1)))) dx is unsolvable

$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{show}\:\mathrm{that} \\ $$$$\: \\ $$$$\:\:\:\:\:\int_{−\infty} ^{\:\infty} \:\frac{\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\:\:{dx} \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\mathrm{is}\:\mathrm{unsolvable} \\ $$$$\: \\ $$

Pg 654 Pg 655 Pg 656 Pg 657 Pg 658 Pg 659 Pg 660 Pg 661 Pg 662 Pg 663

Contact: info@tinkutara.com