
AllQuestion and Answers: Page 658
Question Number 154103 Answers: 2 Comments: 2
Question Number 154102 Answers: 0 Comments: 0

Question Number 154100 Answers: 1 Comments: 0
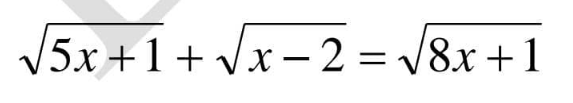
Question Number 154099 Answers: 1 Comments: 0
Question Number 154088 Answers: 1 Comments: 1

Question Number 154087 Answers: 0 Comments: 0
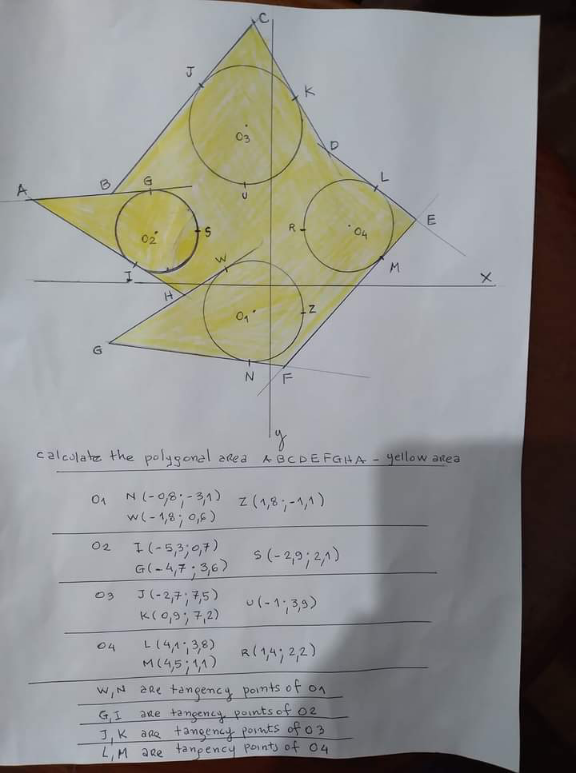
Question Number 154085 Answers: 1 Comments: 1

Question Number 154081 Answers: 1 Comments: 0
Question Number 154080 Answers: 1 Comments: 0
Question Number 154078 Answers: 0 Comments: 1

Question Number 154068 Answers: 3 Comments: 3

Question Number 154065 Answers: 1 Comments: 0

Question Number 154064 Answers: 0 Comments: 0

Question Number 154062 Answers: 0 Comments: 0

Question Number 154059 Answers: 0 Comments: 0
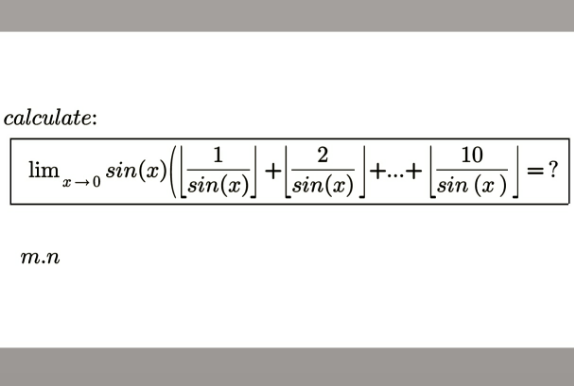
Question Number 154058 Answers: 1 Comments: 0

Question Number 154052 Answers: 0 Comments: 0
Question Number 154051 Answers: 0 Comments: 0
Question Number 154045 Answers: 2 Comments: 1
Question Number 154044 Answers: 0 Comments: 0
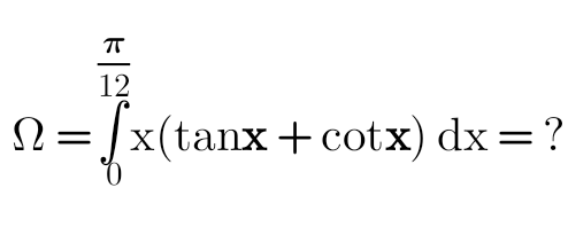
Question Number 154038 Answers: 0 Comments: 1
Question Number 154037 Answers: 0 Comments: 0
Question Number 154036 Answers: 3 Comments: 0
Question Number 154034 Answers: 1 Comments: 0
Question Number 154022 Answers: 0 Comments: 0
Question Number 154020 Answers: 2 Comments: 7
Pg 653 Pg 654 Pg 655 Pg 656 Pg 657 Pg 658 Pg 659 Pg 660 Pg 661 Pg 662
