Question and Answers Forum

AllQuestion and Answers: Page 656

Question Number 152543 Answers: 2 Comments: 0

Solve the equation x^3 −3x=(√(x+2))

$$\:\:\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}\: \\ $$$$\:\mathrm{x}^{\mathrm{3}} −\mathrm{3x}=\sqrt{\mathrm{x}+\mathrm{2}} \\ $$

Question Number 152486 Answers: 1 Comments: 0

Question Number 152544 Answers: 2 Comments: 1

Find the real zeros of the polynomial P_a (x)=(x^2 +1)(x−1)^2 −ax^2 where a is a given real number

$$\:\mathrm{Find}\:\mathrm{the}\:\mathrm{real}\:\mathrm{zeros}\:\mathrm{of}\:\mathrm{the}\:\mathrm{polynomial} \\ $$$$\:\mathrm{P}_{\mathrm{a}} \left(\mathrm{x}\right)=\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{ax}^{\mathrm{2}} \\ $$$$\mathrm{where}\:\mathrm{a}\:\mathrm{is}\:\mathrm{a}\:\mathrm{given}\:\mathrm{real}\:\mathrm{number} \\ $$

Question Number 152481 Answers: 1 Comments: 1

Question Number 152478 Answers: 2 Comments: 0

Question Number 152472 Answers: 1 Comments: 0

Γ((3/4)) = exp(− ((3γ)/4) + ∫_0 ^( 1) f(x)dx) find f(x)

$$\: \\ $$$$\:\:\:\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\:=\:\mathrm{exp}\left(−\:\frac{\mathrm{3}\gamma}{\mathrm{4}}\:+\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {f}\left({x}\right){dx}\right) \\ $$$$\: \\ $$$$\:\:\:\:\mathrm{find}\:{f}\left({x}\right) \\ $$$$\: \\ $$

Question Number 152468 Answers: 1 Comments: 0

∫_(−∞) ^( ∞) ((ln((√(x^4 +1))))/( (√(x^4 +1)))) dx

$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{−\infty} ^{\:\infty} \:\frac{\mathrm{ln}\left(\sqrt{{x}^{\mathrm{4}} +\mathrm{1}}\right)}{\:\sqrt{{x}^{\mathrm{4}} +\mathrm{1}}}\:\:{dx} \\ $$$$\: \\ $$

Question Number 152464 Answers: 1 Comments: 0

Question Number 152457 Answers: 2 Comments: 0

Kofi is 20% heavier than Afia. If Kofi weighs 60 kg what is Afia′s weight?

$$ \\ $$$$\mathrm{Kofi}\:\mathrm{is}\:\mathrm{20\%}\:\:\mathrm{heavier}\:\mathrm{than}\:\mathrm{Afia}.\:\mathrm{If}\:\mathrm{Kofi} \\ $$$$\mathrm{weighs}\:\mathrm{60}\:\mathrm{kg}\:\mathrm{what}\:\mathrm{is}\:\mathrm{Afia}'\mathrm{s}\:\mathrm{weight}? \\ $$

Question Number 152450 Answers: 1 Comments: 1

Question Number 152447 Answers: 1 Comments: 1

Question Number 152445 Answers: 0 Comments: 1

Question Number 152443 Answers: 0 Comments: 2

Question Number 152441 Answers: 3 Comments: 1

Question Number 152439 Answers: 0 Comments: 3

Question Number 152437 Answers: 1 Comments: 1

Question Number 152435 Answers: 1 Comments: 1

Question Number 152433 Answers: 1 Comments: 1

Question Number 152431 Answers: 0 Comments: 3

Question Number 152429 Answers: 1 Comments: 1

Question Number 153758 Answers: 1 Comments: 0

S = ((Σ_(k = 1) ^n sin(θ_k ))/(Σ_(k = 1) ^n cos(θ_k ))); where (θ_k )_(k = 1) ^n is an arithmetic progression. show that S = tan(θ^ ) where θ^ = (1/n)Σ_(k = 1) ^n θ_k is the arithmetic mean of (θ_k )

$${S}\:=\:\frac{\underset{{k}\:=\:\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{sin}\left(\theta_{{k}} \right)}{\underset{{k}\:=\:\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{cos}\left(\theta_{{k}} \right)};\:\mathrm{where}\:\left(\theta_{{k}} \right)_{{k}\:=\:\mathrm{1}} ^{{n}} \:\mathrm{is}\:\mathrm{an}\:\mathrm{arithmetic}\:\mathrm{progression}. \\ $$$$\mathrm{show}\:\mathrm{that}\:{S}\:=\:\mathrm{tan}\left(\bar {\theta}\right) \\ $$$$\mathrm{where}\:\bar {\theta}\:=\:\frac{\mathrm{1}}{{n}}\underset{{k}\:=\:\mathrm{1}} {\overset{{n}} {\sum}}\theta_{{k}} \:\mathrm{is}\:\mathrm{the}\:\mathrm{arithmetic}\:\mathrm{mean}\:\mathrm{of}\:\left(\theta_{{k}} \right) \\ $$

Question Number 152420 Answers: 2 Comments: 0

∫_0 ^( (π/2)) (e^(sinx) /(e^(cosx) +e^(sinx) ))dx ?

$$\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\frac{{e}^{{sinx}} }{{e}^{{cosx}} +{e}^{{sinx}} }{dx}\:\:\:? \\ $$

Question Number 152418 Answers: 1 Comments: 0

Anecdote historique (une vraie anecdote confirme^ e par les historiens). Au XVIIIe^ me sie^ cle, Voltaire est parti aupre^ s de Fre^ de^ ric II de Prusse. Ces deux hommes ont longtemps correspondu avant de se rencontrer. Fre^ de^ ric II e^ tait un ve^ ritable lettre^ qui aimait la philosophie, l′art et les sciences. Voltaire l′admirait beaucoup et le prenait pour un roi philosophe. Fre^ de^ ric II adressait re^ gulie^ rement des petits mots code^ s a^ Voltaire. Un jour il envoie : (p/(venez)) a ((ci)/(100)) Ce a^ quoi Voltaire re^ pond : Ga Comprenez−vous leur correspondance ? Je repre^ cise qu′il s′agit bien d′une correspondance re^ elle entre ces deux personnnages historiques.

$$\boldsymbol{\mathrm{Anecdote}}\:\boldsymbol{\mathrm{historique}} \\ $$$$ \\ $$$$\left({une}\:{vraie}\:{anecdote}\:{confirm}\acute {{e}e}\:{par}\right. \\ $$$$\left.{les}\:{historiens}\right). \\ $$$$ \\ $$$$\mathrm{Au}\:\mathrm{XVIII}\grave {{e}me}\:\mathrm{si}\grave {\mathrm{e}cle},\:\mathrm{Voltaire}\:\mathrm{est}\:\mathrm{parti} \\ $$$$\mathrm{aupr}\grave {\mathrm{e}s}\:\mathrm{de}\:\mathrm{Fr}\acute {\mathrm{e}d}\acute {\mathrm{e}ric}\:\mathrm{II}\:\mathrm{de}\:\mathrm{Prusse}.\:\mathrm{Ces} \\ $$$$\mathrm{deux}\:\mathrm{hommes}\:\mathrm{ont}\:\mathrm{longtemps} \\ $$$$\mathrm{correspondu}\:\mathrm{avant}\:\mathrm{de}\:\mathrm{se}\:\mathrm{rencontrer}. \\ $$$$ \\ $$$$\mathrm{Fr}\acute {\mathrm{e}d}\acute {\mathrm{e}ric}\:\mathrm{II}\:\acute {\mathrm{e}tait}\:\mathrm{un}\:\mathrm{v}\acute {\mathrm{e}ritable}\:\mathrm{lettr}\acute {\mathrm{e}}\:\mathrm{qui} \\ $$$$\mathrm{aimait}\:\mathrm{la}\:\mathrm{philosophie},\:\mathrm{l}'\mathrm{art}\:\mathrm{et}\:\mathrm{les} \\ $$$$\mathrm{sciences}.\:\mathrm{Voltaire}\:\mathrm{l}'\mathrm{admirait}\:\mathrm{beaucoup} \\ $$$$\mathrm{et}\:\mathrm{le}\:\mathrm{prenait}\:\mathrm{pour}\:\mathrm{un}\:\mathrm{roi}\:\mathrm{philosophe}. \\ $$$$ \\ $$$$\mathrm{Fr}\acute {\mathrm{e}d}\acute {\mathrm{e}ric}\:\mathrm{II}\:\mathrm{adressait}\:\mathrm{r}\acute {\mathrm{e}guli}\grave {\mathrm{e}rement} \\ $$$$\mathrm{des}\:\mathrm{petits}\:\mathrm{mots}\:\mathrm{cod}\acute {\mathrm{e}s}\:\grave {\mathrm{a}}\:\mathrm{Voltaire}. \\ $$$$ \\ $$$$\mathrm{Un}\:\mathrm{jour}\:\mathrm{il}\:\mathrm{envoie}\:: \\ $$$$ \\ $$$$\frac{\mathrm{p}}{\mathrm{venez}}\:\mathrm{a}\:\frac{\mathrm{ci}}{\mathrm{100}} \\ $$$$ \\ $$$$\mathrm{Ce}\:\grave {\mathrm{a}}\:\mathrm{quoi}\:\mathrm{Voltaire}\:\mathrm{r}\acute {\mathrm{e}pond}\:: \\ $$$$ \\ $$$$\mathrm{Ga} \\ $$$$ \\ $$$$\mathrm{Comprenez}−\mathrm{vous}\:\mathrm{leur} \\ $$$$\mathrm{correspondance}\:? \\ $$$$ \\ $$$${J}\mathrm{e}\:{repr}\acute {{e}cise}\:{qu}'{il}\:{s}'{agit}\:{bien}\:{d}'{une} \\ $$$${correspondance}\:{r}\acute {{e}elle}\:{entre}\:{ces}\:{deux} \\ $$$${personnnages}\:{historiques}. \\ $$

Question Number 152417 Answers: 0 Comments: 1

Blague de matheux. Les mathe^ maticiens n′urinent pas. Ils font ππ. Bon ok je sors...

$$\boldsymbol{\mathrm{Blague}}\:\boldsymbol{\mathrm{de}}\:\boldsymbol{\mathrm{matheux}}. \\ $$$$ \\ $$$$\mathrm{Les}\:\mathrm{math}\acute {\mathrm{e}maticiens}\:\mathrm{n}'\mathrm{urinent}\:\mathrm{pas}. \\ $$$$ \\ $$$$\mathrm{Ils}\:\mathrm{font}\:\pi\pi. \\ $$$$ \\ $$$$\mathrm{Bon}\:\mathrm{ok}\:\mathrm{je}\:\mathrm{sors}... \\ $$

Question Number 152407 Answers: 2 Comments: 0

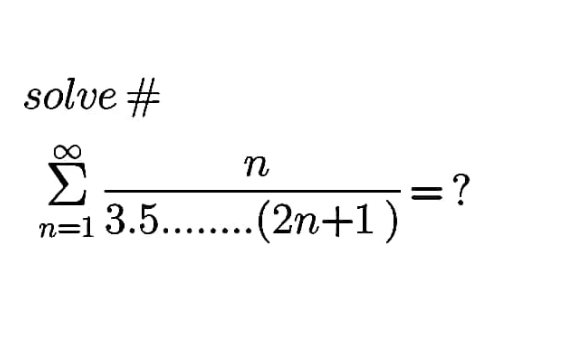
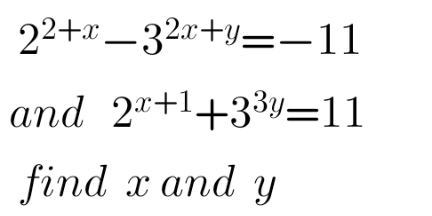
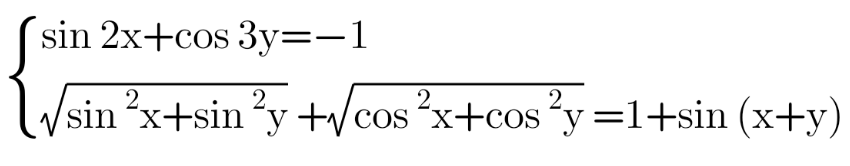
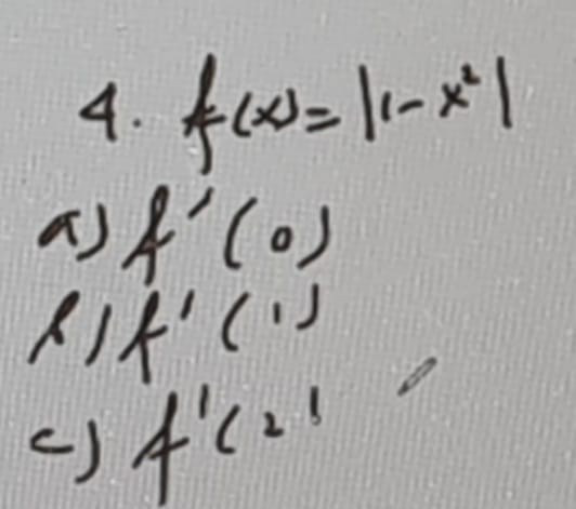
Question Number 152396 Answers: 1 Comments: 0

If x^3 -x+3=0 has the roots a;b and c determine the monic polynomial with the roots a^5 ; b^5 and c^5 .

$$\mathrm{If}\:\:\mathrm{x}^{\mathrm{3}} -\mathrm{x}+\mathrm{3}=\mathrm{0}\:\:\mathrm{has}\:\mathrm{the}\:\mathrm{roots}\:\:\mathrm{a};\mathrm{b}\:\:\mathrm{and}\:\:\mathrm{c} \\ $$$$\mathrm{determine}\:\mathrm{the}\:\mathrm{monic}\:\mathrm{polynomial}\:\mathrm{with} \\ $$$$\mathrm{the}\:\mathrm{roots}\:\:\mathrm{a}^{\mathrm{5}} \:;\:\mathrm{b}^{\mathrm{5}} \:\:\mathrm{and}\:\:\mathrm{c}^{\mathrm{5}} \:. \\ $$

Pg 651 Pg 652 Pg 653 Pg 654 Pg 655 Pg 656 Pg 657 Pg 658 Pg 659 Pg 660

Contact: info@tinkutara.com