
AllQuestion and Answers: Page 655
Question Number 154409 Answers: 1 Comments: 0
Question Number 154407 Answers: 0 Comments: 2
$${How}\:{to}\:{do}\:{it}\:{by}\:\subset\:{and}\:\supset\:? \\ $$
Question Number 154402 Answers: 0 Comments: 2
Question Number 154401 Answers: 3 Comments: 0
Question Number 154400 Answers: 1 Comments: 0
Question Number 154398 Answers: 1 Comments: 0

Question Number 154395 Answers: 1 Comments: 1
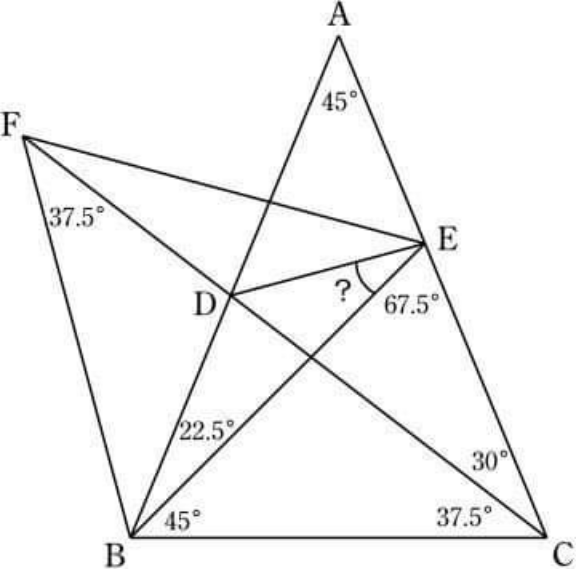
Question Number 154396 Answers: 1 Comments: 0

Question Number 154390 Answers: 1 Comments: 1
Question Number 154385 Answers: 2 Comments: 0
Question Number 154383 Answers: 0 Comments: 0
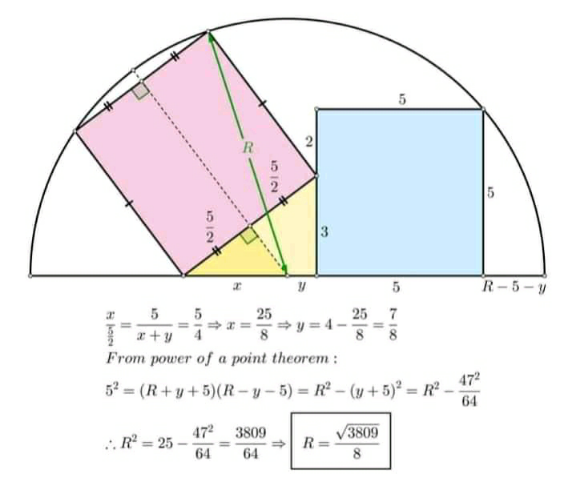
Question Number 154384 Answers: 1 Comments: 0
Question Number 154380 Answers: 1 Comments: 0
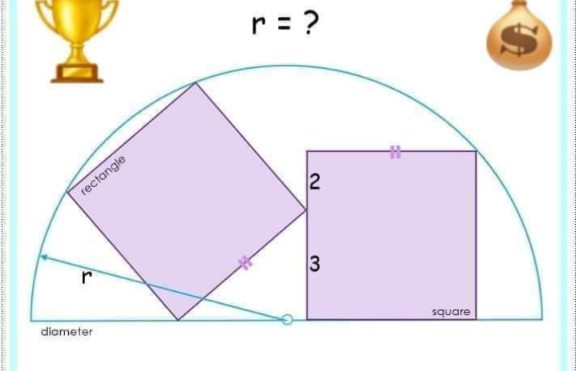
Question Number 154372 Answers: 0 Comments: 0
Question Number 154368 Answers: 0 Comments: 0

Question Number 154365 Answers: 0 Comments: 0

Question Number 154359 Answers: 1 Comments: 0
Question Number 154353 Answers: 1 Comments: 4
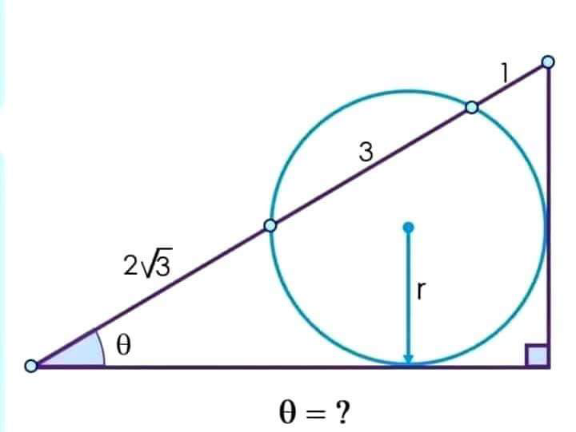
Question Number 154352 Answers: 0 Comments: 0
Question Number 154351 Answers: 3 Comments: 0
Question Number 154343 Answers: 1 Comments: 0
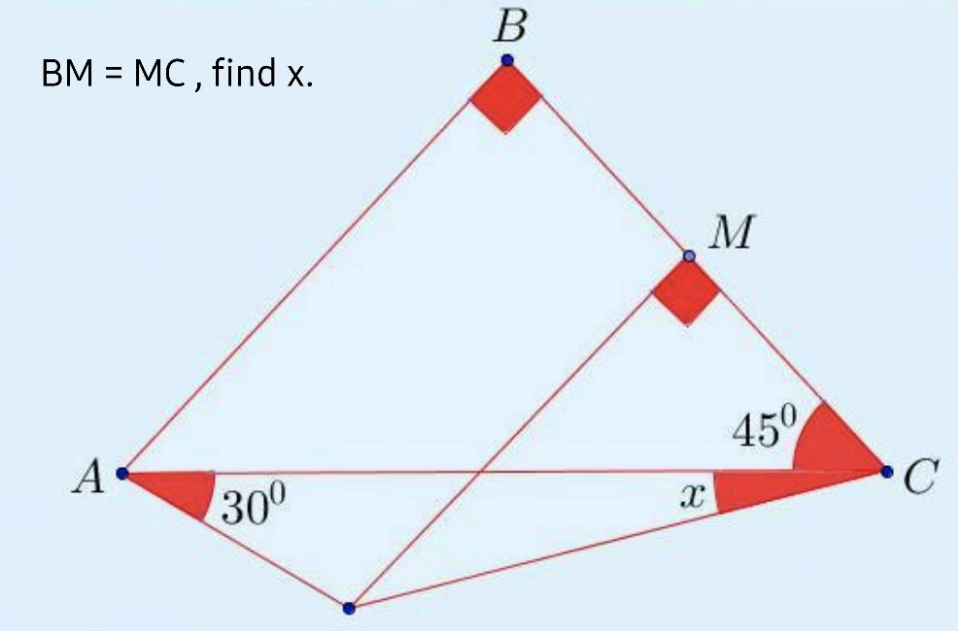
Question Number 154337 Answers: 2 Comments: 0
Question Number 154334 Answers: 3 Comments: 1
Question Number 154328 Answers: 2 Comments: 0
Question Number 154330 Answers: 1 Comments: 0

Question Number 154321 Answers: 2 Comments: 0

Pg 650 Pg 651 Pg 652 Pg 653 Pg 654 Pg 655 Pg 656 Pg 657 Pg 658 Pg 659
