
AllQuestion and Answers: Page 653
Question Number 154651 Answers: 1 Comments: 0
Question Number 154648 Answers: 0 Comments: 0

Question Number 154647 Answers: 1 Comments: 0
Question Number 154641 Answers: 2 Comments: 0
$$\int\frac{\mathrm{1}−\sqrt{{x}}}{\:\sqrt{\mathrm{1}−{x}}}{dx} \\ $$
Question Number 154640 Answers: 2 Comments: 0
$$\underset{\mathrm{1}} {\overset{\mathrm{89}} {\sum}}{sin}^{\mathrm{2}} \left({x}\right)=? \\ $$
Question Number 154622 Answers: 0 Comments: 0

Question Number 154613 Answers: 0 Comments: 3
Question Number 154621 Answers: 2 Comments: 1
$$\:\int\:\frac{\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{{x}^{\mathrm{2}} +{x}}\:{dx}\: \\ $$
Question Number 154599 Answers: 1 Comments: 1

Question Number 154596 Answers: 0 Comments: 0
Question Number 154593 Answers: 1 Comments: 1

Question Number 154594 Answers: 0 Comments: 2

Question Number 154561 Answers: 1 Comments: 0

Question Number 154557 Answers: 0 Comments: 0
Question Number 154554 Answers: 2 Comments: 1

Question Number 154553 Answers: 0 Comments: 0
Question Number 154552 Answers: 2 Comments: 28

Question Number 154549 Answers: 4 Comments: 1
Question Number 154547 Answers: 1 Comments: 0
Question Number 154573 Answers: 2 Comments: 1

Question Number 154544 Answers: 0 Comments: 0
Question Number 154542 Answers: 1 Comments: 0

Question Number 154530 Answers: 0 Comments: 0

Question Number 154516 Answers: 0 Comments: 0
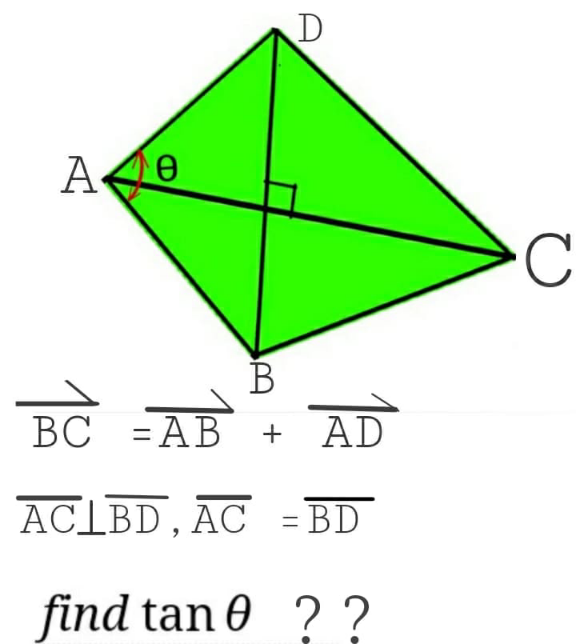
Question Number 154514 Answers: 0 Comments: 1

Question Number 154586 Answers: 1 Comments: 0

Pg 648 Pg 649 Pg 650 Pg 651 Pg 652 Pg 653 Pg 654 Pg 655 Pg 656 Pg 657
