Question and Answers Forum

AllQuestion and Answers: Page 652

Question Number 154148 Answers: 1 Comments: 0

z^4 - ((50)/(2z^4 - 7)) = 14 ⇒ z = ?

$$\boldsymbol{{z}}^{\mathrm{4}} \:-\:\frac{\mathrm{50}}{\mathrm{2}\boldsymbol{{z}}^{\mathrm{4}} \:-\:\mathrm{7}}\:=\:\mathrm{14}\:\:\:\Rightarrow\:\:\:\boldsymbol{{z}}\:=\:? \\ $$

Question Number 154143 Answers: 2 Comments: 0

Question Number 154142 Answers: 2 Comments: 0

Question Number 154138 Answers: 1 Comments: 0

Question Number 154133 Answers: 2 Comments: 0

Given f(x)=((x+(√(1+x^2 ))))^(1/3) +((x−(√(1+x^2 ))))^(1/3) Find f^(−1) (x)=?

$$\mathrm{Given}\:\mathrm{f}\left(\mathrm{x}\right)=\sqrt[{\mathrm{3}}]{\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}+\sqrt[{\mathrm{3}}]{\mathrm{x}−\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }} \\ $$$$\mathrm{Find}\:\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}\right)=? \\ $$

Question Number 154131 Answers: 0 Comments: 1

A long distance runner runs 14km 30°north of east, 7km 60° north of west, 6km 30° south of west, and finally 4km south. Find his final distance and direction relative to the starting point?

$$ \\ $$A long distance runner runs 14km 30°north of east, 7km 60° north of west, 6km 30° south of west, and finally 4km south. Find his final distance and direction relative to the starting point?

Question Number 154200 Answers: 1 Comments: 0

g(((x−1)/(x+1)))=((7x+3)/(x+1)) and f(x^2 −2x+3)=3x^2 −6x+7 find (f+g)(x)=?

$${g}\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)=\frac{\mathrm{7}{x}+\mathrm{3}}{{x}+\mathrm{1}}\:\:{and}\:\:{f}\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{3}\right)=\mathrm{3}{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{7} \\ $$$${find}\:\:\left({f}+{g}\right)\left({x}\right)=?\:\:\: \\ $$

Question Number 154116 Answers: 0 Comments: 0

Question Number 154104 Answers: 3 Comments: 0

∫ e^(√x) dx =?

$$\:\:\int\:{e}^{\sqrt{{x}}} \:{dx}\:=? \\ $$

Question Number 154103 Answers: 2 Comments: 2

si w est une racine cubique de 1 different de 1,alors: (1+w−w^2 )^7 =?

$${si}\:{w}\:{est}\:{une}\:{racine}\:{cubique}\:{de}\:\mathrm{1}\:{different}\:{de}\:\mathrm{1},{alors}: \\ $$$$\left(\mathrm{1}+{w}−{w}^{\mathrm{2}} \right)^{\mathrm{7}} =? \\ $$

Question Number 154102 Answers: 0 Comments: 0

Question Number 154100 Answers: 1 Comments: 0

Question Number 154099 Answers: 1 Comments: 0

{ ((x^2 +y(√(xy)) = 72)),((y^2 +x(√(xy)) = 36)) :}

$$\:\begin{cases}{{x}^{\mathrm{2}} +{y}\sqrt{{xy}}\:=\:\mathrm{72}}\\{{y}^{\mathrm{2}} +{x}\sqrt{{xy}}\:=\:\mathrm{36}}\end{cases} \\ $$

Question Number 154088 Answers: 1 Comments: 1

Question Number 154087 Answers: 0 Comments: 0

Question Number 154085 Answers: 1 Comments: 1

Question Number 154081 Answers: 1 Comments: 0

lim_(x→∞) ((32x^5 −14x^4 +3))^(1/5) −((128x^7 +6x^6 −1))^(1/7) =?

$$\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\sqrt[{\mathrm{5}}]{\mathrm{32}{x}^{\mathrm{5}} −\mathrm{14}{x}^{\mathrm{4}} +\mathrm{3}}−\sqrt[{\mathrm{7}}]{\mathrm{128}{x}^{\mathrm{7}} +\mathrm{6}{x}^{\mathrm{6}} −\mathrm{1}}\:=? \\ $$

Question Number 154080 Answers: 1 Comments: 0

Ω =∫_0 ^( (π/2)) ln^2 (((1+sin t)/(1−sin t)))dt

$$\:\:\:\:\Omega\:=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\:^{\mathrm{2}} \left(\frac{\mathrm{1}+\mathrm{sin}\:{t}}{\mathrm{1}−\mathrm{sin}\:{t}}\right){dt} \\ $$

Question Number 154078 Answers: 0 Comments: 1

Question Number 154068 Answers: 3 Comments: 3

Question Number 154065 Answers: 1 Comments: 0

Question Number 154064 Answers: 0 Comments: 0

Question Number 154062 Answers: 0 Comments: 0

Question Number 154059 Answers: 0 Comments: 0

Question Number 154058 Answers: 1 Comments: 0

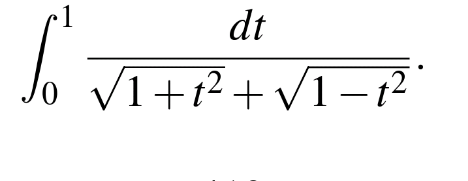
Question Number 154052 Answers: 0 Comments: 0

Prove without any software ∫_( 2−(√3)) ^( 1) e^(−x^2 ) dx < (𝛑/6) and∫_( 1) ^( 2+(√3)) e^(−x^2 ) dx < (𝛑/6)

$$\mathrm{Prove}\:\mathrm{without}\:\mathrm{any}\:\mathrm{software} \\ $$$$\underset{\:\mathrm{2}−\sqrt{\mathrm{3}}} {\overset{\:\mathrm{1}} {\int}}\:\mathrm{e}^{−\boldsymbol{\mathrm{x}}^{\mathrm{2}} } \:\mathrm{dx}\:<\:\frac{\boldsymbol{\pi}}{\mathrm{6}}\:\:\mathrm{and}\underset{\:\mathrm{1}} {\overset{\:\mathrm{2}+\sqrt{\mathrm{3}}} {\int}}\mathrm{e}^{−\boldsymbol{\mathrm{x}}^{\mathrm{2}} } \:\mathrm{dx}\:<\:\frac{\boldsymbol{\pi}}{\mathrm{6}} \\ $$

Pg 647 Pg 648 Pg 649 Pg 650 Pg 651 Pg 652 Pg 653 Pg 654 Pg 655 Pg 656

Contact: info@tinkutara.com