
AllQuestion and Answers: Page 651
Question Number 154892 Answers: 1 Comments: 2
Question Number 154889 Answers: 0 Comments: 0

Question Number 154888 Answers: 1 Comments: 0

Question Number 154926 Answers: 1 Comments: 0
Question Number 154927 Answers: 1 Comments: 0
Question Number 154880 Answers: 6 Comments: 0
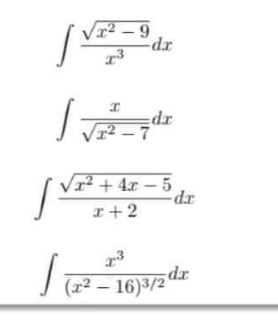
Question Number 154877 Answers: 2 Comments: 1
Question Number 154876 Answers: 1 Comments: 0
Question Number 154875 Answers: 1 Comments: 0

Question Number 154872 Answers: 1 Comments: 0
Question Number 154910 Answers: 1 Comments: 2

Question Number 154860 Answers: 0 Comments: 0
Question Number 154857 Answers: 1 Comments: 0
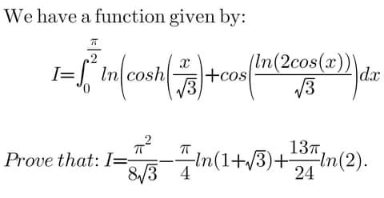
Question Number 154854 Answers: 1 Comments: 1

Question Number 154853 Answers: 1 Comments: 0

Question Number 154851 Answers: 0 Comments: 7

Question Number 154849 Answers: 1 Comments: 0
Question Number 154846 Answers: 0 Comments: 2
Question Number 154823 Answers: 1 Comments: 0
Question Number 154824 Answers: 1 Comments: 0
Question Number 154805 Answers: 0 Comments: 2
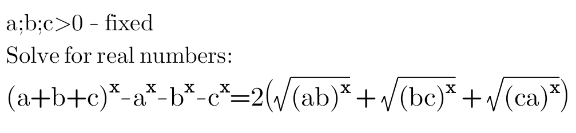
Question Number 154804 Answers: 2 Comments: 1
Question Number 154794 Answers: 0 Comments: 1

Question Number 154786 Answers: 0 Comments: 0
Question Number 154785 Answers: 0 Comments: 3
Question Number 154780 Answers: 3 Comments: 0
Pg 646 Pg 647 Pg 648 Pg 649 Pg 650 Pg 651 Pg 652 Pg 653 Pg 654 Pg 655
