
AllQuestion and Answers: Page 650
Question Number 155013 Answers: 2 Comments: 0
Question Number 155017 Answers: 1 Comments: 0
Question Number 154994 Answers: 1 Comments: 0
Question Number 154993 Answers: 0 Comments: 0
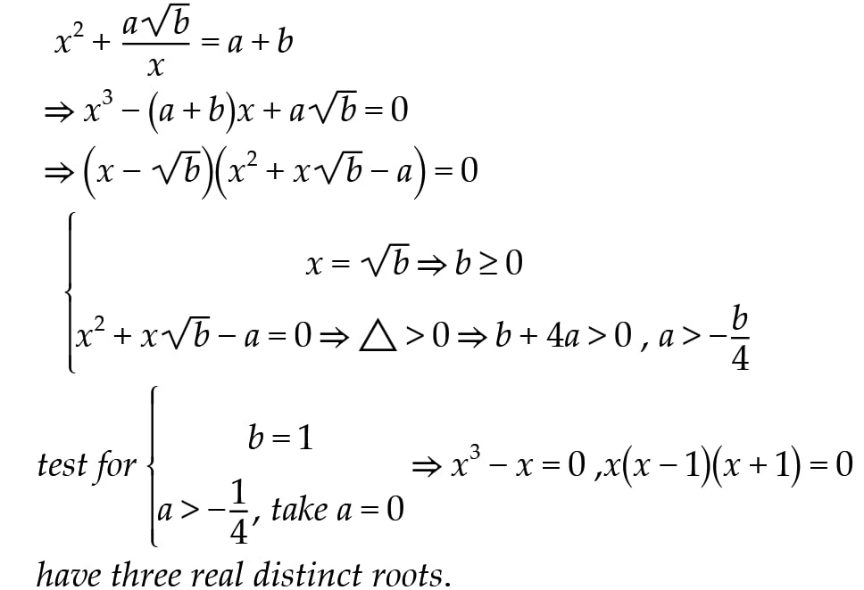
Question Number 154992 Answers: 1 Comments: 0
Question Number 154989 Answers: 2 Comments: 0
Question Number 154987 Answers: 1 Comments: 1
$$\int_{\mathrm{0}} ^{\:\infty} \:\frac{{x}^{{c}} }{{c}^{{x}} }\:\:{dx} \\ $$
Question Number 154986 Answers: 2 Comments: 0
Question Number 154980 Answers: 1 Comments: 0
Question Number 154976 Answers: 0 Comments: 0

Question Number 154975 Answers: 0 Comments: 0
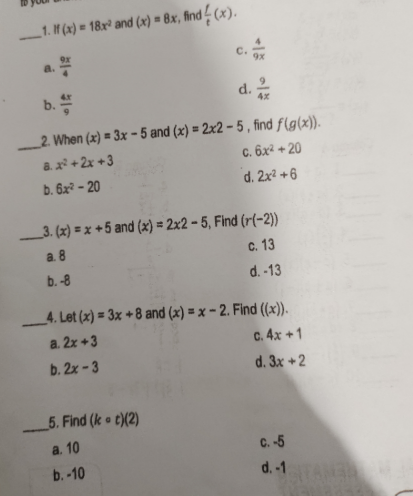
Question Number 154973 Answers: 1 Comments: 0
Question Number 154972 Answers: 0 Comments: 2
Question Number 154966 Answers: 0 Comments: 1
Question Number 154959 Answers: 2 Comments: 2
Question Number 154958 Answers: 0 Comments: 3
Question Number 154948 Answers: 0 Comments: 3
Question Number 154942 Answers: 2 Comments: 0

Question Number 154940 Answers: 1 Comments: 0

Question Number 154931 Answers: 2 Comments: 0
Question Number 154930 Answers: 0 Comments: 1
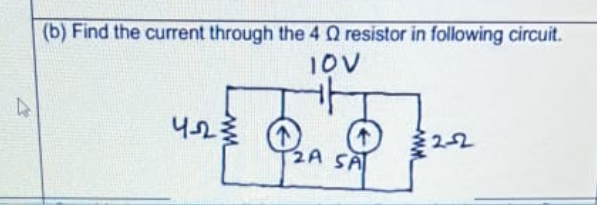
Question Number 154928 Answers: 0 Comments: 0
Question Number 154907 Answers: 0 Comments: 2
Question Number 154902 Answers: 0 Comments: 1
$$\int_{\mathrm{0}} ^{\frac{\mathrm{3}}{\mathrm{2}}} {E}\left({x}^{\mathrm{2}} \right){dx} \\ $$
Question Number 154896 Answers: 0 Comments: 2
Question Number 154893 Answers: 0 Comments: 0
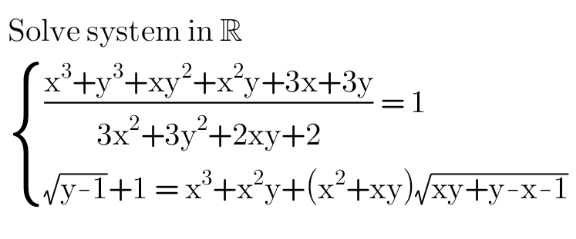
Pg 645 Pg 646 Pg 647 Pg 648 Pg 649 Pg 650 Pg 651 Pg 652 Pg 653 Pg 654
