
AllQuestion and Answers: Page 645
Question Number 155524 Answers: 0 Comments: 1
Question Number 155527 Answers: 2 Comments: 0
Question Number 155510 Answers: 1 Comments: 0

Question Number 155506 Answers: 1 Comments: 0
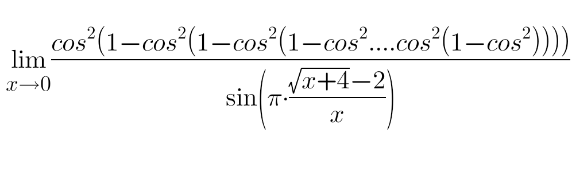
Question Number 155500 Answers: 2 Comments: 0
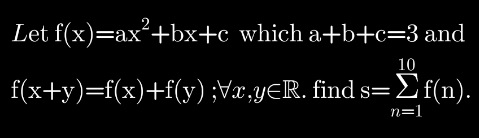
Question Number 155497 Answers: 1 Comments: 0

Question Number 155496 Answers: 1 Comments: 0
Question Number 155495 Answers: 1 Comments: 0
Question Number 155488 Answers: 1 Comments: 0

Question Number 155481 Answers: 1 Comments: 0
Question Number 155480 Answers: 1 Comments: 0
Question Number 155479 Answers: 1 Comments: 5
Question Number 155478 Answers: 1 Comments: 0
Question Number 155477 Answers: 1 Comments: 0

Question Number 155512 Answers: 1 Comments: 0
Question Number 155466 Answers: 2 Comments: 2
Question Number 155465 Answers: 1 Comments: 0
Question Number 155462 Answers: 0 Comments: 0

Question Number 155461 Answers: 0 Comments: 0

Question Number 155450 Answers: 2 Comments: 0
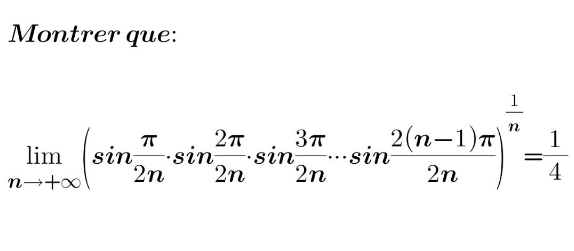
Question Number 155438 Answers: 0 Comments: 0

Question Number 155436 Answers: 0 Comments: 0
Question Number 155428 Answers: 2 Comments: 0
Question Number 155426 Answers: 1 Comments: 2

Question Number 155420 Answers: 1 Comments: 0
Question Number 155400 Answers: 0 Comments: 1
Pg 640 Pg 641 Pg 642 Pg 643 Pg 644 Pg 645 Pg 646 Pg 647 Pg 648 Pg 649
