Question and Answers Forum

AllQuestion and Answers: Page 642

Question Number 154200 Answers: 1 Comments: 0

g(((x−1)/(x+1)))=((7x+3)/(x+1)) and f(x^2 −2x+3)=3x^2 −6x+7 find (f+g)(x)=?

$${g}\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)=\frac{\mathrm{7}{x}+\mathrm{3}}{{x}+\mathrm{1}}\:\:{and}\:\:{f}\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{3}\right)=\mathrm{3}{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{7} \\ $$$${find}\:\:\left({f}+{g}\right)\left({x}\right)=?\:\:\: \\ $$

Question Number 154116 Answers: 0 Comments: 0

Question Number 154104 Answers: 3 Comments: 0

∫ e^(√x) dx =?

$$\:\:\int\:{e}^{\sqrt{{x}}} \:{dx}\:=? \\ $$

Question Number 154103 Answers: 2 Comments: 2

si w est une racine cubique de 1 different de 1,alors: (1+w−w^2 )^7 =?

$${si}\:{w}\:{est}\:{une}\:{racine}\:{cubique}\:{de}\:\mathrm{1}\:{different}\:{de}\:\mathrm{1},{alors}: \\ $$$$\left(\mathrm{1}+{w}−{w}^{\mathrm{2}} \right)^{\mathrm{7}} =? \\ $$

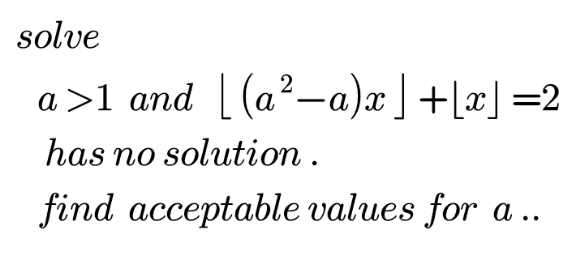
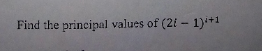
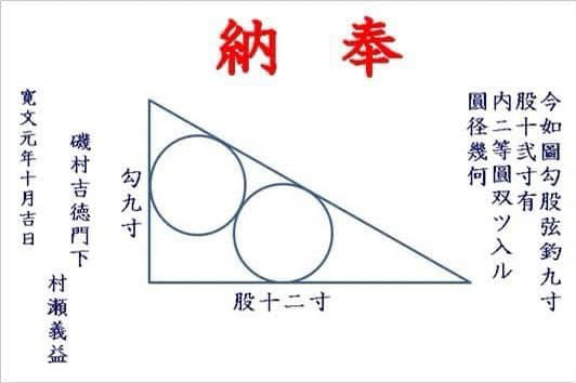
Question Number 154102 Answers: 0 Comments: 0

Question Number 154100 Answers: 1 Comments: 0

Question Number 154099 Answers: 1 Comments: 0

{ ((x^2 +y(√(xy)) = 72)),((y^2 +x(√(xy)) = 36)) :}

$$\:\begin{cases}{{x}^{\mathrm{2}} +{y}\sqrt{{xy}}\:=\:\mathrm{72}}\\{{y}^{\mathrm{2}} +{x}\sqrt{{xy}}\:=\:\mathrm{36}}\end{cases} \\ $$

Question Number 154088 Answers: 1 Comments: 1

Question Number 154087 Answers: 0 Comments: 0

Question Number 154085 Answers: 1 Comments: 1

Question Number 154081 Answers: 1 Comments: 0

lim_(x→∞) ((32x^5 −14x^4 +3))^(1/5) −((128x^7 +6x^6 −1))^(1/7) =?

$$\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\sqrt[{\mathrm{5}}]{\mathrm{32}{x}^{\mathrm{5}} −\mathrm{14}{x}^{\mathrm{4}} +\mathrm{3}}−\sqrt[{\mathrm{7}}]{\mathrm{128}{x}^{\mathrm{7}} +\mathrm{6}{x}^{\mathrm{6}} −\mathrm{1}}\:=? \\ $$

Question Number 154080 Answers: 1 Comments: 0

Ω =∫_0 ^( (π/2)) ln^2 (((1+sin t)/(1−sin t)))dt

$$\:\:\:\:\Omega\:=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \mathrm{ln}\:^{\mathrm{2}} \left(\frac{\mathrm{1}+\mathrm{sin}\:{t}}{\mathrm{1}−\mathrm{sin}\:{t}}\right){dt} \\ $$

Question Number 154078 Answers: 0 Comments: 1

Question Number 154068 Answers: 3 Comments: 3

Question Number 154065 Answers: 1 Comments: 0

Question Number 154064 Answers: 0 Comments: 0

Question Number 154062 Answers: 0 Comments: 0

Question Number 154059 Answers: 0 Comments: 0

Question Number 154058 Answers: 1 Comments: 0

Question Number 154052 Answers: 0 Comments: 0

Prove without any software ∫_( 2−(√3)) ^( 1) e^(−x^2 ) dx < (𝛑/6) and∫_( 1) ^( 2+(√3)) e^(−x^2 ) dx < (𝛑/6)

$$\mathrm{Prove}\:\mathrm{without}\:\mathrm{any}\:\mathrm{software} \\ $$$$\underset{\:\mathrm{2}−\sqrt{\mathrm{3}}} {\overset{\:\mathrm{1}} {\int}}\:\mathrm{e}^{−\boldsymbol{\mathrm{x}}^{\mathrm{2}} } \:\mathrm{dx}\:<\:\frac{\boldsymbol{\pi}}{\mathrm{6}}\:\:\mathrm{and}\underset{\:\mathrm{1}} {\overset{\:\mathrm{2}+\sqrt{\mathrm{3}}} {\int}}\mathrm{e}^{−\boldsymbol{\mathrm{x}}^{\mathrm{2}} } \:\mathrm{dx}\:<\:\frac{\boldsymbol{\pi}}{\mathrm{6}} \\ $$

Question Number 154051 Answers: 0 Comments: 0

let a≠b ; b≠c and c≠a find the minimum value of S = ∣(a/(b-c))∣ + ∣(b/(c-a))∣ + ∣(c/(a-b))∣

$$\mathrm{let}\:\:\mathrm{a}\neq\mathrm{b}\:;\:\mathrm{b}\neq\mathrm{c}\:\mathrm{and}\:\mathrm{c}\neq\mathrm{a} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of} \\ $$$$\boldsymbol{\mathrm{S}}\:=\:\mid\frac{\mathrm{a}}{\mathrm{b}-\mathrm{c}}\mid\:+\:\mid\frac{\mathrm{b}}{\mathrm{c}-\mathrm{a}}\mid\:+\:\mid\frac{\mathrm{c}}{\mathrm{a}-\mathrm{b}}\mid \\ $$

Question Number 154045 Answers: 2 Comments: 1

lim_(n→∞) (((Σ_(k=1) ^n (k^2 /(2k^2 −2nk+n^2 )))(Σ_(k=1) ^n (k^2 /(3k^2 −3nk+n^2 )))))^(1/n) =?

$$\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\sqrt[{{n}}]{\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{{k}^{\mathrm{2}} }{\mathrm{2}{k}^{\mathrm{2}} −\mathrm{2}{nk}+{n}^{\mathrm{2}} }\right)\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{{k}^{\mathrm{2}} }{\mathrm{3}{k}^{\mathrm{2}} −\mathrm{3}{nk}+{n}^{\mathrm{2}} }\right)}\:=? \\ $$

Question Number 154044 Answers: 0 Comments: 0

Question Number 154038 Answers: 0 Comments: 1

monster integral ∫_(−∞) ^( ∞) sin(x^2 )cos(x^3 ) dx

$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{monster}\:\mathrm{integral} \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\int_{−\infty} ^{\:\infty} \mathrm{sin}\left({x}^{\mathrm{2}} \right)\mathrm{cos}\left({x}^{\mathrm{3}} \right)\:{dx} \\ $$$$\: \\ $$$$\: \\ $$

Question Number 154037 Answers: 0 Comments: 0

Prove:: Σ_(n=−∞) ^(+∞) arctan (((sinh x)/(cosh n)))=πx

$$\mathrm{Prove}::\:\:\:\underset{\mathrm{n}=−\infty} {\overset{+\infty} {\sum}}\mathrm{arctan}\:\left(\frac{\mathrm{sinh}\:\mathrm{x}}{\mathrm{cosh}\:\mathrm{n}}\right)=\pi\mathrm{x} \\ $$

Question Number 154036 Answers: 3 Comments: 0

49(((x+5)/(x−2)))^2 +36(((x+5)/(x−1)))^2 = 85

$$\:\mathrm{49}\left(\frac{{x}+\mathrm{5}}{{x}−\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{36}\left(\frac{{x}+\mathrm{5}}{{x}−\mathrm{1}}\right)^{\mathrm{2}} =\:\mathrm{85} \\ $$

Pg 637 Pg 638 Pg 639 Pg 640 Pg 641 Pg 642 Pg 643 Pg 644 Pg 645 Pg 646

Contact: info@tinkutara.com