Question and Answers Forum

AllQuestion and Answers: Page 637

Question Number 154038 Answers: 0 Comments: 1

monster integral ∫_(−∞) ^( ∞) sin(x^2 )cos(x^3 ) dx

$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{monster}\:\mathrm{integral} \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\int_{−\infty} ^{\:\infty} \mathrm{sin}\left({x}^{\mathrm{2}} \right)\mathrm{cos}\left({x}^{\mathrm{3}} \right)\:{dx} \\ $$$$\: \\ $$$$\: \\ $$

Question Number 154037 Answers: 0 Comments: 0

Prove:: Σ_(n=−∞) ^(+∞) arctan (((sinh x)/(cosh n)))=πx

$$\mathrm{Prove}::\:\:\:\underset{\mathrm{n}=−\infty} {\overset{+\infty} {\sum}}\mathrm{arctan}\:\left(\frac{\mathrm{sinh}\:\mathrm{x}}{\mathrm{cosh}\:\mathrm{n}}\right)=\pi\mathrm{x} \\ $$

Question Number 154036 Answers: 3 Comments: 0

49(((x+5)/(x−2)))^2 +36(((x+5)/(x−1)))^2 = 85

$$\:\mathrm{49}\left(\frac{{x}+\mathrm{5}}{{x}−\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{36}\left(\frac{{x}+\mathrm{5}}{{x}−\mathrm{1}}\right)^{\mathrm{2}} =\:\mathrm{85} \\ $$

Question Number 154034 Answers: 1 Comments: 0

prove that n+x=(√(n^2 +x(√(n^2 +(x+n)(√(n^2 +(x+2n)(√(n^2 …)))))))) Ramanujan′s nested radikal

$${prove}\:{that}\: \\ $$$${n}+{x}=\sqrt{{n}^{\mathrm{2}} +{x}\sqrt{{n}^{\mathrm{2}} +\left({x}+{n}\right)\sqrt{{n}^{\mathrm{2}} +\left({x}+\mathrm{2}{n}\right)\sqrt{{n}^{\mathrm{2}} \ldots}}}} \\ $$$${Ramanujan}'{s}\:{nested}\:{radikal} \\ $$

Question Number 154022 Answers: 0 Comments: 0

An ANSWER on this forum is LUCKY if it receives a FEED BACK from the QUESTIONER!

$$ \\ $$$$\:\:\:\:\:\:\:\mathrm{An}\:\mathbb{ANSWER}\:\mathrm{on}\:\mathrm{this}\:\mathrm{forum} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{is}\:\:\mathbb{LUCKY} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{if}\:\mathrm{it}\:\mathrm{receives}\:\mathrm{a}\:\mathbb{FEED}\:\mathbb{BACK} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{from}\:\mathrm{the}\:\mathbb{QUESTIONER}! \\ $$$$ \\ $$

Question Number 154020 Answers: 2 Comments: 7

Question Number 154019 Answers: 0 Comments: 0

Question Number 154018 Answers: 0 Comments: 0

Question Number 154017 Answers: 0 Comments: 0

Question Number 154015 Answers: 0 Comments: 0

If x;y;z>0 then prove that: (x/(x^2 +yz)) + (y/(y^2 +zx)) + (z/(z^2 +xy)) ≤ ((x^2 +y^2 +z^2 )/(2xyz))

$$\mathrm{If}\:\:\mathrm{x};\mathrm{y};\mathrm{z}>\mathrm{0}\:\:\mathrm{then}\:\mathrm{prove}\:\mathrm{that}: \\ $$$$\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{yz}}\:+\:\frac{\mathrm{y}}{\mathrm{y}^{\mathrm{2}} +\mathrm{zx}}\:+\:\frac{\mathrm{z}}{\mathrm{z}^{\mathrm{2}} +\mathrm{xy}}\:\leqslant\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} }{\mathrm{2xyz}} \\ $$

Question Number 154013 Answers: 0 Comments: 0

Prove without any software ∫_( (1/2)) ^( ((√3)/2)) (1/x) log(1+2x^2 +x^4 )dx < (√7) - (√5)

$$\mathrm{Prove}\:\mathrm{without}\:\mathrm{any}\:\mathrm{software} \\ $$$$\underset{\:\frac{\mathrm{1}}{\mathrm{2}}} {\overset{\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} {\int}}\:\frac{\mathrm{1}}{\mathrm{x}}\:\mathrm{log}\left(\mathrm{1}+\mathrm{2x}^{\mathrm{2}} +\mathrm{x}^{\mathrm{4}} \right)\mathrm{dx}\:<\:\sqrt{\mathrm{7}}\:-\:\sqrt{\mathrm{5}} \\ $$

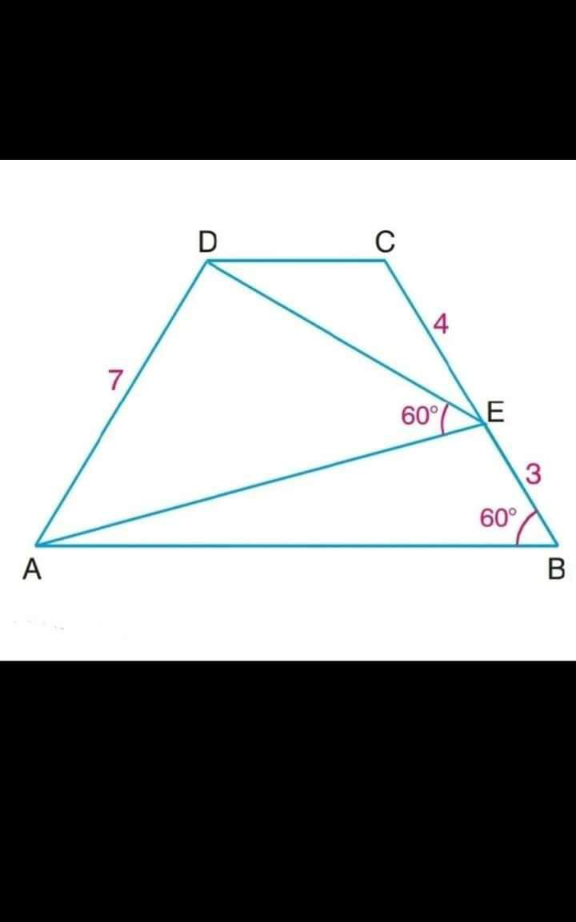
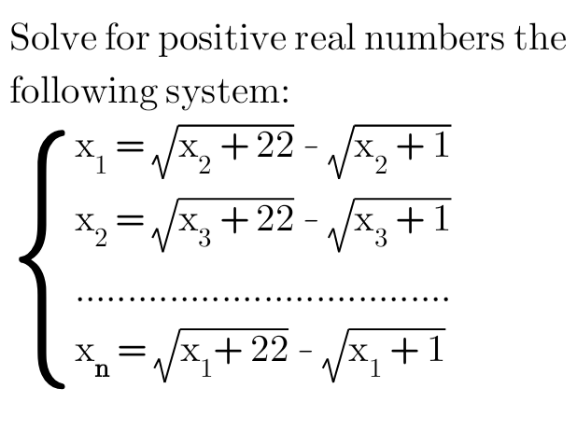
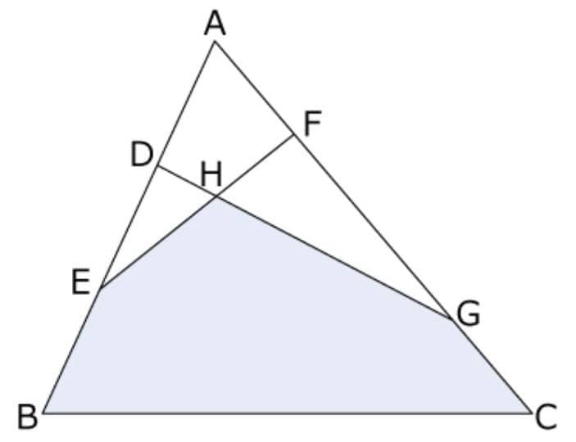
Question Number 154012 Answers: 1 Comments: 2

Determine all the perfect squares on form p^n + 1 where p is a prime number and n a positive integer.

$$\mathrm{Determine}\:\mathrm{all}\:\mathrm{the}\:\mathrm{perfect}\:\mathrm{squares}\:\mathrm{on} \\ $$$$\mathrm{form}\:\:\boldsymbol{\mathrm{p}}^{\boldsymbol{\mathrm{n}}} \:+\:\mathrm{1}\:\:\mathrm{where}\:\:\boldsymbol{\mathrm{p}}\:\:\mathrm{is}\:\mathrm{a}\:\mathrm{prime}\:\mathrm{number} \\ $$$$\mathrm{and}\:\:\boldsymbol{\mathrm{n}}\:\:\mathrm{a}\:\mathrm{positive}\:\mathrm{integer}. \\ $$

Question Number 154011 Answers: 0 Comments: 4

Ω =∫_( 0) ^( (𝛑/(12))) x(tanx + cotx) dx = ?

$$\Omega\:=\underset{\:\mathrm{0}} {\overset{\:\frac{\boldsymbol{\pi}}{\mathrm{12}}} {\int}}\mathrm{x}\left(\mathrm{tan}\boldsymbol{\mathrm{x}}\:+\:\mathrm{cot}\boldsymbol{\mathrm{x}}\right)\:\mathrm{dx}\:=\:? \\ $$

Question Number 153993 Answers: 1 Comments: 0

Given that ∫_0 ^( 12) f(x) dx=20, find the value of ∫_1 ^( 8) ((f(4 log_2 x))/x) dx.

$$\mathrm{Given}\:\mathrm{that}\:\int_{\mathrm{0}} ^{\:\mathrm{12}} {f}\left({x}\right)\:{dx}=\mathrm{20}, \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\int_{\mathrm{1}} ^{\:\mathrm{8}} \:\frac{{f}\left(\mathrm{4}\:\mathrm{log}_{\mathrm{2}} {x}\right)}{{x}}\:{dx}. \\ $$

Question Number 153989 Answers: 0 Comments: 0

find all functions f : R→R with the property that f(f(x) + 2y = 10x + f(f(y)-3x) holds for all a;b∈R

$$\mathrm{find}\:\mathrm{all}\:\mathrm{functions}\:\:\mathrm{f}\::\:\mathbb{R}\rightarrow\mathbb{R}\:\:\mathrm{with}\:\mathrm{the} \\ $$$$\mathrm{property}\:\mathrm{that} \\ $$$$\mathrm{f}\left(\mathrm{f}\left(\mathrm{x}\right)\:+\:\mathrm{2y}\:=\:\mathrm{10x}\:+\:\mathrm{f}\left(\mathrm{f}\left(\mathrm{y}\right)-\mathrm{3x}\right)\right. \\ $$$$\mathrm{holds}\:\mathrm{for}\:\mathrm{all}\:\:\mathrm{a};\mathrm{b}\in\mathbb{R} \\ $$

Question Number 153988 Answers: 1 Comments: 0

let a;b be positive real numbers such that a+b=2 prove that: (1/a^n ) + (1/b^n ) ≥ a^(n+1) + b^(n+1) ; ∀n∈N^∗

$$\mathrm{let}\:\:\mathrm{a};\mathrm{b}\:\:\mathrm{be}\:\mathrm{positive}\:\mathrm{real}\:\mathrm{numbers} \\ $$$$\mathrm{such}\:\mathrm{that}\:\:\mathrm{a}+\mathrm{b}=\mathrm{2}\:\:\mathrm{prove}\:\mathrm{that}: \\ $$$$\frac{\mathrm{1}}{\mathrm{a}^{\boldsymbol{\mathrm{n}}} }\:+\:\frac{\mathrm{1}}{\mathrm{b}^{\boldsymbol{\mathrm{n}}} }\:\geqslant\:\mathrm{a}^{\boldsymbol{\mathrm{n}}+\mathrm{1}} \:+\:\mathrm{b}^{\boldsymbol{\mathrm{n}}+\mathrm{1}} \:\:;\:\:\forall\mathrm{n}\in\mathbb{N}^{\ast} \\ $$

Question Number 154204 Answers: 2 Comments: 1

Question Number 153973 Answers: 2 Comments: 0

Question Number 153972 Answers: 2 Comments: 0

soit:f→x^3 +3x+1 alors:(f^(_1) )^(′′) (5)=?

$${soit}:{f}\rightarrow{x}^{\mathrm{3}} +\mathrm{3}{x}+\mathrm{1} \\ $$$${alors}:\left({f}^{\_\mathrm{1}} \right)^{''} \left(\mathrm{5}\right)=? \\ $$

Question Number 153965 Answers: 1 Comments: 0

If 3x^2 −2xy+y^2 =1, prove that (d^2 y/dx^2 )=(2/((x−y)^3 ))

$$\mathrm{If}\:\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}{xy}+{y}^{\mathrm{2}} =\mathrm{1},\:\mathrm{prove}\:\mathrm{that}\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{\mathrm{2}}{\left({x}−{y}\right)^{\mathrm{3}} } \\ $$

Question Number 153963 Answers: 2 Comments: 0

Given that f and g are differentiable functions such that f ′(x)=(1/( (√(1+(f(x))^2 )) )), and g=f^( −1) , find g′(x).

$$\mathrm{Given}\:\mathrm{that}\:{f}\:\mathrm{and}\:{g}\:\mathrm{are}\:\mathrm{differentiable} \\ $$$$\mathrm{functions}\:\mathrm{such}\:\mathrm{that}\:{f}\:'\left({x}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\left({f}\left({x}\right)\right)^{\mathrm{2}} }\:}, \\ $$$$\mathrm{and}\:{g}={f}^{\:−\mathrm{1}} \:,\:\mathrm{find}\:{g}'\left({x}\right). \\ $$

Question Number 153958 Answers: 4 Comments: 0

Question Number 153959 Answers: 1 Comments: 0

Question Number 153956 Answers: 2 Comments: 0

Max & min value of function f(x)=(√(6−x)) +(√(12+x)) .

$$\:{Max}\:\&\:{min}\:{value}\:{of}\:{function} \\ $$$$\:{f}\left({x}\right)=\sqrt{\mathrm{6}−{x}}\:+\sqrt{\mathrm{12}+{x}}\:. \\ $$

Question Number 153950 Answers: 1 Comments: 0

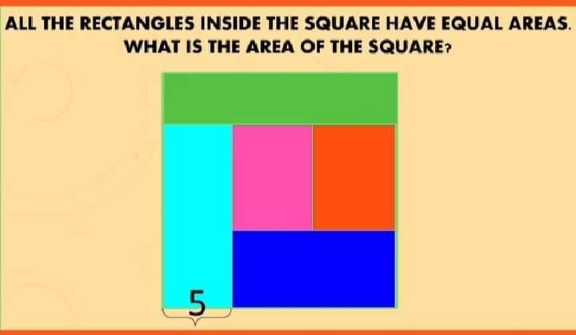
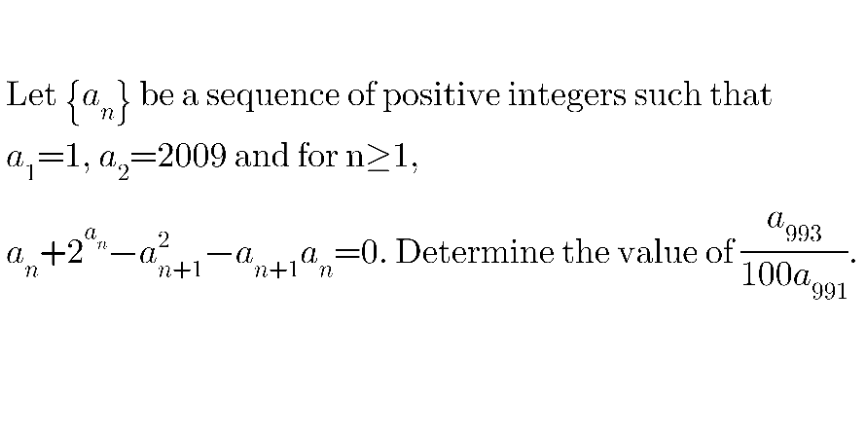
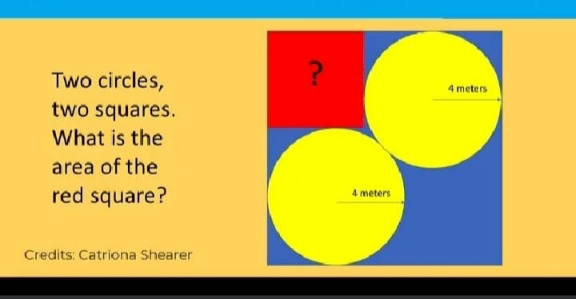
Question Number 153949 Answers: 1 Comments: 0

∫_0 ^( ∞) sin(x^2 )cos(x^3 )dx

$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} \:\mathrm{sin}\left({x}^{\mathrm{2}} \right)\mathrm{cos}\left({x}^{\mathrm{3}} \right){dx} \\ $$$$\: \\ $$

Pg 632 Pg 633 Pg 634 Pg 635 Pg 636 Pg 637 Pg 638 Pg 639 Pg 640 Pg 641

Contact: info@tinkutara.com