Question and Answers Forum

AllQuestion and Answers: Page 635

Question Number 154275 Answers: 0 Comments: 1

Question Number 154274 Answers: 0 Comments: 1

Solve the equation: x^2 ∙2^x (x^4 ∙4^x + 3∙15^x ) = 125^x - 27^x

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}: \\ $$$$\mathrm{x}^{\mathrm{2}} \centerdot\mathrm{2}^{\boldsymbol{\mathrm{x}}} \left(\mathrm{x}^{\mathrm{4}} \centerdot\mathrm{4}^{\boldsymbol{\mathrm{x}}} \:+\:\mathrm{3}\centerdot\mathrm{15}^{\boldsymbol{\mathrm{x}}} \right)\:=\:\mathrm{125}^{\boldsymbol{\mathrm{x}}} \:-\:\mathrm{27}^{\boldsymbol{\mathrm{x}}} \\ $$

Question Number 154273 Answers: 1 Comments: 0

Question Number 154270 Answers: 0 Comments: 0

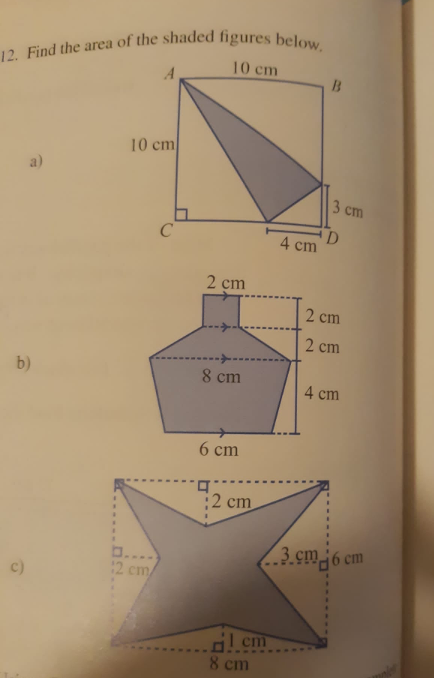
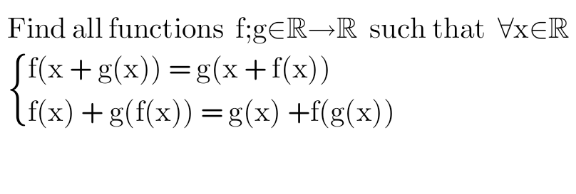
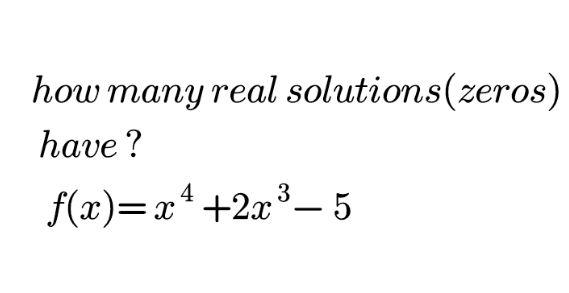
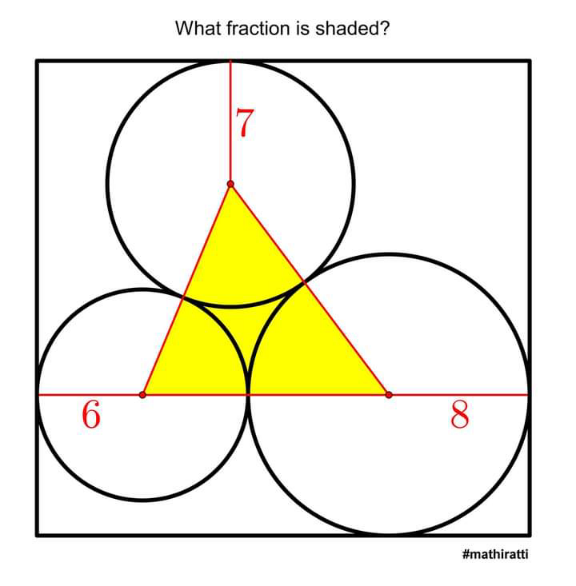
Question Number 154268 Answers: 0 Comments: 3

Question Number 154267 Answers: 0 Comments: 0

if x;y;z>0 and xy+yz+zx=3xyz then: (Σ_(cyc) (1/(x+y)))(Σ_(cyc) (1/(2x+y+z))) ≤ (9/8)

$$\mathrm{if}\:\:\mathrm{x};\mathrm{y};\mathrm{z}>\mathrm{0}\:\mathrm{and}\:\mathrm{xy}+\mathrm{yz}+\mathrm{zx}=\mathrm{3xyz}\:\:\mathrm{then}: \\ $$$$\left(\underset{\boldsymbol{\mathrm{cyc}}} {\sum}\:\frac{\mathrm{1}}{\mathrm{x}+\mathrm{y}}\right)\left(\underset{\boldsymbol{\mathrm{cyc}}} {\sum}\:\frac{\mathrm{1}}{\mathrm{2x}+\mathrm{y}+\mathrm{z}}\right)\:\leqslant\:\frac{\mathrm{9}}{\mathrm{8}} \\ $$

Question Number 154262 Answers: 1 Comments: 0

Question Number 154258 Answers: 1 Comments: 0

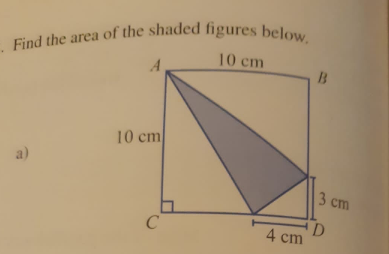
Question Number 154255 Answers: 1 Comments: 0

(5/(3^2 .7^2 ))+(9/(7^2 .11^2 ))+((13)/(11^2 .15^2 ))+…=?

$$\:\frac{\mathrm{5}}{\mathrm{3}^{\mathrm{2}} .\mathrm{7}^{\mathrm{2}} }+\frac{\mathrm{9}}{\mathrm{7}^{\mathrm{2}} .\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{13}}{\mathrm{11}^{\mathrm{2}} .\mathrm{15}^{\mathrm{2}} }+\ldots=? \\ $$

Question Number 154254 Answers: 0 Comments: 0

form a PDE from Z(x,y)=xf_1 (x−y)+2xf_2 (2x+y)

$${form}\:{a}\:{PDE}\:{from}\:{Z}\left({x},{y}\right)={xf}_{\mathrm{1}} \left({x}−{y}\right)+\mathrm{2}{xf}_{\mathrm{2}} \left(\mathrm{2}{x}+{y}\right) \\ $$

Question Number 154252 Answers: 0 Comments: 0

The {x_n } sequence is specified by the conditions { ((x_1 =1982)),((x_(n+1) =(1/(4−x_n )),n≥0)) :} find lim_(n→∞) x_n .

$$\:\:{The}\:\left\{{x}_{{n}} \right\}\:{sequence}\:{is}\:{specified} \\ $$$$\:{by}\:{the}\:{conditions}\: \\ $$$$\:\:\begin{cases}{{x}_{\mathrm{1}} =\mathrm{1982}}\\{{x}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{4}−{x}_{{n}} },{n}\geqslant\mathrm{0}}\end{cases} \\ $$$$\:{find}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}{x}_{{n}} . \\ $$

Question Number 154250 Answers: 0 Comments: 0

Question Number 154240 Answers: 1 Comments: 0

{ ((tg(a+b)=7)),((tg(a−b)=5)) :} tg(a)=? easy question

$$\begin{cases}{{tg}\left({a}+{b}\right)=\mathrm{7}}\\{{tg}\left({a}−{b}\right)=\mathrm{5}}\end{cases}\:\:{tg}\left({a}\right)=?\:\:\:{easy}\:{question} \\ $$

Question Number 154235 Answers: 1 Comments: 0

prove that: Im( ψ ( i ) )= (( 1)/( 2)) + (( π)/2) coth(π ) m.n

$$ \\ $$$$\:\:\:\:{prove}\:{that}: \\ $$$$\:\:\:\:\:\mathrm{I}{m}\left(\:\psi\:\left(\:{i}\:\right)\:\right)=\:\frac{\:\mathrm{1}}{\:\mathrm{2}}\:+\:\frac{\:\pi}{\mathrm{2}}\:{coth}\left(\pi\:\right) \\ $$$$\:\:\:\:\:\:\:\:{m}.{n} \\ $$

Question Number 154226 Answers: 0 Comments: 0

Given i(t)=25cos(ωt) ; u(t)=50[1+(ωt)^(2/(2!)) +(ωt)^(4/(4!)) +(ωt)^(6/(6!)) +...] . (1/T)∫_0 ^T u(t)×i(t)dt=??? choose the correct answer: a. 225 b. 425 c. 625 d. an other one

$${Given}\:{i}\left({t}\right)=\mathrm{25}{cos}\left(\omega{t}\right)\:; \\ $$$${u}\left({t}\right)=\mathrm{50}\left[\mathrm{1}+\left(\omega{t}\right)^{\frac{\mathrm{2}}{\mathrm{2}!}} +\left(\omega{t}\right)^{\frac{\mathrm{4}}{\mathrm{4}!}} +\left(\omega{t}\right)^{\frac{\mathrm{6}}{\mathrm{6}!}} +...\right]\:. \\ $$$$\frac{\mathrm{1}}{{T}}\underset{\mathrm{0}} {\overset{{T}} {\int}}{u}\left({t}\right)×{i}\left({t}\right){dt}=??? \\ $$$${choose}\:{the}\:{correct}\:{answer}: \\ $$$${a}.\:\mathrm{225} \\ $$$${b}.\:\mathrm{425} \\ $$$${c}.\:\mathrm{625} \\ $$$${d}.\:{an}\:{other}\:{one} \\ $$

Question Number 154223 Answers: 0 Comments: 0

∫_0 ^( 1) (x^( i+1) /(1−x)) dx = [−ln(1−x)x^( i+1) ]_0 ^( 1) + (1+i)∫_0 ^( 1) x^( i) ln (1−x )dx = (1+i ) ∫_0 ^( 1) Σ_(n=1) ^∞ (x^( n+i) /n)dx = (1+i )Σ(1/(n (n+i+1 )))= = Σ(1/(n )) −(1/(n+i+1)) = γ + ψ ( i+2 ) = γ + (1/(1+i)) +ψ (1+i) γ + ((1−i)/2) + (1/i) + ψ (i ) im = −(3/2) + (1/2) +(π/2) coth(π ) −1 +(π/2) tan h(π ) ..✓

$$ \\ $$$$\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{\:{i}+\mathrm{1}} }{\mathrm{1}−{x}}\:{dx}\:=\:\left[−{ln}\left(\mathrm{1}−{x}\right){x}^{\:{i}+\mathrm{1}} \right]_{\mathrm{0}} ^{\:\mathrm{1}} \\ $$$$\:\:\:+\:\left(\mathrm{1}+{i}\right)\int_{\mathrm{0}} ^{\:\mathrm{1}} {x}^{\:{i}} \:{ln}\:\left(\mathrm{1}−{x}\:\right){dx} \\ $$$$\:\:\:=\:\left(\mathrm{1}+{i}\:\right)\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{\:{n}+{i}} }{{n}}{dx} \\ $$$$\:=\:\:\left(\mathrm{1}+{i}\:\right)\Sigma\frac{\mathrm{1}}{{n}\:\left({n}+{i}+\mathrm{1}\:\right)}= \\ $$$$\:=\:\Sigma\frac{\mathrm{1}}{{n}\:}\:−\frac{\mathrm{1}}{{n}+{i}+\mathrm{1}}\:=\:\gamma\:+\:\psi\:\left(\:{i}+\mathrm{2}\:\right) \\ $$$$\:\:\:=\:\gamma\:+\:\frac{\mathrm{1}}{\mathrm{1}+{i}}\:+\psi\:\left(\mathrm{1}+{i}\right) \\ $$$$\:\:\:\:\:\gamma\:+\:\frac{\mathrm{1}−{i}}{\mathrm{2}}\:+\:\frac{\mathrm{1}}{{i}}\:+\:\psi\:\left({i}\:\right) \\ $$$$\:\:\:{im}\:=\:−\frac{\mathrm{3}}{\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\pi}{\mathrm{2}}\:{coth}\left(\pi\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{1}\:+\frac{\pi}{\mathrm{2}}\:{tan}\:{h}\left(\pi\:\right)\:..\checkmark \\ $$

Question Number 154225 Answers: 1 Comments: 1

In the expansion (1+(1/2)x)^n , the coefficient of x^m is (5/4) times the coefficient of x^(m+1) . a) Show that 5n−13m=8 b) If m and n are positive integers, such that m≤n, determine the smallest values of m and n.

$$\mathrm{In}\:\mathrm{the}\:\mathrm{expansion}\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}{x}\right)^{{n}} ,\:\mathrm{the}\:\mathrm{coefficient} \\ $$$$\mathrm{of}\:{x}^{{m}} \:\mathrm{is}\:\frac{\mathrm{5}}{\mathrm{4}}\:\mathrm{times}\:\mathrm{the}\:\mathrm{coefficient}\:\mathrm{of}\:{x}^{{m}+\mathrm{1}} . \\ $$$$\left.{a}\right)\:\mathrm{Show}\:\mathrm{that}\:\mathrm{5}{n}−\mathrm{13}{m}=\mathrm{8} \\ $$$$\left.{b}\right)\:\mathrm{If}\:{m}\:\mathrm{and}\:{n}\:\mathrm{are}\:\mathrm{positive}\:\mathrm{integers},\:\mathrm{such}\:\mathrm{that} \\ $$$$\:\:\:\:\:{m}\leqslant{n},\:\mathrm{determine}\:\mathrm{the}\:\mathrm{smallest}\:\mathrm{values}\:\mathrm{of} \\ $$$$\:\:\:\:\:{m}\:\mathrm{and}\:{n}. \\ $$

Question Number 154216 Answers: 3 Comments: 0

Solve the equation for reals ((cos^2 x−(1/5)sin^2 x+1)/(sin^2 x−(1/5)cos^2 x+1)) = 5tan^2 x

$${Solve}\:{the}\:{equation}\:{for}\:{reals}\: \\ $$$$\:\frac{\mathrm{cos}\:^{\mathrm{2}} {x}−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{sin}\:^{\mathrm{2}} {x}+\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} {x}−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{cos}\:^{\mathrm{2}} {x}+\mathrm{1}}\:=\:\mathrm{5tan}\:^{\mathrm{2}} {x}\: \\ $$

Question Number 154208 Answers: 0 Comments: 0

∵∴∵∴prove that ∫_0 ^∞ ∫_0 ^∞ ((log(1−e^(−x) )(yLi_2 (e^(−x−y) )+Li_3 (e^(−x−y) ))/(1−e^(x+y) ))e^(x+y) dxdy=((21)/8)ζ(6)+ζ^2 (3) ∵∴∵by MATH.AMIN∴∵∴

$$\because\therefore\because\therefore{prove}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} \frac{{log}\left(\mathrm{1}−{e}^{−{x}} \right)\left({yLi}_{\mathrm{2}} \left({e}^{−{x}−{y}} \right)+{Li}_{\mathrm{3}} \left({e}^{−{x}−{y}} \right)\right.}{\mathrm{1}−{e}^{{x}+{y}} }{e}^{{x}+{y}} {dxdy}=\frac{\mathrm{21}}{\mathrm{8}}\zeta\left(\mathrm{6}\right)+\zeta^{\mathrm{2}} \left(\mathrm{3}\right) \\ $$$$\because\therefore\because\boldsymbol{\mathrm{by}}\:\boldsymbol{\mathrm{MATH}}.\boldsymbol{\mathrm{AMIN}}\therefore\because\therefore \\ $$

Question Number 154202 Answers: 1 Comments: 0

𝛀 =∫_( 0) ^( ∞) ((ln∙(1 + x))/(x∙(x^2 + x + 1))) dx = ?

$$\boldsymbol{\Omega}\:\:=\underset{\:\mathrm{0}} {\overset{\:\infty} {\int}}\:\frac{\mathrm{ln}\centerdot\left(\mathrm{1}\:+\:\mathrm{x}\right)}{\mathrm{x}\centerdot\left(\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{x}\:+\:\mathrm{1}\right)}\:\mathrm{dx}\:=\:? \\ $$

Question Number 154194 Answers: 0 Comments: 1

Question Number 154195 Answers: 3 Comments: 0

∫((x+sinx)/(1+cosx))dx please,help me

$$\int\frac{{x}+{sinx}}{\mathrm{1}+{cosx}}{dx}\:\:\:\: \\ $$$${please},{help}\:{me} \\ $$

Question Number 154192 Answers: 1 Comments: 0

Ω :=∫_0 ^( 1) (( x.sin(ln(x)))/(1−x))dx method 1 Ω= Im[∫_0 ^( 1) (( x^( i+1) )/(1−x)) dx=Φ] Φ = ∫_0 ^( 1) (( x^( i+1) +x^( i+2) )/(1−x^( 2) ))dx =^(x^( 2) =t) (1/2)∫_0 ^( 1) (( t^( (i/2)) −t^((i+1)/2) )/(1−t))dt = (1/2) { ψ (1 +((i+1)/2))−ψ (1+(i/2))} = (1/2) { (2/(1+i)) + ψ ( ((1+i)/2) )−(2/i)−ψ ((i/2))} = ((−i)/(−1+i)) + (1/2) {ψ (((1+i)/2))−ψ((i/2) )} = −(1/2) +(i/(2 )) +(1/2) {ψ(((1+i)/2))−ψ((i/2))} Ω = Im (Φ )= (1/2) +(1/2) Im(ψ((1/2) +(i/2)))−(1/2) Im((i/2)) = (1/(2 )) { 1 +(π/2) tanh((π/2)) −1−(π/2) coth((π/2))} =(π/4) {((−1)/(sinh((π/2)).cosh((π/2))))}=((−π)/(2 sinh (π ))) ✓

Question Number 154186 Answers: 1 Comments: 0

Question Number 154177 Answers: 1 Comments: 2

Question Number 154175 Answers: 2 Comments: 1

Pg 630 Pg 631 Pg 632 Pg 633 Pg 634 Pg 635 Pg 636 Pg 637 Pg 638 Pg 639

Contact: info@tinkutara.com