
AllQuestion and Answers: Page 629
Question Number 157175 Answers: 2 Comments: 1

Question Number 157171 Answers: 1 Comments: 0
Question Number 157169 Answers: 1 Comments: 0

Question Number 157168 Answers: 1 Comments: 0
Question Number 157156 Answers: 1 Comments: 0
Question Number 157163 Answers: 1 Comments: 1
Question Number 157150 Answers: 0 Comments: 0
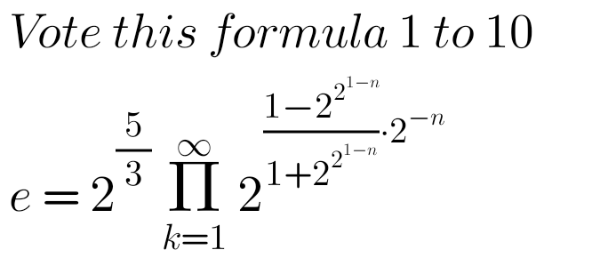
Question Number 157209 Answers: 2 Comments: 2

Question Number 157207 Answers: 0 Comments: 1
Question Number 157141 Answers: 1 Comments: 1
Question Number 157139 Answers: 1 Comments: 1
Question Number 157138 Answers: 0 Comments: 4
Question Number 157126 Answers: 0 Comments: 9
Question Number 157123 Answers: 0 Comments: 1
Question Number 157120 Answers: 2 Comments: 0
Question Number 157116 Answers: 1 Comments: 2
Question Number 157114 Answers: 0 Comments: 2

Question Number 157198 Answers: 1 Comments: 0
$$\mathrm{M}{ontrer}\:{que}\:{l}'{ensemble}\:{Q}\:{n}'{est}\:{ni}\:{ferme}\:{ni}\:{ouvert} \\ $$
Question Number 157197 Answers: 1 Comments: 0

Question Number 157196 Answers: 1 Comments: 0
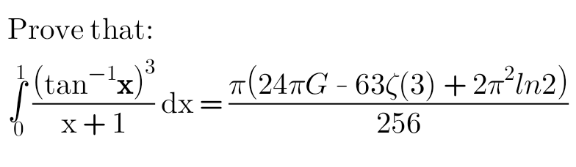
Question Number 157104 Answers: 2 Comments: 0
Question Number 157099 Answers: 0 Comments: 2

Question Number 157098 Answers: 1 Comments: 0
Question Number 157096 Answers: 1 Comments: 0
Question Number 157087 Answers: 0 Comments: 0
Question Number 157083 Answers: 0 Comments: 0

Pg 624 Pg 625 Pg 626 Pg 627 Pg 628 Pg 629 Pg 630 Pg 631 Pg 632 Pg 633
