
AllQuestion and Answers: Page 615
Question Number 157593 Answers: 0 Comments: 0
Question Number 157592 Answers: 0 Comments: 0
Question Number 157591 Answers: 1 Comments: 0
Question Number 157585 Answers: 1 Comments: 0
Question Number 157584 Answers: 3 Comments: 0
Question Number 157576 Answers: 1 Comments: 2

Question Number 157575 Answers: 1 Comments: 3
Question Number 157565 Answers: 0 Comments: 0

Question Number 157562 Answers: 2 Comments: 0

Question Number 157560 Answers: 0 Comments: 0

Question Number 157561 Answers: 0 Comments: 0
Question Number 157546 Answers: 1 Comments: 5
Question Number 157538 Answers: 1 Comments: 1

Question Number 157531 Answers: 2 Comments: 0

Question Number 157515 Answers: 0 Comments: 0
$$\:\:\:\:\:\int\:\frac{{x}\:\mathrm{sin}\:{x}}{\mathrm{16}{x}+\mathrm{9}}\:{dx}\: \\ $$
Question Number 157508 Answers: 0 Comments: 1

Question Number 157494 Answers: 1 Comments: 0

Question Number 157487 Answers: 2 Comments: 0
Question Number 157489 Answers: 2 Comments: 0
Question Number 157478 Answers: 0 Comments: 12
Question Number 157469 Answers: 1 Comments: 0
Question Number 157457 Answers: 3 Comments: 0
Question Number 157456 Answers: 4 Comments: 0
$$\:\int\:\mathrm{5}^{\mathrm{3}−\mathrm{2}{x}} \:{dx}\:=? \\ $$
Question Number 157455 Answers: 1 Comments: 0
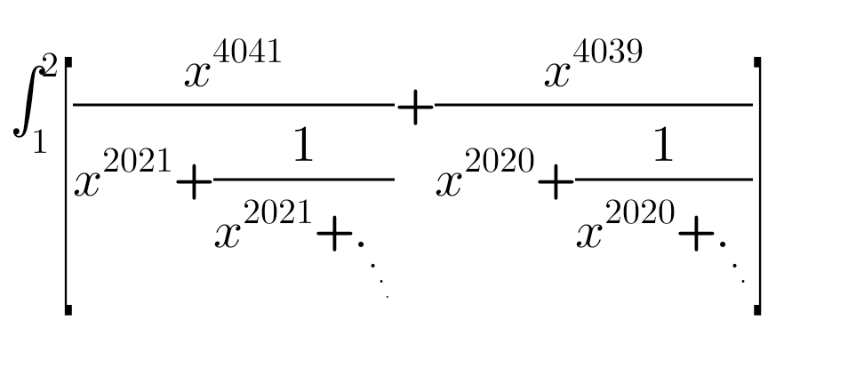
Question Number 157454 Answers: 2 Comments: 0
Question Number 157453 Answers: 1 Comments: 0

Pg 610 Pg 611 Pg 612 Pg 613 Pg 614 Pg 615 Pg 616 Pg 617 Pg 618 Pg 619
