Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 613

Question Number 152323 Answers: 1 Comments: 0

x^2 ∙y=(1/(18)) and x∙y^2 =(1/(12)) find (xy)^(−2) = ?

$$\mathrm{x}^{\mathrm{2}} \centerdot\mathrm{y}=\frac{\mathrm{1}}{\mathrm{18}}\:\:\mathrm{and}\:\:\mathrm{x}\centerdot\mathrm{y}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{12}} \\ $$$$\mathrm{find}\:\:\left(\mathrm{xy}\right)^{−\mathrm{2}} \:=\:? \\ $$

Question Number 152326 Answers: 1 Comments: 1

∫(√((1 + sinx)/(cosx))) dx = ?

$$\int\sqrt{\frac{\mathrm{1}\:+\:\mathrm{sin}\boldsymbol{\mathrm{x}}}{\mathrm{cos}\boldsymbol{\mathrm{x}}}}\:\mathrm{dx}\:=\:? \\ $$

Question Number 152321 Answers: 0 Comments: 0

Question Number 152314 Answers: 1 Comments: 0

Question Number 152310 Answers: 4 Comments: 0

Question Number 152299 Answers: 1 Comments: 4

Question Number 152291 Answers: 1 Comments: 0

∫ (dx/(cos x+cosec x)) =?

$$\:\int\:\frac{{dx}}{\mathrm{cos}\:{x}+\mathrm{cosec}\:{x}}\:=? \\ $$

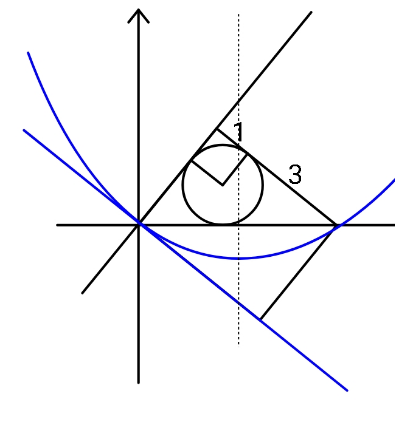
Question Number 152287 Answers: 2 Comments: 0

lim_(x→0) (1−tan^2 x)^(6/(sin^2 x)) =?

$$\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}\right)^{\frac{\mathrm{6}}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}} \:=? \\ $$

Question Number 152281 Answers: 1 Comments: 0

Find a triple of rational numbers (a,b,c) such that (((2)^(1/3) −1))^(1/3) = (a)^(1/3) +(b)^(1/3) + (c)^(1/3)

$$\mathrm{Find}\:\mathrm{a}\:\mathrm{triple}\:\mathrm{of}\:\mathrm{rational}\: \\ $$$$\mathrm{numbers}\:\left(\mathrm{a},\mathrm{b},\mathrm{c}\right)\:\mathrm{such}\:\mathrm{that}\: \\ $$$$\:\sqrt[{\mathrm{3}}]{\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{a}}\:+\sqrt[{\mathrm{3}}]{\mathrm{b}}\:+\:\sqrt[{\mathrm{3}}]{\mathrm{c}}\: \\ $$

Question Number 152276 Answers: 1 Comments: 0

Prove that ∫_0 ^π ((xtan x)/(sec x+tan x))dx=(π^2 /2)−π

$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{xtan}\:\mathrm{x}}{\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}}\mathrm{dx}=\frac{\pi^{\mathrm{2}} }{\mathrm{2}}−\pi \\ $$

Question Number 152275 Answers: 2 Comments: 0

∫_0 ^(π/2) sin 2xlog( tan x)dx

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}\:\mathrm{2xlog}\left(\:\mathrm{tan}\:\mathrm{x}\right)\mathrm{dx} \\ $$

Question Number 152273 Answers: 1 Comments: 0

∫ ((tan θ+tan^3 θ)/(1+tan^3 θ))dθ

$$\int\:\frac{\mathrm{tan}\:\theta+\mathrm{tan}\:^{\mathrm{3}} \theta}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{3}} \theta}\mathrm{d}\theta \\ $$

Question Number 152271 Answers: 1 Comments: 0

∫(3x−2)(√(x^2 +x+1)) dx

$$\int\left(\mathrm{3x}−\mathrm{2}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\:\mathrm{dx} \\ $$

Question Number 152270 Answers: 2 Comments: 0

∫((5x+3)/( (√(x^2 +4x+10))))dx

$$\int\frac{\mathrm{5x}+\mathrm{3}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{10}}}\mathrm{dx} \\ $$

Question Number 152265 Answers: 1 Comments: 0

Σ_(k=1) ^n sin^(−1) ((((√k) - (√(k - 1)))/( (√(k(k + 1))))) = ?

$$\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\boldsymbol{\mathrm{n}}} {\sum}}\mathrm{sin}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{k}}\:-\:\sqrt{\mathrm{k}\:-\:\mathrm{1}}}{\:\sqrt{\mathrm{k}\left(\mathrm{k}\:+\:\mathrm{1}\right.}}\right)\:=\:? \\ $$

Question Number 152247 Answers: 3 Comments: 0

show that lim_(x→0) ((((ln(1+x))/x) −1)/x)=−(1/2)

$${show}\:{that}\:\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}\:−\mathrm{1}}{{x}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Question Number 152244 Answers: 0 Comments: 0

𝛗 := ∫_0 ^( ∞) (( cos (x ).cosh (x ))/(cosh (πx )))dx=?

$$ \\ $$$$\:\:\:\:\:\:\boldsymbol{\phi}\::=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:{cos}\:\left({x}\:\right).{cosh}\:\left({x}\:\right)}{{cosh}\:\left(\pi{x}\:\right)}{dx}=? \\ $$$$ \\ $$

Question Number 152241 Answers: 4 Comments: 0

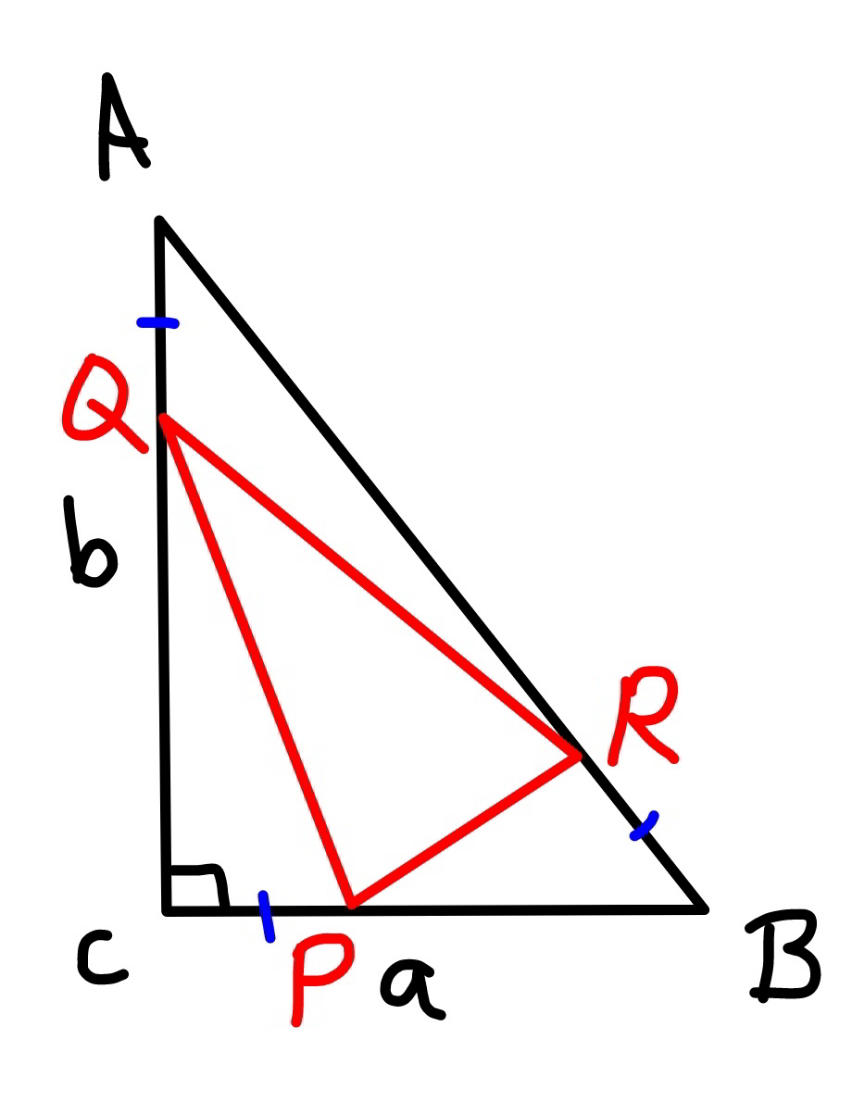
Question Number 152240 Answers: 1 Comments: 0

prove that.. csch (x)= (1/x) + Σ_(n=1) ^∞ ((2.(−1)^( n) x)/(n^( 2) π^( 2) + x^( 2) )) then find: Ω := ∫_0 ^( ∞) ((cosh (x )−(1/x))/x) dx=−ln(2)....■

$$ \\ $$$$\:\:{prove}\:{that}.. \\ $$$$\:\:\:{csch}\:\left({x}\right)=\:\frac{\mathrm{1}}{{x}}\:+\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}.\left(−\mathrm{1}\right)^{\:{n}} \:{x}}{{n}^{\:\mathrm{2}} \pi^{\:\mathrm{2}} +\:{x}^{\:\mathrm{2}} } \\ $$$$\:\:\:{then}\:{find}: \\ $$$$\:\:\:\:\Omega\::=\:\int_{\mathrm{0}} ^{\:\infty} \frac{{cosh}\:\left({x}\:\right)−\frac{\mathrm{1}}{{x}}}{{x}}\:{dx}=−{ln}\left(\mathrm{2}\right)....\blacksquare \\ $$

Question Number 152239 Answers: 0 Comments: 0

lim_(x→∞) (1 + a^n )^(1/n) [for a < 0, a > 0]

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}\:\:+\:\:\mathrm{a}^{\mathrm{n}} \right)^{\frac{\mathrm{1}}{\mathrm{n}}} \:\:\:\:\:\:\:\:\:\:\left[\mathrm{for}\:\:\:\:\:\:\:\mathrm{a}\:\:<\:\:\mathrm{0},\:\:\:\:\:\:\:\:\:\:\mathrm{a}\:\:>\:\:\mathrm{0}\right] \\ $$

Question Number 152226 Answers: 0 Comments: 1

16^(x^2 +y) + 16^(y^2 +x) = 1 ⇒ x;y=?

$$\mathrm{16}^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{y}}} \:+\:\mathrm{16}^{\boldsymbol{\mathrm{y}}^{\mathrm{2}} +\boldsymbol{\mathrm{x}}} \:=\:\mathrm{1}\:\:\Rightarrow\:\:\mathrm{x};\mathrm{y}=? \\ $$

Question Number 152211 Answers: 0 Comments: 1

lim_(x→0) (1/x^2 ) should the answer be ∞ or is it DNE. my main question is, when, lim_(x→a) f(x) = ∞ does it not exist? is it DNE?

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{should}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{be}\:\infty\:\mathrm{or}\:\mathrm{is}\:\mathrm{it}\:\mathrm{DNE}. \\ $$$$\mathrm{my}\:\mathrm{main}\:\mathrm{question}\:\mathrm{is}, \\ $$$$\mathrm{when}, \\ $$$$\underset{{x}\rightarrow\mathrm{a}} {\mathrm{lim}}\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\infty\: \\ $$$$\mathrm{does}\:\mathrm{it}\:\mathrm{not}\:\mathrm{exist}?\:\mathrm{is}\:\mathrm{it}\:\mathrm{DNE}? \\ $$

Question Number 152492 Answers: 1 Comments: 0

A particle is projected upwards with a velocity of 96ms^(−1) . In addition to being subject to gravity, it is acted on by a retardation of 16t, where t is the time from the start of the motion. What is the greatest height attained by the particle?

$$\:\mathrm{A}\:\mathrm{particle}\:\mathrm{is}\:\mathrm{projected}\:\mathrm{upwards}\:\mathrm{with} \\ $$$$\:\mathrm{a}\:\mathrm{velocity}\:\mathrm{of}\:\:\mathrm{96}{ms}^{−\mathrm{1}} .\:\mathrm{In}\:\mathrm{addition}\:\mathrm{to} \\ $$$$\:\mathrm{being}\:\mathrm{subject}\:\mathrm{to}\:\mathrm{gravity},\:\mathrm{it}\:\mathrm{is}\:\mathrm{acted}\:\mathrm{on} \\ $$$$\:\mathrm{by}\:\mathrm{a}\:\mathrm{retardation}\:\mathrm{of}\:\mathrm{16}{t},\:\mathrm{where}\:{t}\:\mathrm{is}\:\mathrm{the} \\ $$$$\:\mathrm{time}\:\mathrm{from}\:\mathrm{the}\:\mathrm{start}\:\mathrm{of}\:\mathrm{the}\:\mathrm{motion}. \\ $$$$\:\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{height}\:\mathrm{attained} \\ $$$$\:\mathrm{by}\:\mathrm{the}\:\mathrm{particle}? \\ $$

Question Number 152208 Answers: 1 Comments: 0

1.for ∀x>0.find the value of m to 1+log_5 (x^2 +1)≥log_5 (mx^2 +4x+m) verify ∀x.

$$\mathrm{1}.\mathrm{for}\:\forall\mathrm{x}>\mathrm{0}.\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\:\mathrm{m}\:\mathrm{to}\: \\ $$$$\mathrm{1}+\mathrm{log}_{\mathrm{5}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\geqslant\mathrm{log}_{\mathrm{5}} \left(\mathrm{mx}^{\mathrm{2}} +\mathrm{4x}+\mathrm{m}\right)\:\mathrm{verify}\:\forall\mathrm{x}. \\ $$

Question Number 152204 Answers: 3 Comments: 2

Question Number 152203 Answers: 0 Comments: 1

If x is real show that (2+i)^((1+3i)x) +(2−i)^((1−3i)x) is also real

$$\mathrm{If}\:\mathrm{x}\:\mathrm{is}\:\mathrm{real}\:\mathrm{show}\:\mathrm{that} \\ $$$$\left(\mathrm{2}+\mathrm{i}\right)^{\left(\mathrm{1}+\mathrm{3i}\right)\mathrm{x}} +\left(\mathrm{2}−\mathrm{i}\right)^{\left(\mathrm{1}−\mathrm{3i}\right)\mathrm{x}} \\ $$$$\mathrm{is}\:\mathrm{also}\:\mathrm{real} \\ $$

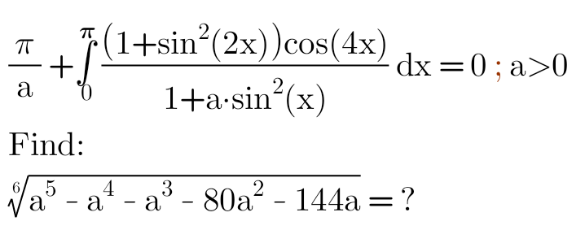
Pg 608 Pg 609 Pg 610 Pg 611 Pg 612 Pg 613 Pg 614 Pg 615 Pg 616 Pg 617

Terms of Service

Contact: info@tinkutara.com