
AllQuestion and Answers: Page 612
Question Number 158965 Answers: 2 Comments: 0
$$\:\int\:\frac{\sqrt{\mathrm{1}+{x}}}{\:\sqrt{{x}}\:+\mathrm{1}}\:{dx}\:=? \\ $$
Question Number 158964 Answers: 0 Comments: 1

Question Number 158945 Answers: 2 Comments: 0
Question Number 158941 Answers: 0 Comments: 1
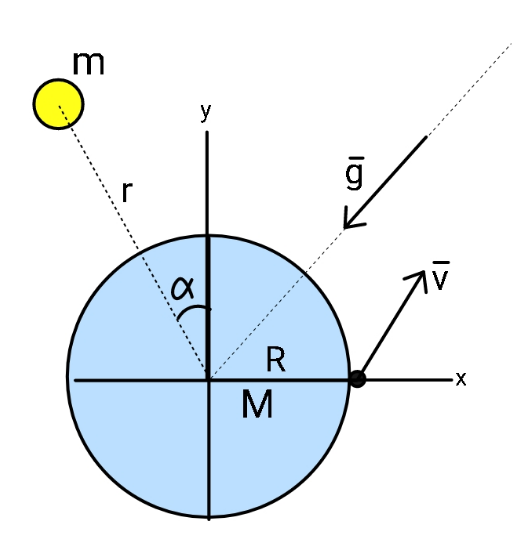
Question Number 158955 Answers: 1 Comments: 0

Question Number 158936 Answers: 0 Comments: 0
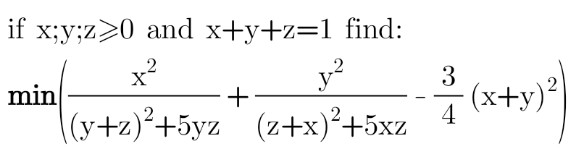
Question Number 158927 Answers: 2 Comments: 0

Question Number 158924 Answers: 1 Comments: 3
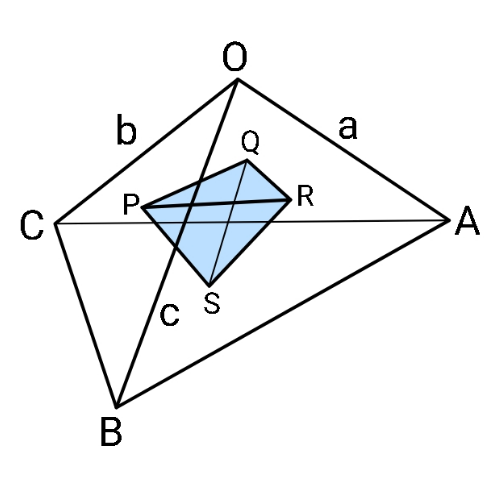
Question Number 158961 Answers: 1 Comments: 3
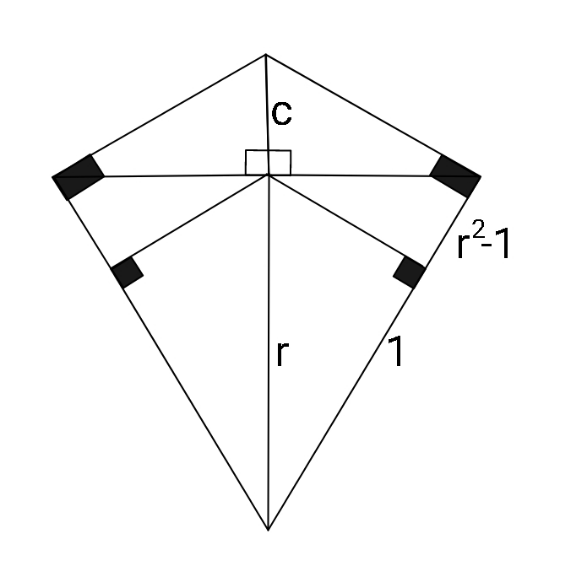
Question Number 158922 Answers: 0 Comments: 0
Question Number 158919 Answers: 1 Comments: 0

Question Number 158918 Answers: 0 Comments: 1

Question Number 158916 Answers: 0 Comments: 0

Question Number 158914 Answers: 0 Comments: 0
Question Number 158913 Answers: 0 Comments: 0

Question Number 158908 Answers: 1 Comments: 0

Question Number 158907 Answers: 1 Comments: 0
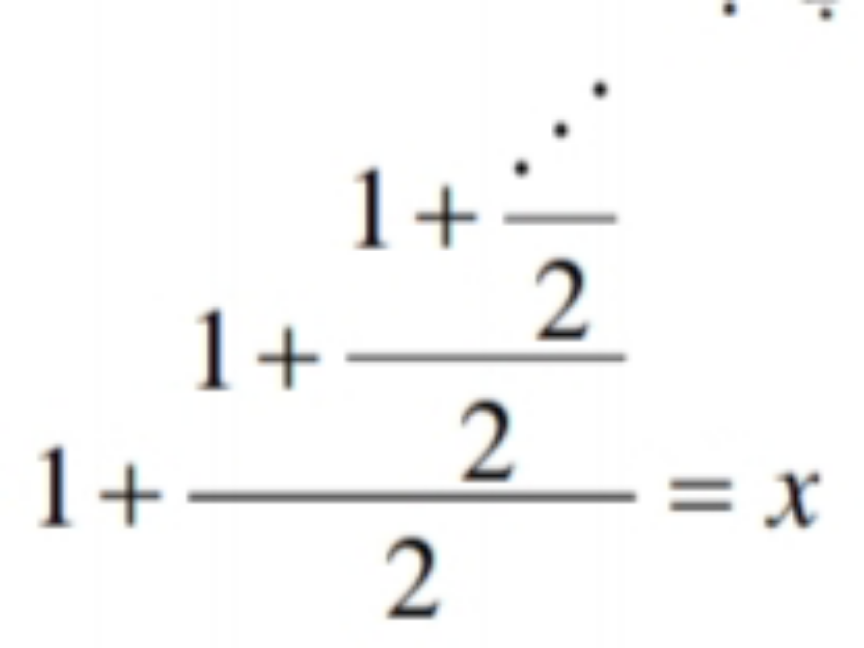
Question Number 158906 Answers: 1 Comments: 0
Question Number 158903 Answers: 0 Comments: 0
Question Number 158902 Answers: 0 Comments: 0
Question Number 158899 Answers: 1 Comments: 0
$$\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}= \\ $$
Question Number 158894 Answers: 0 Comments: 1
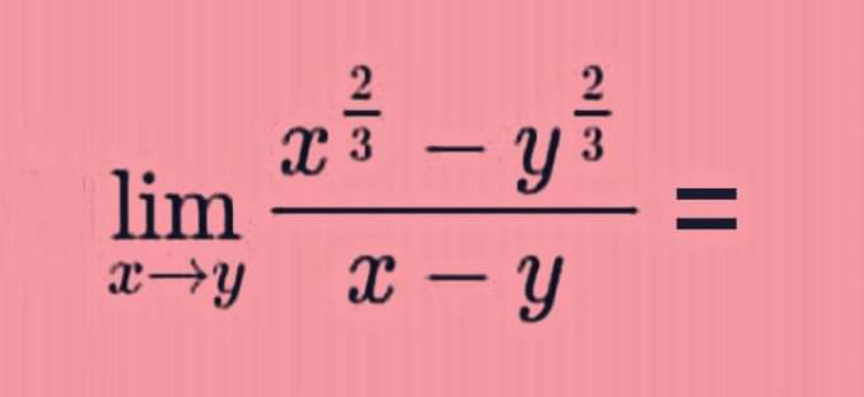
Question Number 158893 Answers: 1 Comments: 0

Question Number 158884 Answers: 1 Comments: 0
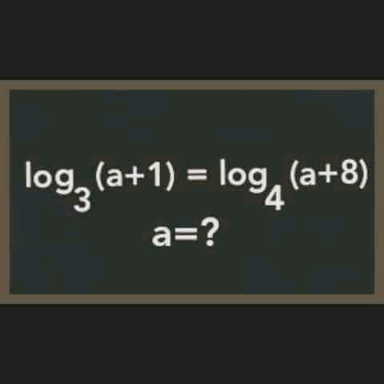
Question Number 158883 Answers: 1 Comments: 4

Question Number 158886 Answers: 0 Comments: 1

Pg 607 Pg 608 Pg 609 Pg 610 Pg 611 Pg 612 Pg 613 Pg 614 Pg 615 Pg 616
