Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 611

Question Number 159016 Answers: 0 Comments: 0

Question Number 159015 Answers: 1 Comments: 0

Question Number 159012 Answers: 0 Comments: 0

∫_0 ^( 1) (dx/(x^4 −x^2 +4))

$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{dx}}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{4}} \\ $$

Question Number 159011 Answers: 0 Comments: 0

G:N→N n→{_(n+1 si n est paire) ^(n si n est impair) g est−il inject ,surject ou biject?

$${G}:{N}\rightarrow{N} \\ $$$${n}\rightarrow\left\{_{{n}+\mathrm{1}\:{si}\:{n}\:{est}\:{paire}} ^{{n}\:\:{si}\:{n}\:{est}\:{impair}} \right. \\ $$$${g}\:{est}−{il}\:{inject}\:,{surject}\:{ou}\:{biject}? \\ $$

Question Number 159010 Answers: 0 Comments: 1

f:N→N n→{_(n+1 si impair) ^(n si paire) f est−il injective,surj ou bijec ?

$${f}:{N}\rightarrow{N} \\ $$$${n}\rightarrow\left\{_{{n}+\mathrm{1}\:{si}\:{impair}} ^{{n}\:\:{si}\:{paire}} \right. \\ $$$${f}\:{est}−{il}\:{injective},{surj}\:{ou}\:{bijec}\:? \\ $$

Question Number 159009 Answers: 0 Comments: 0

Question Number 159008 Answers: 1 Comments: 0

∫(6^x /(4^x +9^x ))dx=?

$$\int\frac{\mathrm{6}^{{x}} }{\mathrm{4}^{{x}} +\mathrm{9}^{{x}} }{dx}=? \\ $$

Question Number 159005 Answers: 2 Comments: 0

Question Number 159001 Answers: 0 Comments: 0

Question Number 159000 Answers: 0 Comments: 0

Question Number 158996 Answers: 0 Comments: 0

Prove that 2017^(2017) can be written as sum of eight perfect cubes.

$$\mathrm{Prove}\:\mathrm{that}\:\:\mathrm{2017}^{\mathrm{2017}} \:\:\mathrm{can}\:\mathrm{be}\:\mathrm{written} \\ $$$$\mathrm{as}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{eight}\:\mathrm{perfect}\:\mathrm{cubes}. \\ $$$$ \\ $$

Question Number 158995 Answers: 0 Comments: 1

A population of 15 items. 4 red, 6 black and 5 green. a sample of 4 items are selected. what is the probability that the sample contains 3 black and 1 green?

Question Number 158993 Answers: 0 Comments: 0

∫_0 ^1 ∫_0 ^1 xye^(x^2 y^2 ) dxdy=?

$$\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{\mathrm{xye}}^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}^{\mathrm{2}} } \boldsymbol{\mathrm{dxdy}}=? \\ $$

Question Number 158991 Answers: 0 Comments: 0

Question Number 158990 Answers: 0 Comments: 0

∫ ((sec x)/(sin x+csc x−1)) dx=?

$$\:\int\:\frac{\mathrm{sec}\:{x}}{\mathrm{sin}\:{x}+\mathrm{csc}\:{x}−\mathrm{1}}\:{dx}=? \\ $$

Question Number 158989 Answers: 0 Comments: 0

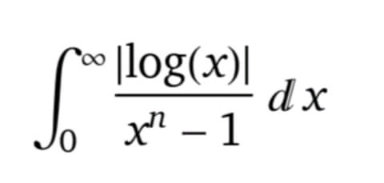
Question Number 158988 Answers: 2 Comments: 0

Question Number 158984 Answers: 0 Comments: 0

1. Prove by recurrence that so n ∈ N and θ ∈ R (cos (nθ)+isin (nθ)=cos (nθ)+isin (nθ) 2. Prove that U_(n+1) =(1/5)(U_n ^2 +6) and U_1 =(5/2), is decrease

$$\mathrm{1}.\:{Prove}\:{by}\:{recurrence}\:{that}\: \\ $$$${so}\:\:{n}\:\in\:{N}\:{and}\:\theta\:\in\: {R}\: \\ $$$$\left(\mathrm{cos}\:\left({n}\theta\right)+{i}\mathrm{sin}\:\left({n}\theta\right)=\mathrm{cos}\:\left({n}\theta\right)+{i}\mathrm{sin}\:\left({n}\theta\right)\right. \\ $$$$\mathrm{2}.\:{Prove}\:{that}\:{U}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{5}}\left({U}_{{n}} ^{\mathrm{2}} +\mathrm{6}\right)\:{and} \\ $$$${U}_{\mathrm{1}} =\frac{\mathrm{5}}{\mathrm{2}},\:{is}\:{decrease} \\ $$$$ \\ $$

Question Number 158983 Answers: 0 Comments: 0