
AllQuestion and Answers: Page 610
Question Number 160090 Answers: 0 Comments: 2
Question Number 159125 Answers: 0 Comments: 3
Question Number 159106 Answers: 0 Comments: 0
Question Number 159099 Answers: 1 Comments: 0

Question Number 159097 Answers: 0 Comments: 0
Question Number 159092 Answers: 1 Comments: 0

Question Number 159087 Answers: 0 Comments: 0

Question Number 159086 Answers: 0 Comments: 0

Question Number 159085 Answers: 1 Comments: 0
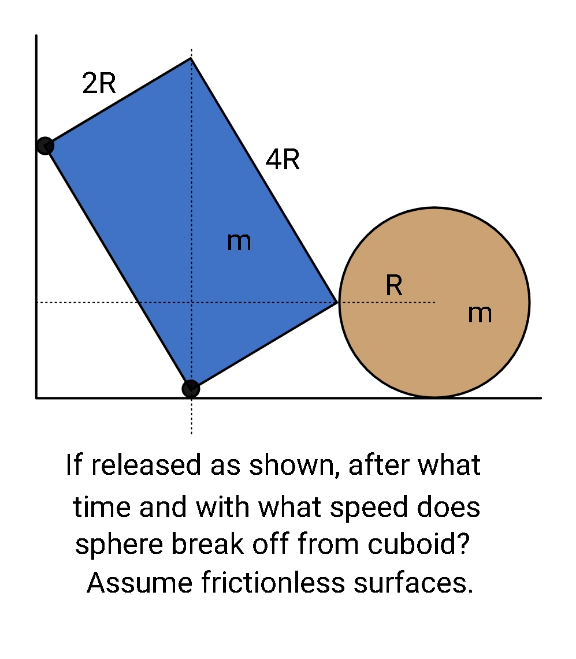
Question Number 159080 Answers: 1 Comments: 0
Question Number 159079 Answers: 1 Comments: 0
Question Number 159078 Answers: 0 Comments: 0
Question Number 159072 Answers: 0 Comments: 1

Question Number 159071 Answers: 1 Comments: 0
Question Number 159070 Answers: 1 Comments: 0
Question Number 159069 Answers: 0 Comments: 0

Question Number 159066 Answers: 0 Comments: 1
$$\mathrm{16}/\mathrm{4}\left(\mathrm{2}+\mathrm{2}\right)=? \\ $$
Question Number 159057 Answers: 1 Comments: 1
Question Number 159049 Answers: 2 Comments: 0
Question Number 159046 Answers: 1 Comments: 2

Question Number 159030 Answers: 1 Comments: 0
$$\:\left(\mathrm{arcsin}\:\left(\mathrm{cos}\:\mathrm{93}°\right)\right)^{\mathrm{2}} =? \\ $$
Question Number 159029 Answers: 0 Comments: 2
Question Number 159027 Answers: 0 Comments: 1
Question Number 159035 Answers: 0 Comments: 12

Question Number 159021 Answers: 1 Comments: 0
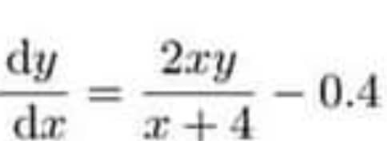
Question Number 159034 Answers: 1 Comments: 0
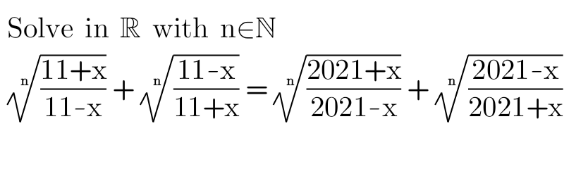
Pg 605 Pg 606 Pg 607 Pg 608 Pg 609 Pg 610 Pg 611 Pg 612 Pg 613 Pg 614
