Question and Answers Forum

AllQuestion and Answers: Page 609

Question Number 151461 Answers: 1 Comments: 0

∫((xdx)/(x^4 +4x^2 +5))

$$\int\frac{\mathrm{xdx}}{\mathrm{x}^{\mathrm{4}} +\mathrm{4x}^{\mathrm{2}} +\mathrm{5}} \\ $$

Question Number 151460 Answers: 1 Comments: 0

if f(x) = x^2 - 2x + 2 and g(x) = (√x) + 1 find [ f o g ] (x) = ?

$$\mathrm{if}\:\:\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{x}^{\mathrm{2}} \:-\:\mathrm{2x}\:+\:\mathrm{2} \\ $$$$\mathrm{and}\:\:\mathrm{g}\left(\mathrm{x}\right)\:=\:\sqrt{\mathrm{x}}\:+\:\mathrm{1} \\ $$$$\mathrm{find}\:\:\:\left[\:\mathrm{f}\:{o}\:\mathrm{g}\:\right]\:\left(\mathrm{x}\right)\:=\:? \\ $$

Question Number 151454 Answers: 0 Comments: 2

when a die is rolled 42 times it is so happened that a face having the digit i times occured 2i times. then find the mean deviation from the mean of this discrete frequency distribution. ans is ((80)/(63)) sol pls

$${when}\:{a}\:{die}\:{is}\:{rolled}\:\mathrm{42}\:{times}\:{it}\:{is}\:{so} \\ $$$${happened}\:{that}\:{a}\:{face}\:{having}\:{the}\:{digit}\:{i} \\ $$$${times}\:{occured}\:\mathrm{2}{i}\:{times}.\:{then}\:{find}\:{the} \\ $$$${mean}\:{deviation}\:{from}\:{the}\:{mean}\:{of}\:{this} \\ $$$${discrete}\:{frequency}\:{distribution}. \\ $$$${ans}\:{is}\:\frac{\mathrm{80}}{\mathrm{63}} \\ $$$${sol}\:{pls} \\ $$

Question Number 151453 Answers: 0 Comments: 7

find all continous functions f : R→R such that: f(x^2 + 1) = f((√(1 + x^4 ))) ; ∀x∈R

$$\mathrm{find}\:\mathrm{all}\:\mathrm{continous}\:\mathrm{functions}\:\mathrm{f}\::\:\mathbb{R}\rightarrow\mathbb{R} \\ $$$$\mathrm{such}\:\mathrm{that}: \\ $$$$\mathrm{f}\left(\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{1}\right)\:=\:\mathrm{f}\left(\sqrt{\mathrm{1}\:+\:\mathrm{x}^{\mathrm{4}} }\right)\:;\:\forall\mathrm{x}\in\mathbb{R} \\ $$

Question Number 151449 Answers: 2 Comments: 0

Ω =∫_( 0) ^( ∞) sin(x^2 ) dx = ?

$$\Omega\:=\underset{\:\mathrm{0}} {\overset{\:\infty} {\int}}\:\mathrm{sin}\left(\mathrm{x}^{\mathrm{2}} \right)\:\mathrm{dx}\:=\:? \\ $$

Question Number 151448 Answers: 1 Comments: 2

Prove that: Artimetric mean ≥ Geometric mean ((a + b)/2) ≥ (√(ab))

$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\boldsymbol{\mathrm{A}}\mathrm{rtimetric}\:\mathrm{mean}\:\geqslant\:\boldsymbol{\mathrm{G}}\mathrm{eometric}\:\mathrm{mean} \\ $$$$\frac{\mathrm{a}\:+\:\mathrm{b}}{\mathrm{2}}\:\geqslant\:\sqrt{\mathrm{ab}} \\ $$

Question Number 151447 Answers: 1 Comments: 0

prove that... I:= ∫_0 ^( ∞) (( ln (x ))/(1+ e^( x) )) dx= ((−1)/2) ln^( 2) (2) ..■

$$ \\ $$$$\:\:\:\:\:\:{prove}\:{that}... \\ $$$$\:\:\:\mathrm{I}:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:{ln}\:\left({x}\:\right)}{\mathrm{1}+\:{e}^{\:{x}} }\:{dx}=\:\frac{−\mathrm{1}}{\mathrm{2}}\:{ln}^{\:\mathrm{2}} \left(\mathrm{2}\right)\:..\blacksquare \\ $$

Question Number 151444 Answers: 2 Comments: 0

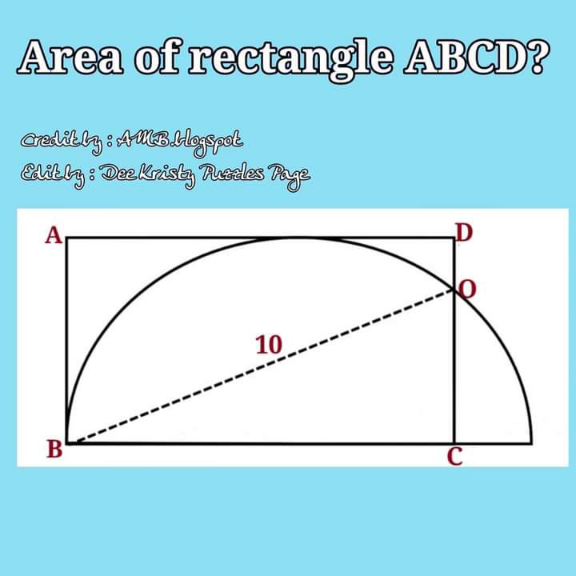
Question Number 151436 Answers: 0 Comments: 0

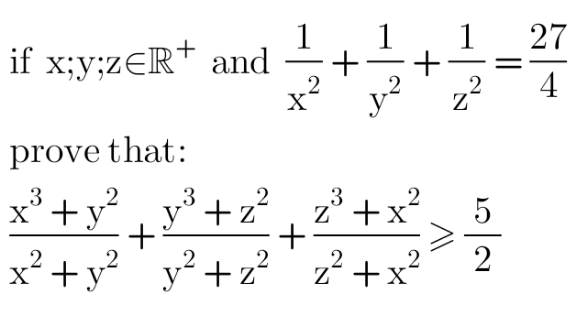
Question Number 151435 Answers: 1 Comments: 4

Question Number 151429 Answers: 1 Comments: 0

∫_0 ^π ((xdx)/((a^2 cos^2 x+b^2 sin^2 x)^2 ))

$$\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{xdx}}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \mathrm{x}+\mathrm{b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} } \\ $$

Question Number 151428 Answers: 1 Comments: 0

∫((x+2)/((x^2 +3x+3)(√(x+1))))dx

$$\int\frac{\mathrm{x}+\mathrm{2}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{3}\right)\sqrt{\mathrm{x}+\mathrm{1}}}\mathrm{dx} \\ $$$$ \\ $$

Question Number 151426 Answers: 3 Comments: 0

Express (1/(5×9)) in partial fraction

$$\mathrm{Express}\:\frac{\mathrm{1}}{\mathrm{5}×\mathrm{9}}\:\mathrm{in}\:\mathrm{partial}\:\mathrm{fraction} \\ $$

Question Number 151425 Answers: 2 Comments: 0

∫_0 ^(π/2) (dx/((cos x+(√3) sin x)^2 ))dx=(1/( (√3)))

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{dx}}{\left(\mathrm{cos}\:\mathrm{x}+\sqrt{\mathrm{3}}\:\mathrm{sin}\:\mathrm{x}\right)^{\mathrm{2}} }\mathrm{dx}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$

Question Number 151423 Answers: 1 Comments: 0

∫_0 ^(π/2) (dx/(1+tan^5 x))

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{dx}}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{5}} \mathrm{x}} \\ $$

Question Number 151421 Answers: 2 Comments: 2

∫_0 ^(π/4) log (1+tan x)dx

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{log}\:\left(\mathrm{1}+\mathrm{tan}\:\mathrm{x}\right)\mathrm{dx} \\ $$

Question Number 151418 Answers: 1 Comments: 0

Find the last three digits: 49^(303) ∙ 3993^(202) ∙ 39^(606)

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{last}\:\mathrm{three}\:\mathrm{digits}: \\ $$$$\mathrm{49}^{\mathrm{303}} \:\centerdot\:\mathrm{3993}^{\mathrm{202}} \:\centerdot\:\mathrm{39}^{\mathrm{606}} \\ $$

Question Number 151415 Answers: 0 Comments: 0

∫_0 ^∞ ((ln(x)arctg(x))/(x(x^2 +1)))dx

$$\int_{\mathrm{0}} ^{\infty} \frac{{ln}\left({x}\right){arctg}\left({x}\right)}{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx} \\ $$

Question Number 151404 Answers: 1 Comments: 1

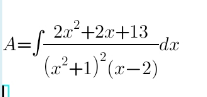
Question Number 151403 Answers: 0 Comments: 5

x^3 =3^x how do i pls use lambert to find x=3

$$\:{x}^{\mathrm{3}} =\mathrm{3}^{{x}} \\ $$$${how}\:{do}\:{i}\:{pls}\:{use}\:{lambert}\:{to}\: \\ $$$$\:{find}\:{x}=\mathrm{3} \\ $$

Question Number 151401 Answers: 1 Comments: 1

Question Number 151393 Answers: 2 Comments: 0

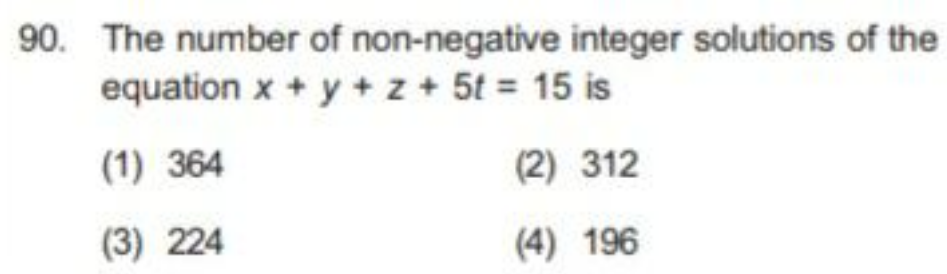
Question Number 151391 Answers: 1 Comments: 0

if a;b∈R and (a^2 +1)(b^2 +1)+9=6(a+b) find a^2 +b^2 =?

$$\mathrm{if}\:\:\mathrm{a};\mathrm{b}\in\mathbb{R}\:\:\mathrm{and} \\ $$$$\left(\mathrm{a}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{b}^{\mathrm{2}} +\mathrm{1}\right)+\mathrm{9}=\mathrm{6}\left(\mathrm{a}+\mathrm{b}\right) \\ $$$$\mathrm{find}\:\:\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} =? \\ $$

Question Number 151383 Answers: 1 Comments: 1

if x;y>0 peove that: (2/3) ∙ (2/((1/x)+(1/y))) + (1/3) ∙ (√((x^2 +y^2 )/2)) ≥ xy

$$\mathrm{if}\:\:\mathrm{x};\mathrm{y}>\mathrm{0}\:\:\mathrm{peove}\:\mathrm{that}: \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\:\centerdot\:\frac{\mathrm{2}}{\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{y}}}\:+\:\frac{\mathrm{1}}{\mathrm{3}}\:\centerdot\:\sqrt{\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }{\mathrm{2}}}\:\geqslant\:\mathrm{xy} \\ $$

Question Number 151377 Answers: 0 Comments: 2

the equation (y+13)(y+a) has no linear term. find value of a? what is means of no linear term. please expkain?

Question Number 151376 Answers: 0 Comments: 0

∫ ((x^8 +1)/( (√(x^9 −2x^8 +1)))) dx ?

$$\:\:\:\:\int\:\frac{\mathrm{x}^{\mathrm{8}} +\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{9}} −\mathrm{2x}^{\mathrm{8}} +\mathrm{1}}}\:\mathrm{dx}\:?\: \\ $$

Pg 604 Pg 605 Pg 606 Pg 607 Pg 608 Pg 609 Pg 610 Pg 611 Pg 612 Pg 613

Contact: info@tinkutara.com