
AllQuestion and Answers: Page 604
Question Number 159690 Answers: 1 Comments: 0

Question Number 159683 Answers: 2 Comments: 1
$$\mathrm{2}\:\leqslant\:\mid\boldsymbol{{x}}−\mathrm{2}\mid\:\leqslant\:\mathrm{6} \\ $$
Question Number 159682 Answers: 3 Comments: 0
Question Number 159681 Answers: 1 Comments: 0
Question Number 159680 Answers: 0 Comments: 2
Question Number 159675 Answers: 1 Comments: 2
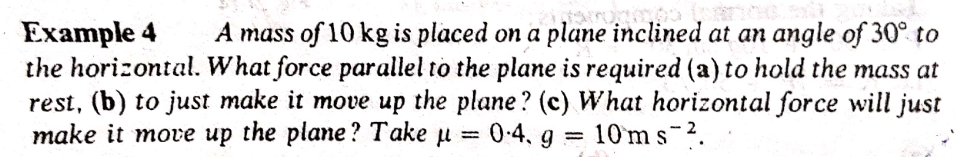
Question Number 159671 Answers: 1 Comments: 0
Question Number 159670 Answers: 1 Comments: 0

Question Number 159669 Answers: 1 Comments: 0
Question Number 159668 Answers: 0 Comments: 0
Question Number 159664 Answers: 0 Comments: 2
Question Number 159663 Answers: 0 Comments: 0
Question Number 159654 Answers: 0 Comments: 0
Question Number 159653 Answers: 1 Comments: 0
Question Number 159648 Answers: 2 Comments: 0
Question Number 159646 Answers: 1 Comments: 0
Question Number 159645 Answers: 0 Comments: 0

Question Number 159642 Answers: 2 Comments: 1
Question Number 159641 Answers: 0 Comments: 1
Question Number 159639 Answers: 1 Comments: 0
Question Number 159638 Answers: 0 Comments: 0
Question Number 159635 Answers: 0 Comments: 1

Question Number 159621 Answers: 0 Comments: 1

Question Number 159613 Answers: 0 Comments: 5

Question Number 159611 Answers: 2 Comments: 0
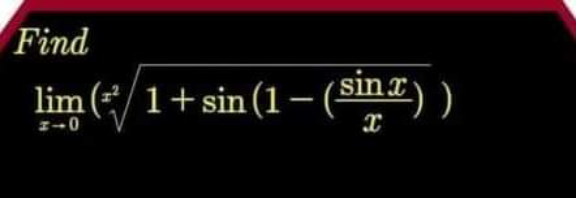
Question Number 159612 Answers: 2 Comments: 0
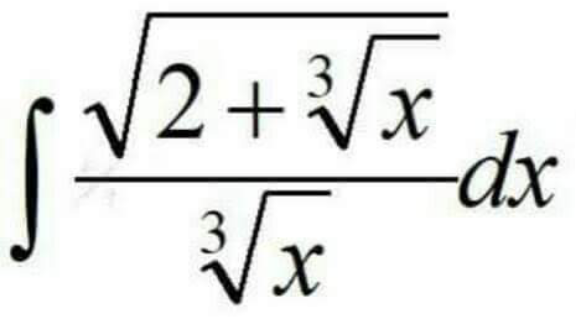
Pg 599 Pg 600 Pg 601 Pg 602 Pg 603 Pg 604 Pg 605 Pg 606 Pg 607 Pg 608
