Question and Answers Forum

AllQuestion and Answers: Page 589

Question Number 160933 Answers: 1 Comments: 0

In the given equation below , applying the formula for the derivative of inverse trigonometric functions , what is the ′′u ′′ from the given function. y = cosec^(−1) [ sin (((1+sin x)/(cos x)))]

$$\:{In}\:{the}\:{given}\:{equation}\:{below}\:,\:{applying} \\ $$$${the}\:{formula}\:{for}\:{the}\:{derivative}\:{of} \\ $$$$\:{inverse}\:{trigonometric}\:{functions}\:, \\ $$$$\:{what}\:{is}\:{the}\:''{u}\:''\:{from}\:{the}\:{given}\:{function}. \\ $$$$\:{y}\:=\:\mathrm{cosec}^{−\mathrm{1}} \left[\:\mathrm{sin}\:\left(\frac{\mathrm{1}+\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}\right)\right] \\ $$

Question Number 160931 Answers: 1 Comments: 0

x = 2^(log _5 (x+3)) ; x=?

$$\:\:{x}\:=\:\mathrm{2}^{\mathrm{log}\:_{\mathrm{5}} \left({x}+\mathrm{3}\right)} \:;\:{x}=? \\ $$

Question Number 160928 Answers: 1 Comments: 0

calculate Ω = Σ_(n=1) ^∞ (( ζ ( 1+ n ) −1)/(n + 1)) =^? 1− γ −−−−−−−−−−−

$$ \\ $$$$\:\:\:\:\:\:\:{calculate} \\ $$$$ \\ $$$$\:\:\:\:\Omega\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\:\zeta\:\left(\:\mathrm{1}+\:{n}\:\right)\:−\mathrm{1}}{{n}\:+\:\mathrm{1}}\:\overset{?} {=}\:\mathrm{1}−\:\gamma\: \\ $$$$\:−−−−−−−−−−− \\ $$

Question Number 160924 Answers: 1 Comments: 1

Question Number 160923 Answers: 0 Comments: 1

{ (((x+y)^(2021) = z)),(((x+z)^(2021) = y)),(((y+z)^(2021) = x)) :} (x,y,z)=...

$$\:\:\begin{cases}{\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2021}} =\:\mathrm{z}}\\{\left(\mathrm{x}+\mathrm{z}\right)^{\mathrm{2021}} \:=\:\mathrm{y}}\\{\left(\mathrm{y}+\mathrm{z}\right)^{\mathrm{2021}} \:=\:\mathrm{x}}\end{cases} \\ $$$$\:\:\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)=... \\ $$

Question Number 160922 Answers: 1 Comments: 0

monter que (3+(√5))^n +(3−(√5))^(n ) est divisible par 2^n beson d′aide svp

$${monter}\:{que}\:\left(\mathrm{3}+\sqrt{\mathrm{5}}\right)^{{n}} +\left(\mathrm{3}−\sqrt{\mathrm{5}}\right)^{{n}\:} \\ $$$${est}\:{divisible}\:{par}\:\mathrm{2}^{{n}} \\ $$$${beson}\:{d}'{aide}\:{svp} \\ $$

Question Number 160921 Answers: 0 Comments: 0

Find: 𝛀 =∫_( 1) ^( 21) (dx/e^([2x + (1/4)]) ) ; [∗]-GIF

$$\mathrm{Find}: \\ $$$$\boldsymbol{\Omega}\:=\underset{\:\mathrm{1}} {\overset{\:\mathrm{21}} {\int}}\:\frac{\mathrm{dx}}{\boldsymbol{\mathrm{e}}^{\left[\mathrm{2}\boldsymbol{\mathrm{x}}\:+\:\frac{\mathrm{1}}{\mathrm{4}}\right]} }\:\:\:;\:\:\:\left[\ast\right]-\mathrm{GIF} \\ $$

Question Number 160917 Answers: 1 Comments: 0

Calculate a)lim_(x→+∞) (((x−1)/(x+1)))^x^2 b) lim_(x→0) ((2^(1/x) −1)/(2^(1/x) +1))

$${Calculate} \\ $$$$\left.{a}\right)\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)^{{x}^{\mathrm{2}} } \\ $$$$\left.{b}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}^{\frac{\mathrm{1}}{{x}}} −\mathrm{1}}{\mathrm{2}^{\frac{\mathrm{1}}{{x}}} +\mathrm{1}} \\ $$

Question Number 160912 Answers: 1 Comments: 0

lim_(x→0) ((tan (x+2)tan (2−x)−tan^2 (2))/(3x tan x)) =?

$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\left(\mathrm{x}+\mathrm{2}\right)\mathrm{tan}\:\left(\mathrm{2}−\mathrm{x}\right)−\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{3x}\:\mathrm{tan}\:\mathrm{x}}\:=? \\ $$

Question Number 160910 Answers: 1 Comments: 0

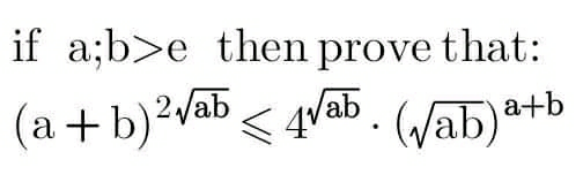
Question Number 160909 Answers: 2 Comments: 0

How many 3−digits number such that sum of its digits is 11 ?

$${How}\:\:{many}\:\:\mathrm{3}−{digits}\:\:{number}\:\:{such}\:\:{that}\:\:{sum}\:\:{of}\:\:{its}\:\:{digits}\:\:{is}\:\:\mathrm{11}\:? \\ $$

Question Number 160908 Answers: 0 Comments: 1

x,y,z ∈ R^+ Find the minimum value of this expression ((xyz)/((1+3x)(x+8y)(y+9z)(6+z)))

$${x},{y},{z}\:\:\in\:\:\mathbb{R}^{+} \\ $$$${Find}\:\:{the}\:\:{minimum}\:\:{value}\:\:{of}\:\:{this}\:\:{expression}\: \\ $$$$\:\:\:\:\:\:\frac{{xyz}}{\left(\mathrm{1}+\mathrm{3}{x}\right)\left({x}+\mathrm{8}{y}\right)\left({y}+\mathrm{9}{z}\right)\left(\mathrm{6}+{z}\right)}\:\: \\ $$$$ \\ $$

Question Number 160906 Answers: 0 Comments: 0

Question Number 160903 Answers: 2 Comments: 0

(1+x^2 )y ′= 2xy +(1+x^2 )^2

$$\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}\:'=\:\mathrm{2}{xy}\:+\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} \: \\ $$

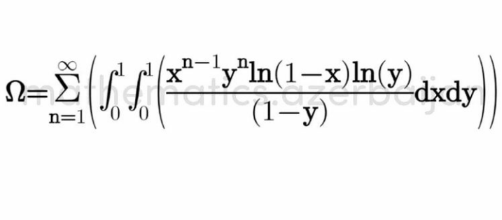
Question Number 160902 Answers: 1 Comments: 0

∫ (dx/( (√(sin^3 x)) (√(cos^5 x)))) =?

$$\:\:\int\:\frac{{dx}}{\:\sqrt{\mathrm{sin}\:^{\mathrm{3}} {x}}\:\sqrt{\mathrm{cos}\:^{\mathrm{5}} {x}}}\:=? \\ $$

Question Number 160900 Answers: 0 Comments: 2

Calculate 1) lim_(x→0) (((x+1)/(2x+1)))^x^2 lim_(x→a) (((sin x)/(sin a)))^(1/(x−a))

$${Calculate} \\ $$$$\left.\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{{x}+\mathrm{1}}{\mathrm{2}{x}+\mathrm{1}}\right)^{{x}^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:{a}}\right)^{\frac{\mathrm{1}}{{x}−{a}}} \\ $$

Question Number 160895 Answers: 1 Comments: 0

Prove that: ∫_( 0) ^( 1) ((ln(x))/(x^n + x^(n-1) + ... + 1)) dx = (1/n^2 ) [𝛙^((1)) ((2/n)) - 𝛙^((1)) ((1/n))]

$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\underset{\:\mathrm{0}} {\overset{\:\mathrm{1}} {\int}}\:\frac{\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{x}^{\boldsymbol{\mathrm{n}}} \:+\:\mathrm{x}^{\boldsymbol{\mathrm{n}}-\mathrm{1}} \:+\:...\:+\:\mathrm{1}}\:\mathrm{dx}\:=\:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\:\left[\boldsymbol{\psi}^{\left(\mathrm{1}\right)} \left(\frac{\mathrm{2}}{\mathrm{n}}\right)\:-\:\boldsymbol{\psi}^{\left(\mathrm{1}\right)} \left(\frac{\mathrm{1}}{\mathrm{n}}\right)\right] \\ $$

Question Number 160894 Answers: 1 Comments: 0

Question Number 160886 Answers: 0 Comments: 0

a_n is root of equation x^n +x=1,a_n ∈(0,1). Find lim_(n→∞) ((n−na_n −lnn)/(ln(lnn)))=?

$$\mathrm{a}_{\mathrm{n}} \:\mathrm{is}\:\mathrm{root}\:\mathrm{of}\:\mathrm{equation}\:\mathrm{x}^{\mathrm{n}} +\mathrm{x}=\mathrm{1},\mathrm{a}_{\mathrm{n}} \in\left(\mathrm{0},\mathrm{1}\right). \\ $$$$\mathrm{Find}\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{n}−\mathrm{na}_{\mathrm{n}} −\mathrm{lnn}}{\mathrm{ln}\left(\mathrm{lnn}\right)}=? \\ $$

Question Number 160885 Answers: 0 Comments: 0

lim_(n→∞) Σ_(k=1) ^n ((n+(1/k))/( (√(n^2 +k^2 ))))∙sin (1/n)=?

$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{n}+\frac{\mathrm{1}}{\mathrm{k}}}{\:\sqrt{\mathrm{n}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} }}\centerdot\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{n}}=? \\ $$

Question Number 160883 Answers: 1 Comments: 0

(√(x+1)) = ((x^2 −x−2 ((2x+1))^(1/3) )/( ((2x+1))^(1/3) −3 )) x ∈R

$$\:\sqrt{\mathrm{x}+\mathrm{1}}\:=\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{2}\:\sqrt[{\mathrm{3}}]{\mathrm{2x}+\mathrm{1}}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2x}+\mathrm{1}}\:−\mathrm{3}\:}\: \\ $$$$\:\mathrm{x}\:\in\mathbb{R}\: \\ $$

Question Number 160875 Answers: 1 Comments: 0

lim_(n→∞) ((5^n +7^n ))^(1/n) =?

$$\:\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\sqrt[{\mathrm{n}}]{\mathrm{5}^{\mathrm{n}} +\mathrm{7}^{\mathrm{n}} }\:=? \\ $$

Question Number 160873 Answers: 2 Comments: 0

Question Number 160871 Answers: 1 Comments: 0

(((2 (((2(√(13))+5)/( (√5)+2)))^(1/3) +2 (((2(√(13))−5)/( (√5)−2)))^(1/3) +1)^2 −1))^(1/6) =?

$$\:\:\sqrt[{\mathrm{6}}]{\left(\mathrm{2}\:\sqrt[{\mathrm{3}}]{\frac{\mathrm{2}\sqrt{\mathrm{13}}+\mathrm{5}}{\:\sqrt{\mathrm{5}}+\mathrm{2}}}\:+\mathrm{2}\:\sqrt[{\mathrm{3}}]{\frac{\mathrm{2}\sqrt{\mathrm{13}}−\mathrm{5}}{\:\sqrt{\mathrm{5}}−\mathrm{2}}}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}=? \\ $$

Question Number 160869 Answers: 0 Comments: 2

Find: 𝛀 =∫_( 0) ^( ∞) ((x ln (1 + x))/((x + 1)(x^2 + 1))) dx = ?

$$\mathrm{Find}: \\ $$$$\boldsymbol{\Omega}\:=\underset{\:\mathrm{0}} {\overset{\:\infty} {\int}}\:\frac{\mathrm{x}\:\mathrm{ln}\:\left(\mathrm{1}\:+\:\mathrm{x}\right)}{\left(\mathrm{x}\:+\:\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{1}\right)}\:\mathrm{dx}\:=\:? \\ $$

Question Number 160867 Answers: 0 Comments: 0

A piece of metal in the form of an equilateral triangle that has been subjected to hammering, and its circumference expands at a rate of 6 cm/s so that it remains preserved in its shape. The rate of change in its area when its side length is 12 cm

$$ \\ $$A piece of metal in the form of an equilateral triangle that has been subjected to hammering, and its circumference expands at a rate of 6 cm/s so that it remains preserved in its shape. The rate of change in its area when its side length is 12 cm

Pg 584 Pg 585 Pg 586 Pg 587 Pg 588 Pg 589 Pg 590 Pg 591 Pg 592 Pg 593

Contact: info@tinkutara.com