Question and Answers Forum

AllQuestion and Answers: Page 577

Question Number 161450 Answers: 0 Comments: 0

A ector field is given by v= (x^2 −y^2 +x)i−(2xy+y)j. Show that vector v is irrotational hence find the scalar potential

$$\mathrm{A}\: \mathrm{ector}\:\mathrm{field}\:\mathrm{is}\:\mathrm{given}\:\mathrm{by}\:\mathrm{v}= \\ $$$$\left(\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} +\mathrm{x}\right)\mathrm{i}−\left(\mathrm{2xy}+\mathrm{y}\right)\mathrm{j}.\:\mathrm{Show}\:\mathrm{that} \\ $$$$\mathrm{vector}\:\mathrm{v}\:\mathrm{is}\:\mathrm{irrotational}\:\mathrm{hence}\:\mathrm{find} \\ $$$$\:\mathrm{the}\:\mathrm{scalar}\:\mathrm{potential} \\ $$

Question Number 161444 Answers: 0 Comments: 2

Question Number 161443 Answers: 1 Comments: 0

Question Number 161442 Answers: 1 Comments: 0

Use the binomial theorem to write the first four terms of the expansion of (√(2+3x−x^2 ))

$$\mathrm{Use}\:\mathrm{the}\:\mathrm{binomial}\:\mathrm{theorem}\:\mathrm{to}\:\mathrm{write} \\ $$$$\mathrm{the}\:\mathrm{first}\:\mathrm{four}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{the}\:\mathrm{expansion} \\ $$$$\mathrm{of}\:\sqrt{\mathrm{2}+\mathrm{3}{x}−{x}^{\mathrm{2}} } \\ $$

Question Number 161439 Answers: 0 Comments: 1

Question Number 161437 Answers: 2 Comments: 0

lim_(x→0) ((((8x^2 −4x+1))^(1/(10)) +((7x^2 +3x+1))^(1/5) −2)/x) =?

$$\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{10}}]{\mathrm{8}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}}\:+\sqrt[{\mathrm{5}}]{\mathrm{7}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}}−\mathrm{2}}{{x}}\:=? \\ $$

Question Number 161433 Answers: 0 Comments: 0

if x;y;z>0 such that x+y+z=3 and 𝛌≥0 then prove that: (x/(y^3 +λy^2 )) + (y/(z^3 +λz^2 )) + (z/(x^3 +λx^2 )) ≥ (3/(λ+1))

$$\mathrm{if}\:\:\mathrm{x};\mathrm{y};\mathrm{z}>\mathrm{0}\:\:\mathrm{such}\:\mathrm{that}\:\:\mathrm{x}+\mathrm{y}+\mathrm{z}=\mathrm{3} \\ $$$$\mathrm{and}\:\:\boldsymbol{\lambda}\geqslant\mathrm{0}\:\:\mathrm{then}\:\mathrm{prove}\:\mathrm{that}: \\ $$$$\frac{\mathrm{x}}{\mathrm{y}^{\mathrm{3}} +\lambda\mathrm{y}^{\mathrm{2}} }\:+\:\frac{\mathrm{y}}{\mathrm{z}^{\mathrm{3}} +\lambda\mathrm{z}^{\mathrm{2}} }\:+\:\frac{\mathrm{z}}{\mathrm{x}^{\mathrm{3}} +\lambda\mathrm{x}^{\mathrm{2}} }\:\geqslant\:\frac{\mathrm{3}}{\lambda+\mathrm{1}} \\ $$

Question Number 161429 Answers: 0 Comments: 1

help me ! { ((x+3y+z=2)),((−3x+4y+2z=3)),((−2x+7y+3z=5)) :} Gauss Method...

$$\mathrm{help}\:\mathrm{me}\:! \\ $$$$\begin{cases}{{x}+\mathrm{3}{y}+{z}=\mathrm{2}}\\{−\mathrm{3}{x}+\mathrm{4}{y}+\mathrm{2}{z}=\mathrm{3}}\\{−\mathrm{2}{x}+\mathrm{7}{y}+\mathrm{3}{z}=\mathrm{5}}\end{cases} \\ $$$$\boldsymbol{\mathrm{G}}\mathrm{auss}\:\mathrm{Method}... \\ $$

Question Number 161424 Answers: 1 Comments: 0

Question Number 161418 Answers: 0 Comments: 0

4^(2021 ) =a^3 +b^3 +c^3 , (a:b:c)⇒ natural numbers

$$\mathrm{4}^{\mathrm{2021}\:} ={a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} ,\:\left({a}:{b}:{c}\right)\Rightarrow\:{natural}\:{numbers} \\ $$

Question Number 161416 Answers: 0 Comments: 0

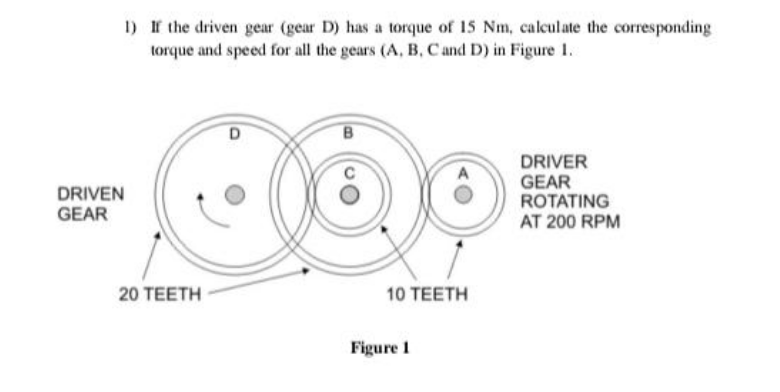
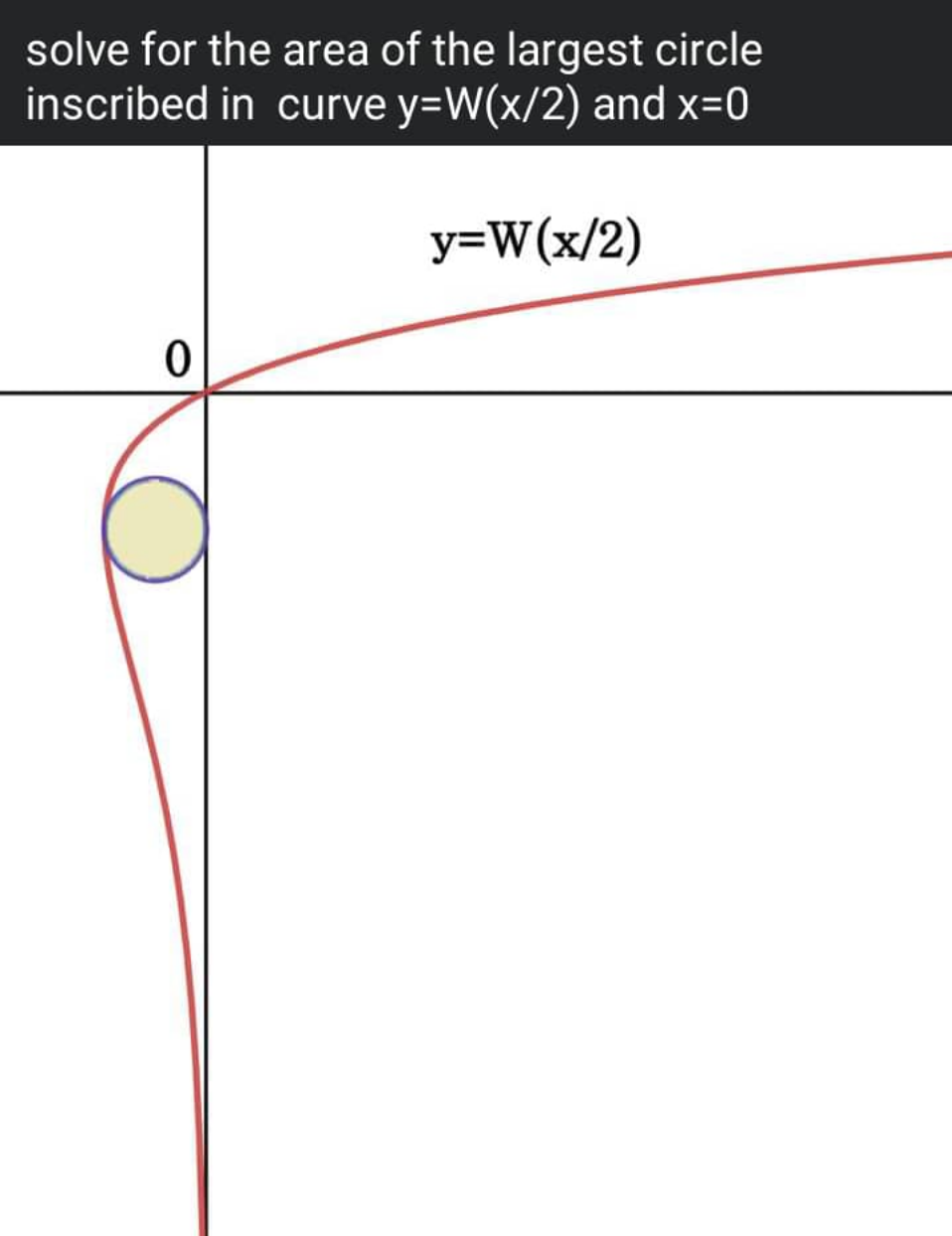
Question Number 161412 Answers: 0 Comments: 0

Question Number 161410 Answers: 0 Comments: 3

Question Number 161409 Answers: 2 Comments: 1

Calculate lim_(x→0) ((1−cos (1−cos x))/x^4 ) lim_(x→0) ((1−cos xcos 2xcos 3x)/x^2 )

$${Calculate} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:\left(\mathrm{1}−\mathrm{cos}\:{x}\right)}{{x}^{\mathrm{4}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:{x}\mathrm{cos}\:\mathrm{2}{x}\mathrm{cos}\:\mathrm{3}{x}}{{x}^{\mathrm{2}} } \\ $$

Question Number 161408 Answers: 1 Comments: 1

Question Number 161407 Answers: 1 Comments: 0

Question Number 161406 Answers: 0 Comments: 0

f (x ) = cos^( 2) ( x ) + sin^( 4) ( x ) R_( f) = ? −−−solution−−− y = cos^( 2) (x ) + sin^( 2) (x) .( 1−cos^( 2) (x)) = 1 − (1/4) sin^( 2) ( 2x) we know that : 0≤ sin^( 2) ( αx) ≤1 therefore −1≤− sin^( 2) (2x) ≤ 0 1−(1/4) ≤ 1− (1/4) sin^( 2) (2x) ≤1 R_( f) = [ (3/4) , 1 ] ◂ ★ ▶

Question Number 161404 Answers: 1 Comments: 0

Question Number 161403 Answers: 0 Comments: 0

Two force f1 act on a particle f1 has aa mgnitude of 5n in the direction 30 andf 2 has a magnitude of 8n in then directio of 90 fine the magnitude andi drection of their resultant

$$\mathrm{Two}\:\mathrm{force}\:\mathrm{f1}\:\mathrm{act}\:\mathrm{on}\:\mathrm{a}\:\mathrm{particle}\:\mathrm{f1}\:\mathrm{has}\:\mathrm{aa} \\ $$$$\mathrm{mgnitude}\:\mathrm{of}\:\mathrm{5n}\:\mathrm{in}\:\mathrm{the}\:\mathrm{direction}\:\mathrm{30}\:\mathrm{andf} \\ $$$$\mathrm{2}\:\mathrm{has}\:\mathrm{a}\:\mathrm{magnitude}\:\mathrm{of}\:\mathrm{8n}\:\mathrm{in}\:\mathrm{then} \\ $$$$\mathrm{directio}\:\mathrm{of}\:\mathrm{90}\:\mathrm{fine}\:\mathrm{the}\:\mathrm{magnitude}\:\mathrm{andi} \\ $$$$\mathrm{drection}\:\mathrm{of}\:\mathrm{their}\:\mathrm{resultant} \\ $$

Question Number 161396 Answers: 0 Comments: 2

If y = cos^2 x + sin^4 x for all values of x, then prove that (3/4) ≤ y ≤ 1

$$\mathrm{If}\:{y}\:=\:{cos}^{\mathrm{2}} {x}\:+\:{sin}^{\mathrm{4}} {x}\:\mathrm{for}\:\mathrm{all}\:\mathrm{values}\:\mathrm{of}\:\mathrm{x}, \\ $$$$\mathrm{then}\:\mathrm{prove}\:\mathrm{that}\: \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}\:\leq\:{y}\:\leq\:\mathrm{1} \\ $$

Question Number 161393 Answers: 0 Comments: 0

Question Number 161391 Answers: 0 Comments: 4

f^( 3) (x)+x^2 f(x)=2x^3 +4x^2 +3x+1 ∀x∈R

$$\:\:{f}^{\:\mathrm{3}} \left({x}\right)+{x}^{\mathrm{2}} \:{f}\left({x}\right)=\mathrm{2}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1} \\ $$$$\:\forall{x}\in\mathbb{R}\: \\ $$

Question Number 161387 Answers: 0 Comments: 0

sin(√(1+π^2 n^2 )) ∼ (((−1)^n )/(2πn)) ?

$$\:{sin}\sqrt{\mathrm{1}+\pi^{\mathrm{2}} {n}^{\mathrm{2}} }\:\sim\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}\pi{n}}\:\:? \\ $$

Question Number 161386 Answers: 0 Comments: 0

Question Number 161378 Answers: 0 Comments: 0

determine, pour tout α∈R, la nature de la serie de terme general U_n =Σ_(k=1) ^n (1/((k^2 +(n−k)^2 )^α )) besoin d′aide svp please help me

$${determine},\:{pour}\:{tout}\:\alpha\in\mathbb{R},\:\:{la}\:{nature} \\ $$$$\:{de}\:{la}\:{serie}\:{de}\:{terme}\:{general} \\ $$$${U}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\left({k}^{\mathrm{2}} +\left({n}−{k}\right)^{\mathrm{2}} \right)^{\alpha} } \\ $$$${besoin}\:{d}'{aide}\:{svp} \\ $$$${please}\:{help}\:{me} \\ $$

Question Number 161377 Answers: 3 Comments: 2

please calculate A and B. A = (1 − (1/4))(1 − (1/9))(1 − (1/(16)))...(1 − (1/(4 084 441))) (and 2021^(2 ) = 4084441 ) B = (1^2 −2^2 −3^2 + 4^2 ) + ( 5^2 − 6^2 −7^2 +8^2 ) +(9^2 −10^2 −11^2 +12^2 )+... +(2021^2 −2022^2 −2023^2 +2024^(2 ) )

$${please}\:{calculate}\:{A}\:{and}\:\:{B}. \\ $$$$ \\ $$$${A}\:=\:\left(\mathrm{1}\:−\:\frac{\mathrm{1}}{\mathrm{4}}\right)\left(\mathrm{1}\:−\:\frac{\mathrm{1}}{\mathrm{9}}\right)\left(\mathrm{1}\:−\:\frac{\mathrm{1}}{\mathrm{16}}\right)...\left(\mathrm{1}\:−\:\frac{\mathrm{1}}{\mathrm{4}\:\mathrm{084}\:\mathrm{441}}\right)\:\:\left({and}\:\mathrm{2021}^{\mathrm{2}\:} =\:\mathrm{4084441}\:\right) \\ $$$${B}\:=\:\left(\mathrm{1}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} \:−\mathrm{3}^{\mathrm{2}} \:+\:\mathrm{4}^{\mathrm{2}} \right)\:+\:\left(\:\mathrm{5}^{\mathrm{2}} \:−\:\mathrm{6}^{\mathrm{2}} \:−\mathrm{7}^{\mathrm{2}} \:+\mathrm{8}^{\mathrm{2}} \right)\:+\left(\mathrm{9}^{\mathrm{2}} \:−\mathrm{10}^{\mathrm{2}} \:−\mathrm{11}^{\mathrm{2}} \:+\mathrm{12}^{\mathrm{2}} \right)+...\:+\left(\mathrm{2021}^{\mathrm{2}} \:−\mathrm{2022}^{\mathrm{2}} \:−\mathrm{2023}^{\mathrm{2}} \:+\mathrm{2024}^{\mathrm{2}\:} \right) \\ $$

Pg 572 Pg 573 Pg 574 Pg 575 Pg 576 Pg 577 Pg 578 Pg 579 Pg 580 Pg 581

Contact: info@tinkutara.com