
AllQuestion and Answers: Page 570
Question Number 163134 Answers: 1 Comments: 0
Question Number 163126 Answers: 0 Comments: 1
Question Number 163125 Answers: 0 Comments: 0

Question Number 163120 Answers: 1 Comments: 0
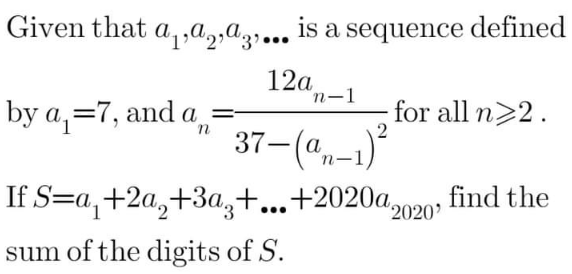
Question Number 163119 Answers: 2 Comments: 0
Question Number 163114 Answers: 1 Comments: 0
Question Number 163113 Answers: 0 Comments: 0
Question Number 163111 Answers: 2 Comments: 0
Question Number 163098 Answers: 2 Comments: 0

Question Number 163095 Answers: 0 Comments: 2
$${what}\:{the}\:{best}\:{math}'{s}\:{app}\:{for}\:{android}\:{and}\:{pc}? \\ $$
Question Number 163082 Answers: 0 Comments: 3
Question Number 163109 Answers: 1 Comments: 0
Question Number 163080 Answers: 1 Comments: 0
Question Number 163099 Answers: 1 Comments: 0
Question Number 163101 Answers: 0 Comments: 0

Question Number 163100 Answers: 1 Comments: 0
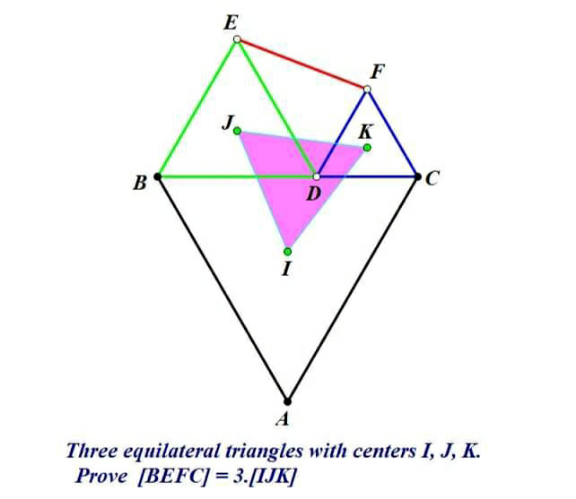
Question Number 163075 Answers: 2 Comments: 0
Question Number 163061 Answers: 1 Comments: 0
Question Number 163060 Answers: 1 Comments: 1
Question Number 163053 Answers: 1 Comments: 1

Question Number 163048 Answers: 3 Comments: 0

Question Number 163045 Answers: 1 Comments: 0
Question Number 163043 Answers: 0 Comments: 0
Question Number 163042 Answers: 0 Comments: 0
Question Number 163041 Answers: 0 Comments: 0
Question Number 163040 Answers: 0 Comments: 0
Pg 565 Pg 566 Pg 567 Pg 568 Pg 569 Pg 570 Pg 571 Pg 572 Pg 573 Pg 574
