Question and Answers Forum

AllQuestion and Answers: Page 569

Question Number 161586 Answers: 2 Comments: 2

lim_(x→2^− ) ((2−2cos (√(x−2)))/((x−2)^2 )) =?

$$\:\:\underset{{x}\rightarrow\mathrm{2}^{−} } {\mathrm{lim}}\:\frac{\mathrm{2}−\mathrm{2cos}\:\sqrt{{x}−\mathrm{2}}}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} }\:=? \\ $$

Question Number 161583 Answers: 3 Comments: 1

lim_(x→2) ((1−sin (π/x))/(x^2 −4x+4)) =? lim_(x→2) ((x^3 −8+sin πx)/(2−x))=? lim_(x→1) ((x^2 −1)/(cos ((π/(x+1)))))=?

$$\:\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{sin}\:\frac{\pi}{{x}}}{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}}\:=? \\ $$$$\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{3}} −\mathrm{8}+\mathrm{sin}\:\pi{x}}{\mathrm{2}−{x}}=? \\ $$$$\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{cos}\:\left(\frac{\pi}{{x}+\mathrm{1}}\right)}=? \\ $$

Question Number 161578 Answers: 1 Comments: 1

Question Number 161579 Answers: 1 Comments: 1

A gardener wishes to make a rectangular hen run of area 128m² against a wall which is to serve as one of the boundaries. Find the length of the wire netting required for the other three sides

$$ \\ $$A gardener wishes to make a rectangular hen run of area 128m² against a wall which is to serve as one of the boundaries. Find the length of the wire netting required for the other three sides

Question Number 161575 Answers: 1 Comments: 0

∫_0 ^9 ((√x)/(1−x))dx=?

$$\int_{\mathrm{0}} ^{\mathrm{9}} \frac{\sqrt{{x}}}{\mathrm{1}−{x}}{dx}=? \\ $$$$ \\ $$

Question Number 161764 Answers: 2 Comments: 5

Question Number 161567 Answers: 2 Comments: 0

let f(x) be f(x) = (x/(ln(1 - x))) prove there exists a sequence {a_k } such that D[f(x)] = [Σ_0 ^( ∞) a_k x^k ] [f(x)]^2

$$\mathrm{let}\:\:\mathrm{f}\left(\mathrm{x}\right)\:\:\mathrm{be} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{x}}{\mathrm{ln}\left(\mathrm{1}\:-\:\mathrm{x}\right)} \\ $$$$\mathrm{prove}\:\mathrm{there}\:\mathrm{exists}\:\mathrm{a}\:\mathrm{sequence}\:\left\{\mathrm{a}_{\boldsymbol{\mathrm{k}}} \right\}\:\mathrm{such}\:\mathrm{that} \\ $$$$\mathrm{D}\left[\mathrm{f}\left(\mathrm{x}\right)\right]\:=\:\left[\underset{\mathrm{0}} {\overset{\:\infty} {\sum}}\:\mathrm{a}_{\boldsymbol{\mathrm{k}}} \:\mathrm{x}^{\boldsymbol{\mathrm{k}}} \right]\:\left[\mathrm{f}\left(\mathrm{x}\right)\right]^{\mathrm{2}} \\ $$

Question Number 161566 Answers: 0 Comments: 0

if x;y;z>0 then prove that: Σ (x/( ((y^3 + 25xyz + z^3 ))^(1/3) )) ≥ 1

$$\mathrm{if}\:\:\mathrm{x};\mathrm{y};\mathrm{z}>\mathrm{0}\:\:\mathrm{then}\:\mathrm{prove}\:\mathrm{that}: \\ $$$$\Sigma\:\frac{\mathrm{x}}{\:\sqrt[{\mathrm{3}}]{\mathrm{y}^{\mathrm{3}} \:+\:\mathrm{25xyz}\:+\:\mathrm{z}^{\mathrm{3}} }}\:\geqslant\:\mathrm{1} \\ $$

Question Number 161564 Answers: 1 Comments: 1

Find all values x;y;z>0 such that: { ((x + y + 2z = 6)),(((3/y)∙((2/x) + (1/y)) = 4∙((2/(x + y)) + (1/(2y)))^2 )),((x + 2^y + log_2 z = 4)) :}

$$\mathrm{Find}\:\mathrm{all}\:\mathrm{values}\:\:\mathrm{x};\mathrm{y};\mathrm{z}>\mathrm{0}\:\:\mathrm{such}\:\mathrm{that}: \\ $$$$\begin{cases}{\mathrm{x}\:+\:\mathrm{y}\:+\:\mathrm{2z}\:=\:\mathrm{6}}\\{\frac{\mathrm{3}}{\mathrm{y}}\centerdot\left(\frac{\mathrm{2}}{\mathrm{x}}\:+\:\frac{\mathrm{1}}{\mathrm{y}}\right)\:=\:\mathrm{4}\centerdot\left(\frac{\mathrm{2}}{\mathrm{x}\:+\:\mathrm{y}}\:+\:\frac{\mathrm{1}}{\mathrm{2y}}\right)^{\mathrm{2}} }\\{\mathrm{x}\:+\:\mathrm{2}^{\boldsymbol{\mathrm{y}}} \:+\:\mathrm{log}_{\mathrm{2}} \boldsymbol{\mathrm{z}}\:=\:\mathrm{4}}\end{cases} \\ $$

Question Number 161563 Answers: 1 Comments: 0

Solve the equation: x+(√(x+(√(x+(√(x+ ...)))))) = x∙(√(x∙(√(x∙(√(x∙ ...)))))) where , x>0

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}: \\ $$$$\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\:...}}}\:=\:\mathrm{x}\centerdot\sqrt{\mathrm{x}\centerdot\sqrt{\mathrm{x}\centerdot\sqrt{\mathrm{x}\centerdot\:...}}} \\ $$$$\mathrm{where}\:,\:\mathrm{x}>\mathrm{0} \\ $$

Question Number 161560 Answers: 1 Comments: 0

lim_(x→+∞) 1+x^2 −2x^2 ln(x)=...?

$${li}\underset{{x}\rightarrow+\infty} {{m}}\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{2}{x}^{\mathrm{2}} {ln}\left({x}\right)=...? \\ $$

Question Number 161559 Answers: 1 Comments: 0

please show that (1/2) + cosx + cos2x + cos3x + ... + cosnx = ((sin[(n+1)(x/2)])/(2sin(x/2)))

$${please}\:{show}\:{that} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:+\:{cosx}\:+\:{cos}\mathrm{2}{x}\:+\:{cos}\mathrm{3}{x}\:+\:...\:+\:{cosnx}\:=\:\frac{{sin}\left[\left({n}+\mathrm{1}\right)\frac{{x}}{\mathrm{2}}\right]}{\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}} \\ $$

Question Number 161558 Answers: 1 Comments: 0

What′s the value of a for which x^2 +x=a & x^2 −3x+2=a have one root common?

$${What}'{s}\:{the}\:{value}\:{of}\:{a}\:{for}\:{which} \\ $$$${x}^{\mathrm{2}} +{x}={a}\:\&\:{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}={a}\:{have}\:{one} \\ $$$${root}\:{common}? \\ $$

Question Number 161553 Answers: 0 Comments: 0

lim_(t→+∞) tΣ_(k=0) ^∞ (((−1)^k )/( (√(k^2 +t^2 ))))=?

$$\underset{\mathrm{t}\rightarrow+\infty} {\mathrm{lim}t}\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\:\sqrt{\mathrm{k}^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} }}=? \\ $$

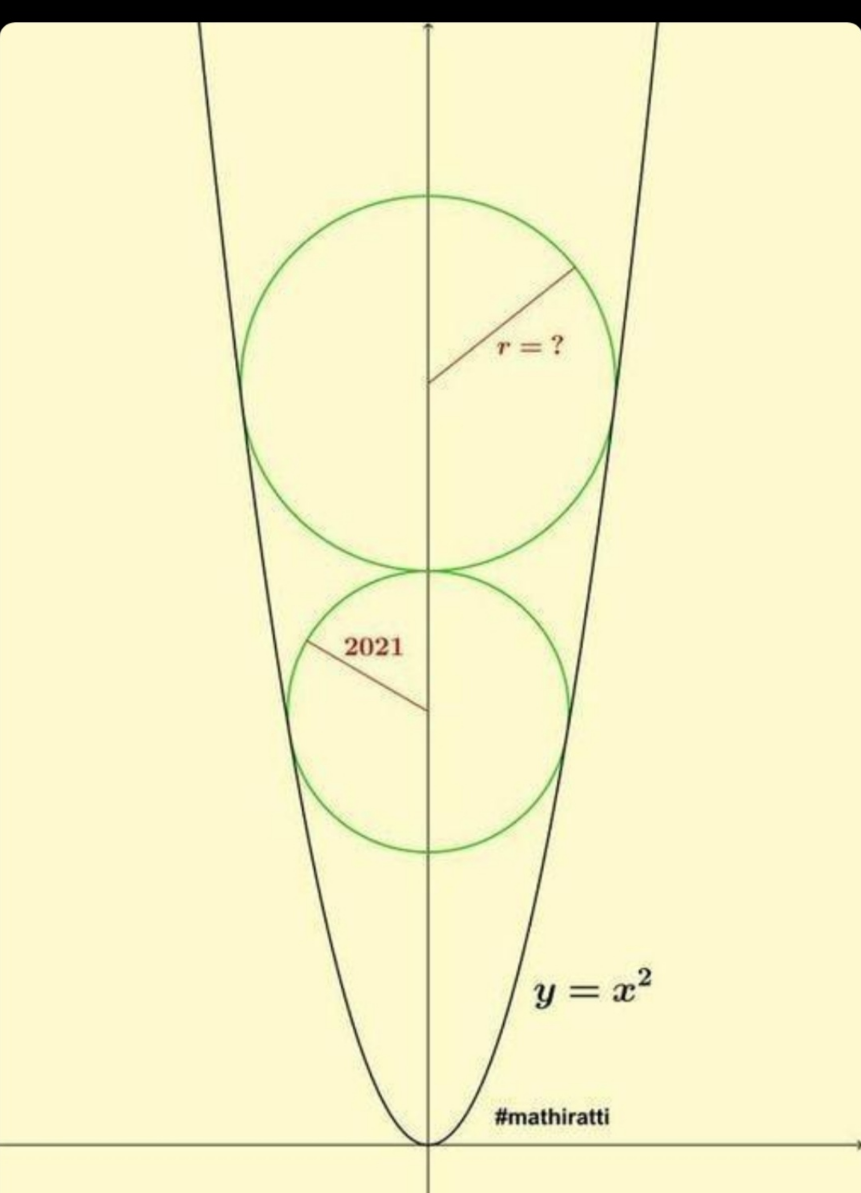
Question Number 161537 Answers: 2 Comments: 0

∫_0 ^( (π/4)) ((1+tan^4 (x))/(cot^2 (x))) dx =?

$$\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{1}+\mathrm{tan}\:^{\mathrm{4}} \left({x}\right)}{\mathrm{cot}\:^{\mathrm{2}} \left({x}\right)}\:{dx}\:=? \\ $$

Question Number 161533 Answers: 1 Comments: 1

Question Number 161529 Answers: 0 Comments: 0

lim_(n→∞) n((∫_1 ^(+∞) ((x^n −x^2 +1)/(x^2 (x^n +1)))dx)^n −(1/2))=?

$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}n}\left(\left(\int_{\mathrm{1}} ^{+\infty} \frac{\mathrm{x}^{\mathrm{n}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{n}} +\mathrm{1}\right)}\mathrm{dx}\right)^{\mathrm{n}} −\frac{\mathrm{1}}{\mathrm{2}}\right)=? \\ $$

Question Number 161528 Answers: 1 Comments: 0

PROVE that the numbers of types 4k+2 & 4k+3 are NOT perfect □s.

$$\mathrm{PROVE}\:\mathrm{that}\:\mathrm{the}\:\mathrm{numbers}\:\mathrm{of}\:\mathrm{types} \\ $$$$\mathrm{4k}+\mathrm{2}\:\&\:\mathrm{4k}+\mathrm{3}\:\mathrm{are}\:\mathrm{NOT}\:\mathrm{perfect}\:\Box\mathrm{s}. \\ $$

Question Number 161527 Answers: 0 Comments: 0

Question Number 161521 Answers: 0 Comments: 3

x^8 +ax^4 +1=0 a=? is x_1 +x_2 +x_3 +x_4 =?

$$\boldsymbol{\mathrm{x}}^{\mathrm{8}} +\boldsymbol{\mathrm{ax}}^{\mathrm{4}} +\mathrm{1}=\mathrm{0} \\ $$$$\boldsymbol{{a}}=?\: \\ $$$$\boldsymbol{{is}}\:\:\boldsymbol{{x}}_{\mathrm{1}} +\boldsymbol{{x}}_{\mathrm{2}} +\boldsymbol{{x}}_{\mathrm{3}} +\boldsymbol{{x}}_{\mathrm{4}} =? \\ $$

Question Number 161516 Answers: 0 Comments: 2

f′(a) is derivative of function f(a) . lim_(h→0) ((f(a−2h^2 )−f(a+h^3 ))/h^2 ) = ?

$${f}'\left({a}\right)\:\:{is}\:\:{derivative}\:\:{of}\:\:{function}\:\:{f}\left({a}\right)\:. \\ $$$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{{f}\left({a}−\mathrm{2}{h}^{\mathrm{2}} \right)−{f}\left({a}+{h}^{\mathrm{3}} \right)}{{h}^{\mathrm{2}} }\:\:=\:\:? \\ $$

Question Number 161513 Answers: 0 Comments: 0

find the value of −1−1/3^2 −1/5^2 −1/7^2 −...

$$\boldsymbol{{find}}\:\boldsymbol{{the}}\:\boldsymbol{{value}}\:\boldsymbol{{of}} \\ $$$$−\mathrm{1}−\mathrm{1}/\mathrm{3}^{\mathrm{2}} −\mathrm{1}/\mathrm{5}^{\mathrm{2}} −\mathrm{1}/\mathrm{7}^{\mathrm{2}} −... \\ $$

Question Number 161507 Answers: 2 Comments: 0

Question Number 161505 Answers: 1 Comments: 3

((a + ((a+8)/3) (√((a−1)/3))))^(1/3) + ((a − ((a+8)/3) (√((a−1)/3))))^(1/3) = ?

$$\sqrt[{\mathrm{3}}]{{a}\:+\:\frac{{a}+\mathrm{8}}{\mathrm{3}}\:\sqrt{\frac{{a}−\mathrm{1}}{\mathrm{3}}}}\:+\:\sqrt[{\mathrm{3}}]{{a}\:−\:\frac{{a}+\mathrm{8}}{\mathrm{3}}\:\sqrt{\frac{{a}−\mathrm{1}}{\mathrm{3}}}}\:\:=\:\:? \\ $$

Question Number 161504 Answers: 1 Comments: 0

Montrer a^ partir du crite^ re de Cauchy que U_n =Σ_(k=1) ^n (1/k^2 ) est une de Cauchy. −−−−−−−−−−−−−−−− Show by using Cauchy′s sequence definition that U_n =Σ_(k=1) ^n (1/k^2 ) is a sequence of Cauchy.

$${Montrer}\:\grave {{a}}\:{partir}\:{du}\:{crit}\grave {{e}re}\:{de}\: \\ $$$${Cauchy}\:{que}\:{U}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:{est}\:{une} \\ $$$${de}\:{Cauchy}. \\ $$$$−−−−−−−−−−−−−−−− \\ $$$${Show}\:{by}\:{using}\:{Cauchy}'{s}\:{sequence} \\ $$$${definition}\:{that}\:{U}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:{is}\:{a}\: \\ $$$${sequence}\:{of}\:{Cauchy}. \\ $$

Question Number 161500 Answers: 1 Comments: 0

x^6 - 6x^5 + ax^4 + bx^3 + cx^2 + dx + 1 = 0 all the roots of the equation are positive find a+b+c+d=?

$$\mathrm{x}^{\mathrm{6}} \:-\:\mathrm{6x}^{\mathrm{5}} \:+\:\mathrm{ax}^{\mathrm{4}} \:+\:\mathrm{bx}^{\mathrm{3}} \:+\:\mathrm{cx}^{\mathrm{2}} \:+\:\mathrm{dx}\:+\:\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{all}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{are}\:\mathrm{positive} \\ $$$$\mathrm{find}\:\:\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}=? \\ $$

Pg 564 Pg 565 Pg 566 Pg 567 Pg 568 Pg 569 Pg 570 Pg 571 Pg 572 Pg 573

Contact: info@tinkutara.com