Question and Answers Forum

AllQuestion and Answers: Page 567

Question Number 161931 Answers: 0 Comments: 4

If (( 1−sin(x)−cos(x))/(1+sin(x)−cos(x))) = (1/4) then find the value of: tan(x) + (1/(cos(x))) =?

$$ \\ $$$$\:\:\:\:\:\:\mathrm{I}{f}\:\:\:\:\frac{\:\mathrm{1}−{sin}\left({x}\right)−{cos}\left({x}\right)}{\mathrm{1}+{sin}\left({x}\right)−{cos}\left({x}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:{then}\:\:{find}\:{the}\:{value}\:{of}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{tan}\left({x}\right)\:+\:\frac{\mathrm{1}}{{cos}\left({x}\right)}\:=? \\ $$$$\:\:\:\:\:\: \\ $$$$ \\ $$

Question Number 161930 Answers: 1 Comments: 0

{ ((a_0 =−2 )),((a_n =a_(n−1) +2n)) :} ; a_n =?

$$\begin{cases}{{a}_{\mathrm{0}} =−\mathrm{2}\:}\\{{a}_{{n}} ={a}_{{n}−\mathrm{1}} +\mathrm{2}{n}}\end{cases}\:\:\:\:\:;\:{a}_{{n}} =? \\ $$

Question Number 161926 Answers: 0 Comments: 0

Question Number 161919 Answers: 1 Comments: 0

∫_(−∞) ^( ∞) sin(x^2 +x+1)dx

$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\int_{−\infty} ^{\:\infty} \:\mathrm{sin}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right){dx}\: \\ $$$$\: \\ $$

Question Number 161917 Answers: 0 Comments: 0

∫_(−∞) ^( ∞) (1/( (√(x^4 +x+1)) )) dx

$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{−\infty} ^{\:\infty} \:\frac{\mathrm{1}}{\:\sqrt{{x}^{\mathrm{4}} +{x}+\mathrm{1}}\:}\:{dx} \\ $$$$\: \\ $$

Question Number 161914 Answers: 1 Comments: 0

If , x^( 2) + 9y^( 2) + 4x +18y −23=0 then find the value of , M_ ax ( 3x+2y ) . −−−−−−−−−

$$\:\mathrm{If}\:, \\ $$$$\:\:\:{x}^{\:\mathrm{2}} \:+\:\mathrm{9}{y}^{\:\mathrm{2}} \:+\:\mathrm{4}{x}\:+\mathrm{18}{y}\:−\mathrm{23}=\mathrm{0} \\ $$$$ \\ $$$$\:{then}\:\:{find}\:{the}\:{value}\:\:{of}\:\:,\:\:\mathrm{M}_{\:} {ax}\:\left(\:\mathrm{3}{x}+\mathrm{2}{y}\:\right)\:. \\ $$$$\:−−−−−−−−− \\ $$$$ \\ $$

Question Number 161912 Answers: 1 Comments: 6

Question Number 162027 Answers: 1 Comments: 0

Question Number 161907 Answers: 0 Comments: 1

(1)((1/2)+cos (π/(20)))((1/2)+cos ((3π)/(20)))((1/2)+cos ((9π)/(20)))((1/2)+cos ((27π)/(20)))=? (2) tan (π/(30)) tan ((7π)/(30)) tan ((11π)/(30)) =?

$$\left(\mathrm{1}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:\frac{\pi}{\mathrm{20}}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{20}}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:\frac{\mathrm{9}\pi}{\mathrm{20}}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{cos}\:\frac{\mathrm{27}\pi}{\mathrm{20}}\right)=? \\ $$$$\left(\mathrm{2}\right)\:\mathrm{tan}\:\frac{\pi}{\mathrm{30}}\:\mathrm{tan}\:\frac{\mathrm{7}\pi}{\mathrm{30}}\:\mathrm{tan}\:\frac{\mathrm{11}\pi}{\mathrm{30}}\:=? \\ $$

Question Number 161903 Answers: 2 Comments: 1

((1−sin(x)−cos(x))/(1+sin(x)−cos(x)))=???

$$\frac{\mathrm{1}−\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)−\boldsymbol{{cos}}\left(\boldsymbol{{x}}\right)}{\mathrm{1}+\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)−\boldsymbol{{cos}}\left(\boldsymbol{{x}}\right)}=??? \\ $$$$ \\ $$

Question Number 161900 Answers: 1 Comments: 0

0<x;y;z<1 (1-x)(1-y)(1-z)=xyz Find: Ω = min (((1-x)/(xy)) + ((1-y)/(yz)) + ((1-z)/(zx)))

$$\mathrm{0}<\mathrm{x};\mathrm{y};\mathrm{z}<\mathrm{1} \\ $$$$\left(\mathrm{1}-\mathrm{x}\right)\left(\mathrm{1}-\mathrm{y}\right)\left(\mathrm{1}-\mathrm{z}\right)=\mathrm{xyz} \\ $$$$\mathrm{Find}: \\ $$$$\Omega\:=\:\mathrm{min}\:\left(\frac{\mathrm{1}-\mathrm{x}}{\mathrm{xy}}\:+\:\frac{\mathrm{1}-\mathrm{y}}{\mathrm{yz}}\:+\:\frac{\mathrm{1}-\mathrm{z}}{\mathrm{zx}}\right) \\ $$

Question Number 161899 Answers: 2 Comments: 0

Find: 𝛀 =∫_( -∞) ^( ∞) (1/((1 + x^(2n) )^2 )) dx ; n∈Z

$$\mathrm{Find}: \\ $$$$\boldsymbol{\Omega}\:=\underset{\:-\infty} {\overset{\:\infty} {\int}}\frac{\mathrm{1}}{\left(\mathrm{1}\:+\:\mathrm{x}^{\mathrm{2}\boldsymbol{\mathrm{n}}} \right)^{\mathrm{2}} }\:\mathrm{dx}\:\:;\:\:\mathrm{n}\in\mathbb{Z} \\ $$

Question Number 161884 Answers: 0 Comments: 2

Solve for real numbers: ((2^x + 2^(-1) ))^(1/7) = 1 + ((2^x - 2^(-1) ))^(1/7)

$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{real}\:\mathrm{numbers}: \\ $$$$\sqrt[{\mathrm{7}}]{\mathrm{2}^{\boldsymbol{\mathrm{x}}} \:+\:\mathrm{2}^{-\mathrm{1}} }\:=\:\mathrm{1}\:+\:\sqrt[{\mathrm{7}}]{\mathrm{2}^{\boldsymbol{\mathrm{x}}} \:-\:\mathrm{2}^{-\mathrm{1}} } \\ $$

Question Number 162231 Answers: 1 Comments: 0

nature et calcul ∫_0 ^1 ((lnx)/( (√(1−x))))dx

$${nature}\:{et}\:{calcul} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{lnx}}{\:\sqrt{\mathrm{1}−{x}}}{dx} \\ $$

Question Number 161875 Answers: 0 Comments: 0

Question Number 161888 Answers: 1 Comments: 5

help me ! solve this one : C_(40) ^(2n) = C_(40) ^(16+n)

$$\mathrm{help}\:\mathrm{me}\:! \\ $$$$\mathrm{solve}\:\mathrm{this}\:\mathrm{one}\::\:\mathrm{C}_{\mathrm{40}} ^{\mathrm{2n}} \:=\:\mathrm{C}_{\mathrm{40}} ^{\mathrm{16}+\mathrm{n}} \\ $$

Question Number 161868 Answers: 1 Comments: 0

((√(2+(√3))) )^x + (1/(((√(2+(√3))))^x )) = 2^x x=?

$$\:\:\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\:\right)^{{x}} \:+\:\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\right)^{{x}} }\:=\:\mathrm{2}^{{x}} \\ $$$$\:\:{x}=? \\ $$

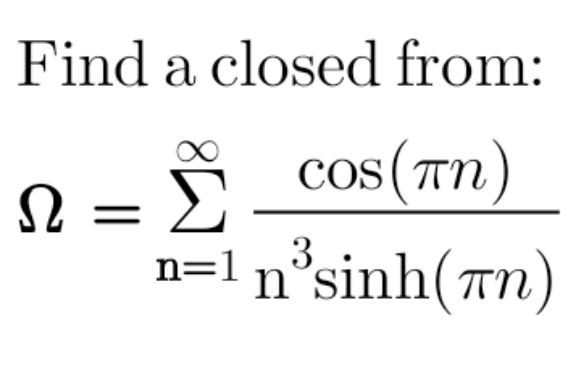
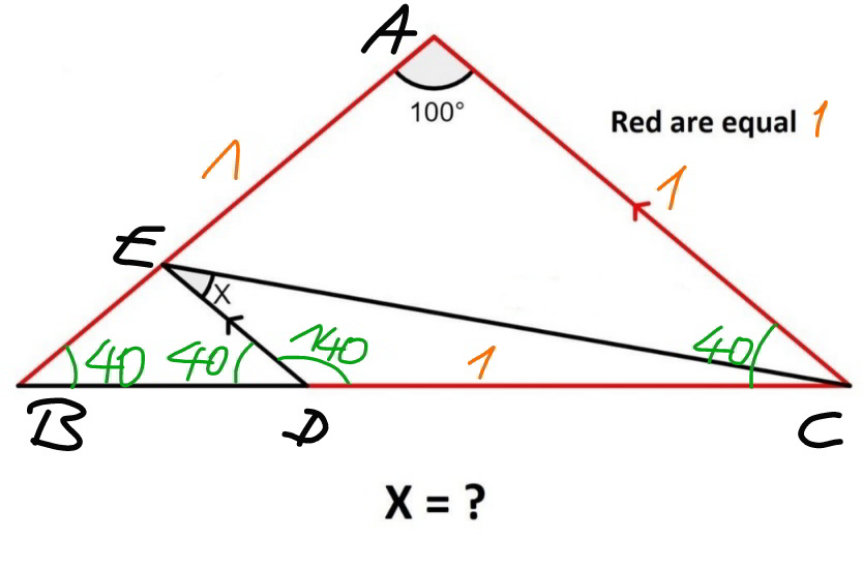
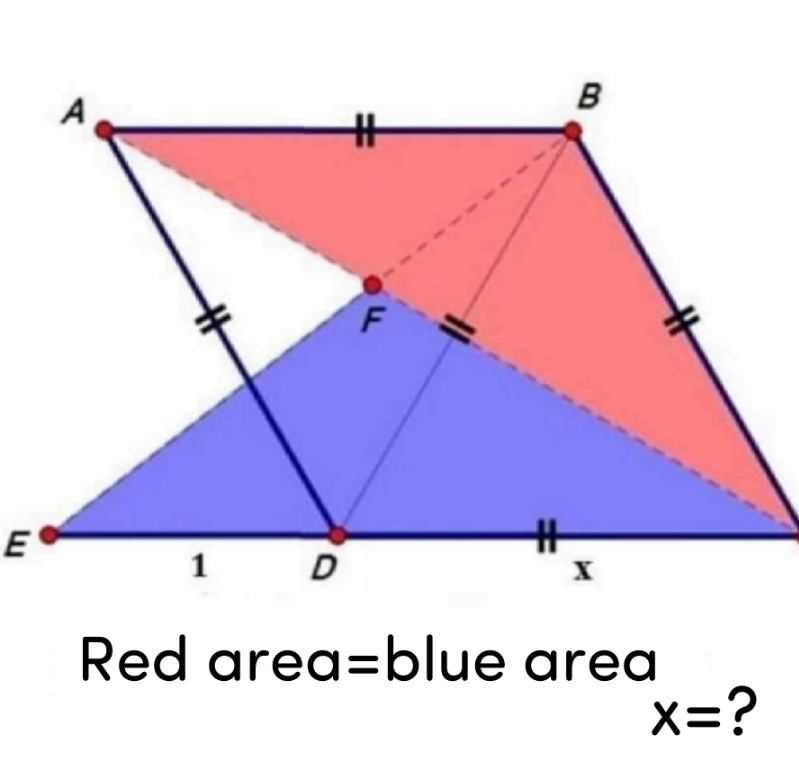
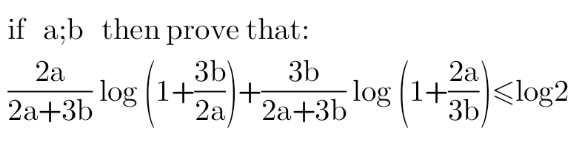
Question Number 161867 Answers: 1 Comments: 0

lim_(x→∞) ((√(x^2 +8x+9)) −(√(x^2 +5x+4)) )^(4x) = ?

$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{9}}\:−\sqrt{{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{4}}\:\right)^{\mathrm{4}{x}} \:=\:? \\ $$

Question Number 161866 Answers: 1 Comments: 3

Question Number 161862 Answers: 0 Comments: 0

Question Number 161861 Answers: 1 Comments: 8

Prove that ((1^2 ∙2!+2^2 ∙3!+3^2 ∙4!+∙∙∙+n^2 (n+1)!−2)/((n+1)!)) =n^2 +n−2

$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\:\:\:\frac{\mathrm{1}^{\mathrm{2}} \centerdot\mathrm{2}!+\mathrm{2}^{\mathrm{2}} \centerdot\mathrm{3}!+\mathrm{3}^{\mathrm{2}} \centerdot\mathrm{4}!+\centerdot\centerdot\centerdot+{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)!−\mathrm{2}}{\left({n}+\mathrm{1}\right)!} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={n}^{\mathrm{2}} +{n}−\mathrm{2} \\ $$

Question Number 161860 Answers: 1 Comments: 0

Simplify ((1^2 ∙2!+2^2 ∙3!+3^2 ∙4!+∙∙∙+n^2 (n+1)!−2)/((n+1)!)) to n^2 +n−2

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{Simplify} \\ $$$$\frac{\mathrm{1}^{\mathrm{2}} \centerdot\mathrm{2}!+\mathrm{2}^{\mathrm{2}} \centerdot\mathrm{3}!+\mathrm{3}^{\mathrm{2}} \centerdot\mathrm{4}!+\centerdot\centerdot\centerdot+{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)!−\mathrm{2}}{\left({n}+\mathrm{1}\right)!} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{to} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{n}^{\mathrm{2}} +\mathrm{n}−\mathrm{2} \\ $$

Question Number 161854 Answers: 1 Comments: 1

Question Number 161848 Answers: 0 Comments: 2

If tan (α )= 2 find the value of K=(( 1+sin( 8 α)−cos (8α ))/(1+sin( 8α ) + cos (8 α ))) =?

$$ \\ $$$$\:\:\:\:\:\:\mathrm{I}{f}\:\:\:\:{tan}\:\left(\alpha\:\right)=\:\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:{find}\:{the}\:{value}\:{of}\: \\ $$$$\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\mathrm{K}=\frac{\:\:\mathrm{1}+{sin}\left(\:\mathrm{8}\:\alpha\right)−{cos}\:\left(\mathrm{8}\alpha\:\right)}{\mathrm{1}+{sin}\left(\:\mathrm{8}\alpha\:\right)\:+\:{cos}\:\left(\mathrm{8}\:\alpha\:\right)}\:=? \\ $$$$ \\ $$$$ \\ $$

Question Number 161843 Answers: 0 Comments: 3

Q#161744 reposted with some change. Solve for integer numbers: (x/y) + (5/x) + ((y - 5)/5) = ((y + x)/(y + 5)) + ((5 + y)/(5 + x))

$${Q}#\mathrm{161744}\:{reposted}\:{with}\:{some}\:{change}. \\ $$$$\mathrm{Solve}\:\mathrm{for}\:\boldsymbol{\mathrm{integer}}\:\mathrm{numbers}: \\ $$$$\frac{\mathrm{x}}{\mathrm{y}}\:+\:\frac{\mathrm{5}}{\mathrm{x}}\:+\:\frac{\mathrm{y}\:-\:\mathrm{5}}{\mathrm{5}}\:=\:\frac{\mathrm{y}\:+\:\mathrm{x}}{\mathrm{y}\:+\:\mathrm{5}}\:+\:\frac{\mathrm{5}\:+\:\mathrm{y}}{\mathrm{5}\:+\:\mathrm{x}} \\ $$

Question Number 161839 Answers: 3 Comments: 0

calculate ∫_(−∞) ^(+∞) (dx/((x^2 +2x+2)^2 ))

$$\mathrm{calculate}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{2}\right)^{\mathrm{2}} } \\ $$

Pg 562 Pg 563 Pg 564 Pg 565 Pg 566 Pg 567 Pg 568 Pg 569 Pg 570 Pg 571

Contact: info@tinkutara.com