Question and Answers Forum

All Questions   Topic List

AllQuestion and Answers: Page 566

Question Number 163223    Answers: 1   Comments: 0

The arc of parabola y=−x^2 +9 in 0<x<3 is revolved about the line y=c and 0<c<9 to generate a solid. Find the value of c that minimizes the volume of the solid.

$$\mathrm{The}\:\mathrm{arc}\:\mathrm{of}\:\mathrm{parabola}\:{y}=−{x}^{\mathrm{2}} +\mathrm{9}\:\mathrm{in}\:\mathrm{0}<{x}<\mathrm{3} \\ $$$$\mathrm{is}\:\mathrm{revolved}\:\mathrm{about}\:\mathrm{the}\:\mathrm{line}\:{y}={c}\:\mathrm{and}\:\mathrm{0}<{c}<\mathrm{9} \\ $$$$\mathrm{to}\:\mathrm{generate}\:\mathrm{a}\:\mathrm{solid}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{c}\:\mathrm{that}\:\mathrm{minimizes}\:\mathrm{the}\: \\ $$$$\mathrm{volume}\:\mathrm{of}\:\mathrm{the}\:\mathrm{solid}. \\ $$

Question Number 163222    Answers: 1   Comments: 0

(√(((√(x+4)) +2)/(2−(√(x+4))))) ≤ x−4

$$\:\:\:\sqrt{\frac{\sqrt{{x}+\mathrm{4}}\:+\mathrm{2}}{\mathrm{2}−\sqrt{{x}+\mathrm{4}}}}\:\leqslant\:{x}−\mathrm{4}\: \\ $$

Question Number 163217    Answers: 0   Comments: 0

Question Number 163211    Answers: 0   Comments: 0

Question Number 163210    Answers: 1   Comments: 1

Question Number 163209    Answers: 0   Comments: 0

f : I → (0 ; ∞) ; I ⊂ R f - twice derivable ; f^′ ; f^(′′) - continuous f^(′′) (x) f(x) ≥ (f^′ (x))^2 ; ∀ x ∈ I then prove that: 2f (((x + y)/2)) ≤ f(x) + f(y) ; ∀ x;y ∈ I

$$\mathrm{f}\::\:\mathrm{I}\:\rightarrow\:\left(\mathrm{0}\:;\:\infty\right)\:\:;\:\:\mathrm{I}\:\subset\:\mathbb{R} \\ $$$$\mathrm{f}\:-\:\mathrm{twice}\:\mathrm{derivable}\:\:;\:\:\mathrm{f}\:^{'} \:;\:\mathrm{f}\:^{''} \:-\:\mathrm{continuous} \\ $$$$\mathrm{f}\:^{''} \left(\mathrm{x}\right)\:\mathrm{f}\left(\mathrm{x}\right)\:\geqslant\:\left(\mathrm{f}\:^{'} \left(\mathrm{x}\right)\right)^{\mathrm{2}} \:;\:\:\forall\:\mathrm{x}\:\in\:\mathrm{I} \\ $$$$\mathrm{then}\:\mathrm{prove}\:\mathrm{that}: \\ $$$$\mathrm{2f}\:\left(\frac{\mathrm{x}\:+\:\mathrm{y}}{\mathrm{2}}\right)\:\leqslant\:\mathrm{f}\left(\mathrm{x}\right)\:+\:\mathrm{f}\left(\mathrm{y}\right)\:\:;\:\:\forall\:\mathrm{x};\mathrm{y}\:\in\:\mathrm{I} \\ $$

Question Number 163205    Answers: 0   Comments: 0

Fourier series expansion for ln(sin(x))

$$\boldsymbol{{F}}{ourier}\:{series}\:{expansion}\:{for}\:{ln}\left({sin}\left({x}\right)\right) \\ $$

Question Number 163197    Answers: 0   Comments: 1

Question Number 163191    Answers: 0   Comments: 1

Question Number 163175    Answers: 0   Comments: 1

Question Number 163171    Answers: 1   Comments: 0

Prove that sin 36° = ((√(10−2(√5^ )))/4)

$$\mathrm{Prove}\:\mathrm{that}\:\:\:\mathrm{sin}\:\mathrm{36}°\:=\:\frac{\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}^{} }}}{\mathrm{4}} \\ $$

Question Number 163214    Answers: 0   Comments: 1

lim_(x→0) ((2sin x−2tan x+x^3 )/(6x−2sin 3x−9x^3 )) =?

$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2sin}\:{x}−\mathrm{2tan}\:{x}+{x}^{\mathrm{3}} }{\mathrm{6}{x}−\mathrm{2sin}\:\mathrm{3}{x}−\mathrm{9}{x}^{\mathrm{3}} }\:=? \\ $$

Question Number 163212    Answers: 1   Comments: 3

Question Number 163168    Answers: 2   Comments: 1

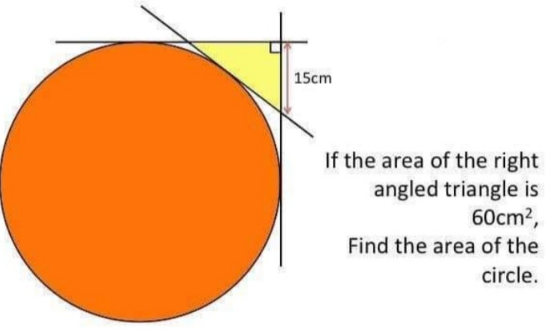
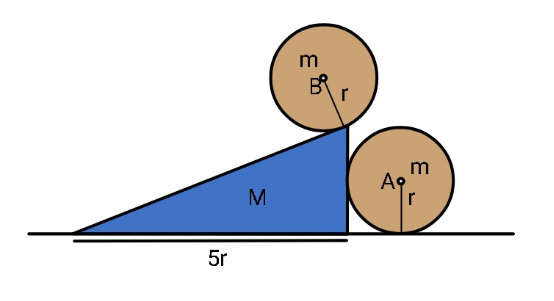
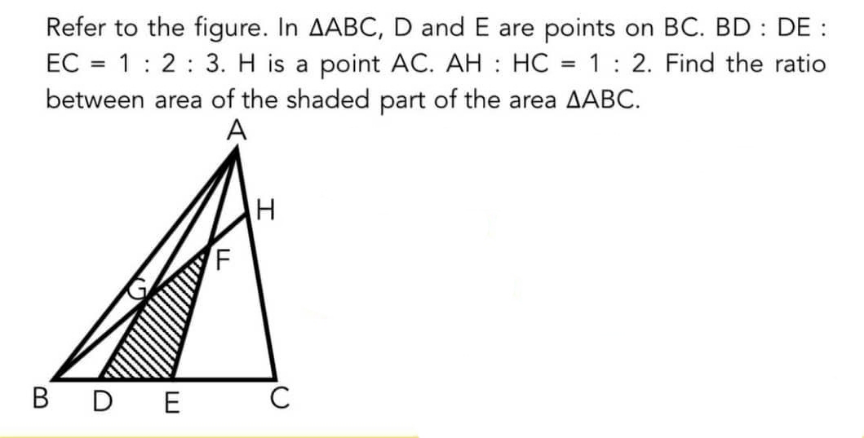
Question Number 163167    Answers: 1   Comments: 0

6^(x+1) +1 = 8^(x+1) −27^x x=?

$$\:\mathrm{6}^{{x}+\mathrm{1}} \:+\mathrm{1}\:=\:\mathrm{8}^{{x}+\mathrm{1}} −\mathrm{27}^{{x}} \: \\ $$$$\:{x}=? \\ $$

Question Number 163166    Answers: 0   Comments: 0

$$ \\ $$

Question Number 163163    Answers: 1   Comments: 1

x^9 −2022x^3 +(√(2021))=0 x={?}

$${x}^{\mathrm{9}} −\mathrm{2022}{x}^{\mathrm{3}} +\sqrt{\mathrm{2021}}=\mathrm{0} \\ $$$${x}=\left\{?\right\} \\ $$

Question Number 163161    Answers: 1   Comments: 0

Question Number 163158    Answers: 1   Comments: 0

prove that ∫_0 ^( (π/4)) (( sin(x)+cos(x))/( (√(1+sin(x)cos(x))))) dx= (√2) .cot^( −1) ((√2) ) −−−−−

$$ \\ $$$$\:\:\:\:\:{prove}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \frac{\:{sin}\left({x}\right)+{cos}\left({x}\right)}{\:\sqrt{\mathrm{1}+{sin}\left({x}\right){cos}\left({x}\right)}}\:{dx}=\:\sqrt{\mathrm{2}}\:.{cot}^{\:−\mathrm{1}} \left(\sqrt{\mathrm{2}}\:\right) \\ $$$$\:\:\:−−−−− \\ $$

Question Number 163153    Answers: 2   Comments: 0

show that ((cos(x−y))/(cos(x+y)))=((1+tanxtany)/(1−tanxtany))

$${show}\:{that} \\ $$$$\:\frac{{cos}\left({x}−{y}\right)}{{cos}\left({x}+{y}\right)}=\frac{\mathrm{1}+{tanxtany}}{\mathrm{1}−{tanxtany}} \\ $$

Question Number 163148    Answers: 1   Comments: 4

Question Number 163144    Answers: 1   Comments: 0

Find: 𝛀 = ∫_( 0) ^( 1) (((π/4) - arctan(x))/(1 - x)) dx

$$\mathrm{Find}:\:\:\:\boldsymbol{\Omega}\:=\:\underset{\:\mathrm{0}} {\overset{\:\mathrm{1}} {\int}}\:\frac{\frac{\pi}{\mathrm{4}}\:-\:\mathrm{arctan}\left(\mathrm{x}\right)}{\mathrm{1}\:-\:\mathrm{x}}\:\mathrm{dx} \\ $$

Question Number 163143    Answers: 0   Comments: 2

Question Number 163137    Answers: 1   Comments: 0

Soit U_n =((n−1)/(n^2 −5n+5)) avec n ∈ N. Montrer par la definition que U_n converge vers 0.

$${Soit}\:{U}_{{n}} =\frac{{n}−\mathrm{1}}{{n}^{\mathrm{2}} −\mathrm{5}{n}+\mathrm{5}}\:{avec}\:{n}\:\in\:\mathbb{N}. \\ $$$${Montrer}\:{par}\:{la}\:{definition}\:{que}\:{U}_{{n}} \: \\ $$$${converge}\:{vers}\:\mathrm{0}. \\ $$

Question Number 164451    Answers: 0   Comments: 1

How do you all to prove is true or false??; Prove the: (1/(1+p+p^2 +p^3 )) + (1/(1+q+q^2 +q^3 )) + (1/(1+r+r^2 +r^3 )) + (1/(1+s+s^2 +s^(3 ) )) ≥ 1

$$\boldsymbol{\mathrm{How}}\:\boldsymbol{\mathrm{do}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{all}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{true}}\:\boldsymbol{\mathrm{or}}\:\boldsymbol{\mathrm{false}}??; \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{Prove}}\:\boldsymbol{{the}}: \\ $$$$\:\frac{\mathrm{1}}{\mathrm{1}+\boldsymbol{\mathrm{p}}+\boldsymbol{\mathrm{p}}^{\mathrm{2}} +\boldsymbol{\mathrm{p}}^{\mathrm{3}} }\:+\:\frac{\mathrm{1}}{\mathrm{1}+\boldsymbol{{q}}+\boldsymbol{{q}}^{\mathrm{2}} +\boldsymbol{{q}}^{\mathrm{3}} }\:+\:\frac{\mathrm{1}}{\mathrm{1}+\boldsymbol{{r}}+\boldsymbol{{r}}^{\mathrm{2}} +\boldsymbol{{r}}^{\mathrm{3}} }\:+\:\frac{\mathrm{1}}{\mathrm{1}+\boldsymbol{{s}}+\boldsymbol{{s}}^{\mathrm{2}} +\boldsymbol{{s}}^{\mathrm{3}\:} }\:\geqslant\:\mathrm{1} \\ $$

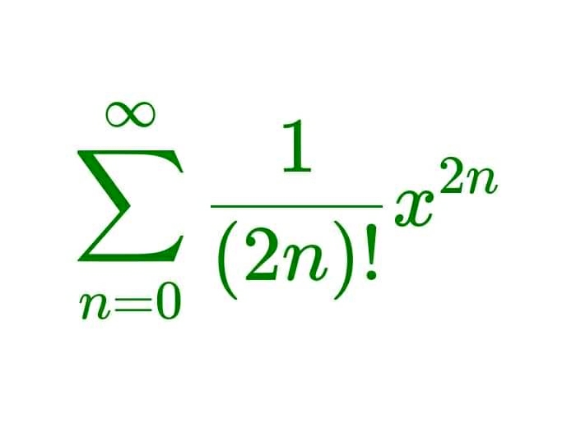
Question Number 163134    Answers: 1   Comments: 0

prove or disprove ∫_(2π) ^( 4π) (( sin(x))/x) dx >0 because ∫_(2π) ^( 3π) (( sin(x ))/x) dx > ∫_(3π) ^( 4π) ((∣sin(x)∣)/x) dx

$$ \\ $$$$\:\:\:\:{prove}\:\:{or}\:{disprove} \\ $$$$ \\ $$$$\:\:\:\:\int_{\mathrm{2}\pi} ^{\:\mathrm{4}\pi} \frac{\:{sin}\left({x}\right)}{{x}}\:{dx}\:>\mathrm{0} \\ $$$$\:\:\:\:\:\:\:{because} \\ $$$$\:\int_{\mathrm{2}\pi} ^{\:\mathrm{3}\pi} \frac{\:{sin}\left({x}\:\right)}{{x}}\:{dx}\:>\:\int_{\mathrm{3}\pi} ^{\:\mathrm{4}\pi} \frac{\mid{sin}\left({x}\right)\mid}{{x}}\:{dx} \\ $$$$ \\ $$

  Pg 561      Pg 562      Pg 563      Pg 564      Pg 565      Pg 566      Pg 567      Pg 568      Pg 569      Pg 570   

Terms of Service

Privacy Policy

Contact: info@tinkutara.com