
AllQuestion and Answers: Page 565
Question Number 163618 Answers: 0 Comments: 0

Question Number 163613 Answers: 0 Comments: 0

Question Number 163614 Answers: 0 Comments: 0
$$\int\frac{{sec}^{\mathrm{2}} {x}}{\left({secx}+{tanx}\right)^{\mathrm{9}/\mathrm{2}} }{dx} \\ $$
Question Number 163611 Answers: 1 Comments: 0

Question Number 163610 Answers: 1 Comments: 0
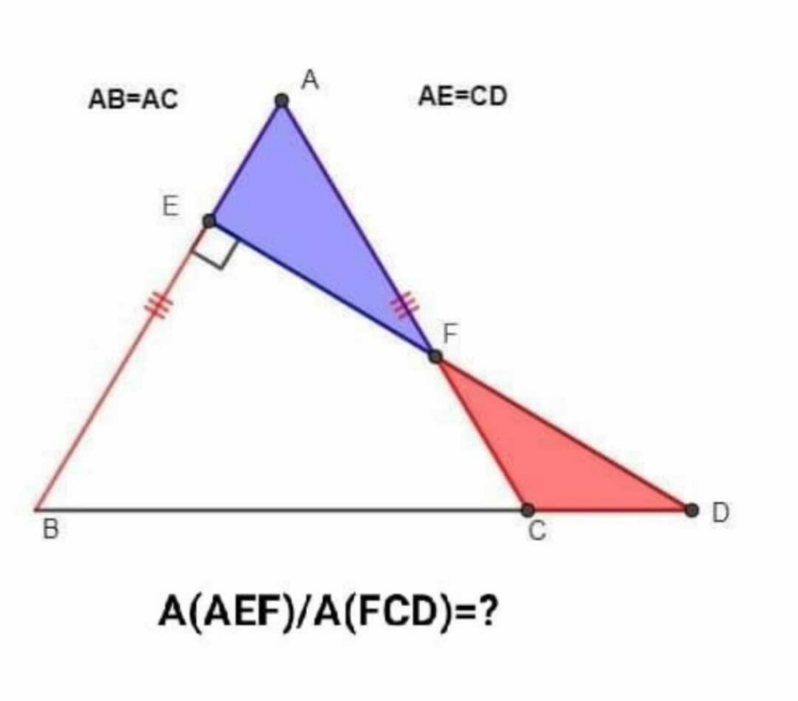
Question Number 163609 Answers: 0 Comments: 0
Question Number 163608 Answers: 0 Comments: 0
Question Number 163601 Answers: 0 Comments: 0
Question Number 163600 Answers: 1 Comments: 0
Question Number 163591 Answers: 0 Comments: 3
Question Number 163586 Answers: 0 Comments: 0
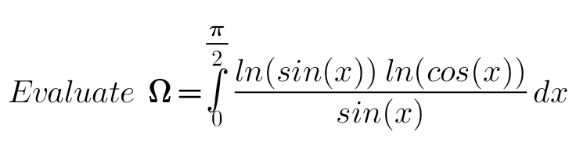
Question Number 163587 Answers: 1 Comments: 0

Question Number 163588 Answers: 0 Comments: 0
Question Number 163582 Answers: 1 Comments: 0
Question Number 163770 Answers: 2 Comments: 0
Question Number 163769 Answers: 0 Comments: 0
Question Number 163767 Answers: 0 Comments: 0
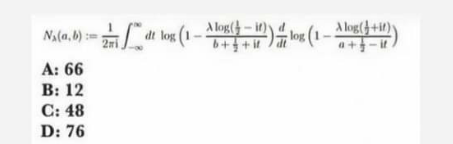
Question Number 163580 Answers: 1 Comments: 1
Question Number 163577 Answers: 0 Comments: 0
Question Number 163576 Answers: 2 Comments: 0
Question Number 163574 Answers: 1 Comments: 0
Question Number 163573 Answers: 0 Comments: 1

Question Number 163564 Answers: 0 Comments: 0
Question Number 163658 Answers: 2 Comments: 0
Question Number 163657 Answers: 2 Comments: 0
Question Number 163656 Answers: 1 Comments: 0

Pg 560 Pg 561 Pg 562 Pg 563 Pg 564 Pg 565 Pg 566 Pg 567 Pg 568 Pg 569
