
AllQuestion and Answers: Page 564
Question Number 163730 Answers: 2 Comments: 0
Question Number 163720 Answers: 1 Comments: 0
Question Number 163719 Answers: 1 Comments: 0
Question Number 163718 Answers: 0 Comments: 0
Question Number 163715 Answers: 0 Comments: 0
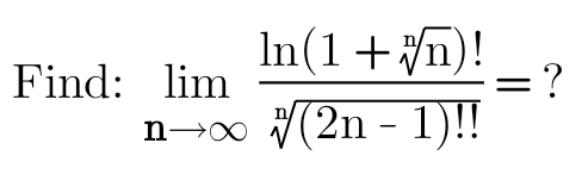
Question Number 163709 Answers: 1 Comments: 0
Question Number 163707 Answers: 0 Comments: 0
Question Number 163704 Answers: 2 Comments: 0
Question Number 163700 Answers: 3 Comments: 0
Question Number 163692 Answers: 1 Comments: 0
Question Number 163690 Answers: 1 Comments: 0
Question Number 163688 Answers: 2 Comments: 0
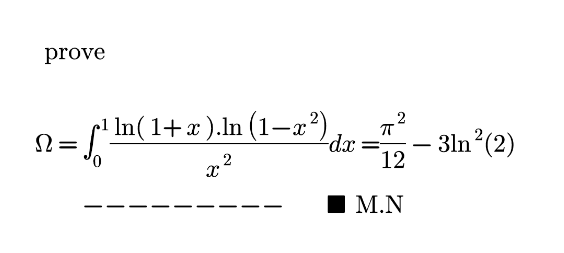
Question Number 163687 Answers: 0 Comments: 0

Question Number 163682 Answers: 1 Comments: 0
Question Number 163675 Answers: 0 Comments: 1
Question Number 163666 Answers: 4 Comments: 0
Question Number 163662 Answers: 1 Comments: 1

Question Number 163651 Answers: 1 Comments: 1
Question Number 163650 Answers: 1 Comments: 2
Question Number 163642 Answers: 1 Comments: 0
Question Number 163638 Answers: 0 Comments: 2
Question Number 163632 Answers: 2 Comments: 0
Question Number 163631 Answers: 2 Comments: 0
Question Number 163627 Answers: 2 Comments: 0

Question Number 163624 Answers: 1 Comments: 0
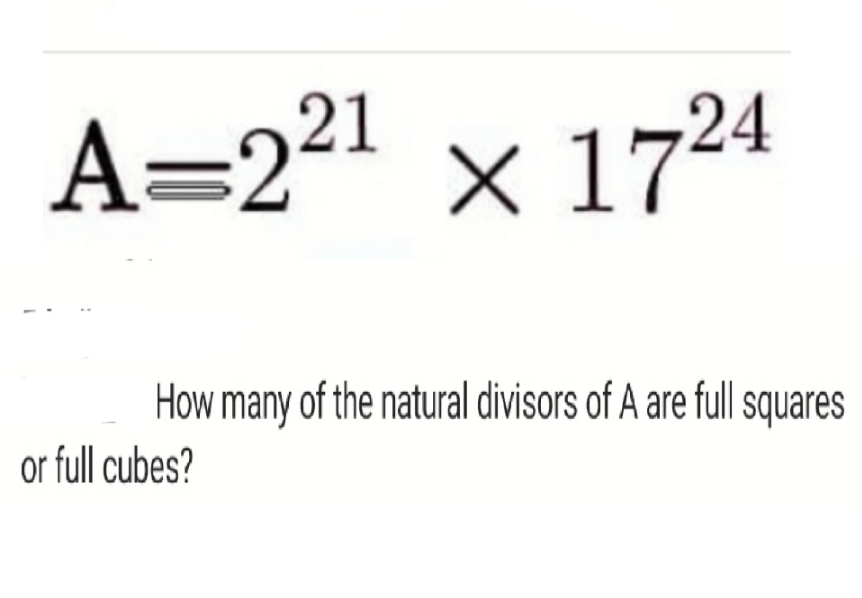
Question Number 163619 Answers: 1 Comments: 2
Pg 559 Pg 560 Pg 561 Pg 562 Pg 563 Pg 564 Pg 565 Pg 566 Pg 567 Pg 568
