Question and Answers Forum

AllQuestion and Answers: Page 563

Question Number 160493 Answers: 1 Comments: 0

montrer a l aide de binome de newton que: Σ_(k=o) ^r (^n _k )(_(r−k) ^m )=(_( r) ^(m+n) )

$${montrer}\:{a}\:{l}\:{aide}\:{de}\:{binome}\:{de}\:{newton}\:{que}:\: \\ $$$$\underset{{k}={o}} {\overset{{r}} {\sum}}\left(\underset{{k}} {\:}^{{n}} \right)\left(_{{r}−{k}} ^{{m}} \right)=\left(_{\:\:\:\:\:{r}} ^{{m}+{n}} \right)\: \\ $$

Question Number 160491 Answers: 0 Comments: 1

Question Number 160487 Answers: 3 Comments: 0

Question Number 160482 Answers: 2 Comments: 1

Question Number 160473 Answers: 1 Comments: 0

Question Number 160466 Answers: 0 Comments: 0

Question Number 160457 Answers: 2 Comments: 0

Simplfy: ((1 + cos𝛂)/(sin^2 𝛂)) : (1 + (((1 + cos𝛂)/(sin𝛂)))^2 )

$$\mathrm{Simplfy}: \\ $$$$\frac{\mathrm{1}\:+\:\mathrm{cos}\boldsymbol{\alpha}}{\mathrm{sin}^{\mathrm{2}} \boldsymbol{\alpha}}\::\:\left(\mathrm{1}\:+\:\left(\frac{\mathrm{1}\:+\:\mathrm{cos}\boldsymbol{\alpha}}{\mathrm{sin}\boldsymbol{\alpha}}\right)^{\mathrm{2}} \right) \\ $$

Question Number 160451 Answers: 2 Comments: 0

Solve the differential system below: { ((y_1 ′=2y_1 +y_2 +y_3 )),((y_2 ′=−2y_1 −y_3 )),((y_3 ′=2y_1 +y_2 +2y_3 )) :}

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{differential}\:\mathrm{system}\:\mathrm{below}: \\ $$$$\begin{cases}{{y}_{\mathrm{1}} '=\mathrm{2}{y}_{\mathrm{1}} +{y}_{\mathrm{2}} +{y}_{\mathrm{3}} }\\{{y}_{\mathrm{2}} '=−\mathrm{2}{y}_{\mathrm{1}} −{y}_{\mathrm{3}} }\\{{y}_{\mathrm{3}} '=\mathrm{2}{y}_{\mathrm{1}} +{y}_{\mathrm{2}} +\mathrm{2}{y}_{\mathrm{3}} }\end{cases} \\ $$

Question Number 160445 Answers: 1 Comments: 2

Find: ((√2)/2) ∙ ((√(2 + (√2)))/2) ∙ ((√(2 + (√(2 + (√2)))))/2) ∙ ... = ?

$$\mathrm{Find}: \\ $$$$\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\centerdot\:\frac{\sqrt{\mathrm{2}\:+\:\sqrt{\mathrm{2}}}}{\mathrm{2}}\:\centerdot\:\frac{\sqrt{\mathrm{2}\:+\:\sqrt{\mathrm{2}\:+\:\sqrt{\mathrm{2}}}}}{\mathrm{2}}\:\centerdot\:...\:=\:? \\ $$

Question Number 160444 Answers: 2 Comments: 0

Find: lim_(x→2) ((Γ((1/x) + 1) - ((√π)/x))/(x^3 - 8)) = ?

$$\mathrm{Find}:\:\:\:\underset{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{x}}\:+\:\mathrm{1}\right)\:-\:\frac{\sqrt{\pi}}{\mathrm{x}}}{\mathrm{x}^{\mathrm{3}} \:-\:\mathrm{8}}\:=\:? \\ $$

Question Number 160436 Answers: 0 Comments: 0

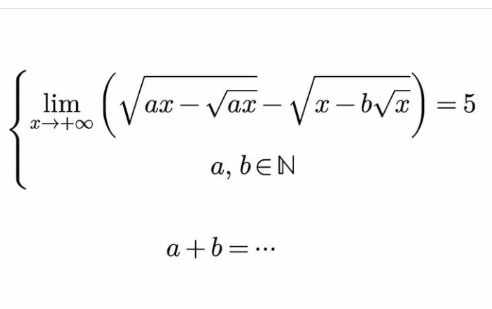
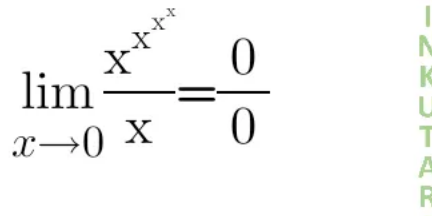
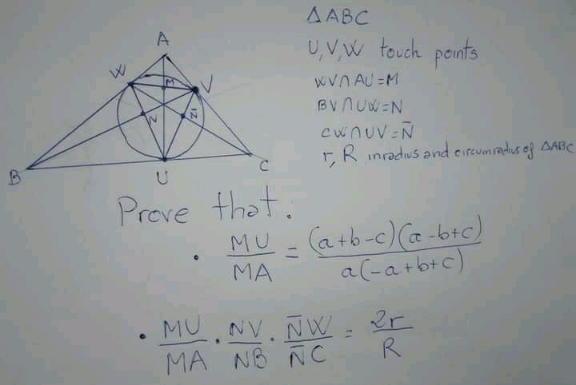
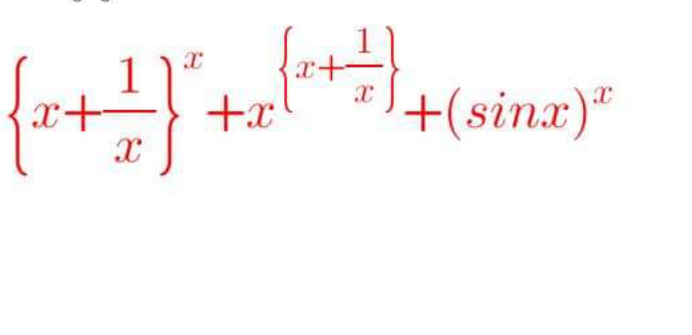
Question Number 160501 Answers: 1 Comments: 1

Calculate 1) lim_(x→1) ((cos ((Π/2))x)/(1−(√x))) 2) lim_(x→+∞) (e^(1+x) /((1+x)^x ))−(x/e)

$${Calculate} \\ $$$$\left.\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{cos}\:\left(\frac{\Pi}{\mathrm{2}}\right){x}}{\mathrm{1}−\sqrt{{x}}} \\ $$$$\left.\mathrm{2}\right)\:\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\frac{{e}^{\mathrm{1}+{x}} }{\left(\mathrm{1}+{x}\right)^{{x}} }−\frac{{x}}{{e}} \\ $$

Question Number 160431 Answers: 0 Comments: 0

∫ e^y tany dy

$$\int\:{e}^{{y}} \:{tany}\:{dy}\: \\ $$

Question Number 160432 Answers: 1 Comments: 0

∫ (dx/(sinx+cosx+1))

$$\int\:\frac{{dx}}{{sinx}+{cosx}+\mathrm{1}} \\ $$

Question Number 160427 Answers: 1 Comments: 0

lim_(n→∞) ∫_0 ^1 Σ_(i=1) ^n ((Π_(j=1) ^n (x+(j/n^2 )))/(x+(i/n^2 )))dx=?

$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\mathrm{1}} \underset{\mathrm{i}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\underset{\mathrm{j}=\mathrm{1}} {\overset{\mathrm{n}} {\prod}}\left(\mathrm{x}+\frac{\mathrm{j}}{\mathrm{n}^{\mathrm{2}} }\right)}{\mathrm{x}+\frac{\mathrm{i}}{\mathrm{n}^{\mathrm{2}} }}\mathrm{dx}=? \\ $$

Question Number 160426 Answers: 0 Comments: 2

Question Number 160424 Answers: 1 Comments: 0

Question Number 160420 Answers: 0 Comments: 0

Question Number 160416 Answers: 0 Comments: 5

guys help what does ∐ mean?

$${guys}\:{help} \\ $$$${what}\:{does}\:\coprod\:{mean}? \\ $$

Question Number 160415 Answers: 1 Comments: 0

∫_0 ^∞ (t^n /(1+t+t^2 ))dt=?

$$\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{\mathrm{t}}^{\boldsymbol{\mathrm{n}}} }{\mathrm{1}+\boldsymbol{\mathrm{t}}+\boldsymbol{\mathrm{t}}^{\mathrm{2}} }\boldsymbol{\mathrm{dt}}=? \\ $$

Question Number 160440 Answers: 0 Comments: 0

lim_(n→∞) ((√(n^2 +n))+nΣ_(k=1) ^n cos ((kπ)/n))=?

$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left(\sqrt{\mathrm{n}^{\mathrm{2}} +\mathrm{n}}+\mathrm{n}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{cos}\:\frac{\mathrm{k}\pi}{\mathrm{n}}\right)=? \\ $$

Question Number 160439 Answers: 0 Comments: 0

lim_(n→∞) ((1/(3π))∫_π ^(2π) (x/(arctan (nx)))dx)^n =?

$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{3}\pi}\int_{\pi} ^{\mathrm{2}\pi} \frac{\mathrm{x}}{\mathrm{arctan}\:\left(\mathrm{nx}\right)}\mathrm{dx}\right)^{\mathrm{n}} =? \\ $$

Question Number 160438 Answers: 0 Comments: 0

lim_(n→∞) (((2(n)^(1/n) −(2)^(1/n) )^n )/n^2 )=?

$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\mathrm{2}\sqrt[{\mathrm{n}}]{\mathrm{n}}−\sqrt[{\mathrm{n}}]{\mathrm{2}}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }=? \\ $$

Question Number 160411 Answers: 1 Comments: 0

Show that tan 58°tan 32° = 1

$$\:\:\mathrm{Show}\:\mathrm{that}\:\:\mathrm{tan}\:\mathrm{58}°\mathrm{tan}\:\mathrm{32}°\:=\:\mathrm{1} \\ $$

Question Number 160405 Answers: 1 Comments: 1

1+(1/(1+(2/(1+(1/(1+(2/(1+(1/(....)))))))))) ⇒ x^2 = ?

$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{1}+\frac{\mathrm{1}}{....}}}}}\:\:\:\Rightarrow\:\:\mathrm{x}^{\mathrm{2}} \:=\:? \\ $$

Question Number 160409 Answers: 0 Comments: 0

Pg 558 Pg 559 Pg 560 Pg 561 Pg 562 Pg 563 Pg 564 Pg 565 Pg 566 Pg 567

Contact: info@tinkutara.com