
AllQuestion and Answers: Page 562
Question Number 163914 Answers: 0 Comments: 0

Question Number 163913 Answers: 0 Comments: 0

Question Number 163912 Answers: 0 Comments: 1

Question Number 163906 Answers: 1 Comments: 0
Question Number 163905 Answers: 0 Comments: 0
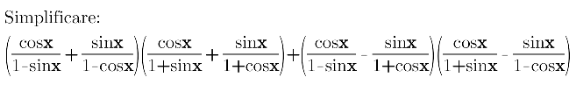
Question Number 163903 Answers: 0 Comments: 0
$${prouve}\: \\ $$$${a}/{bc}\:,{si}\:\left({a},{b}\right)=\mathrm{1},{alors} \\ $$$${a}/{c} \\ $$
Question Number 163902 Answers: 1 Comments: 0
Question Number 163899 Answers: 2 Comments: 0
Question Number 163897 Answers: 2 Comments: 0
Question Number 163891 Answers: 2 Comments: 0
Question Number 163888 Answers: 1 Comments: 1
Question Number 163886 Answers: 1 Comments: 2
Question Number 163885 Answers: 0 Comments: 0
Question Number 163881 Answers: 1 Comments: 0
Question Number 163865 Answers: 2 Comments: 0

Question Number 163861 Answers: 1 Comments: 0
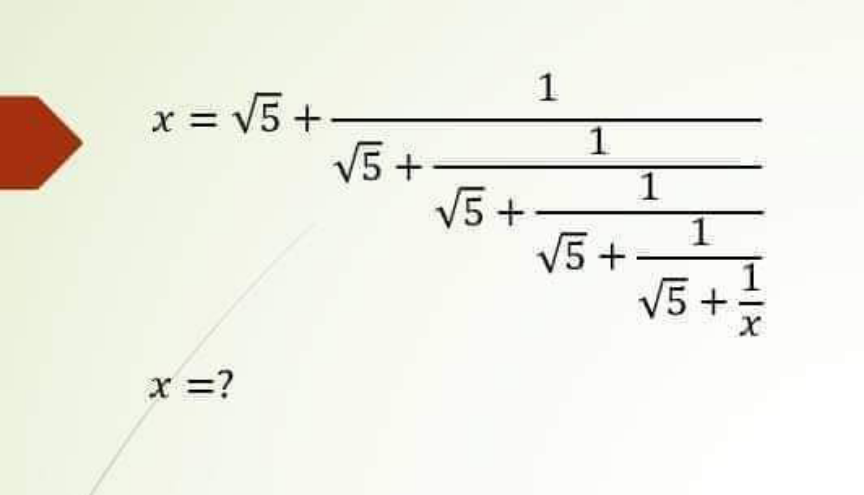
Question Number 163860 Answers: 1 Comments: 0

Question Number 163856 Answers: 1 Comments: 0
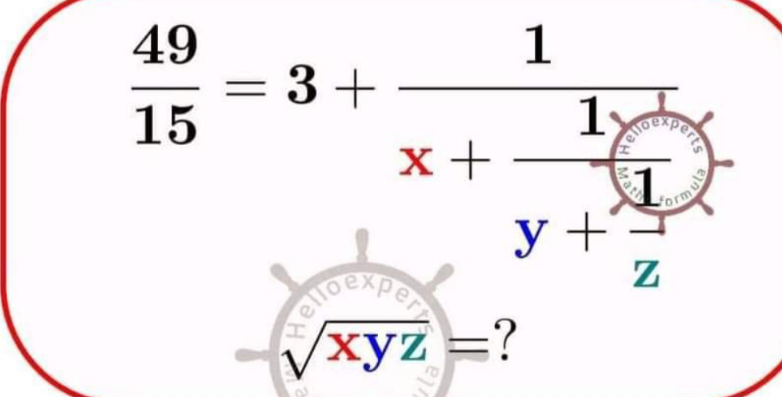
Question Number 163858 Answers: 0 Comments: 2
Question Number 163854 Answers: 1 Comments: 0
Question Number 163849 Answers: 1 Comments: 0
Question Number 163843 Answers: 0 Comments: 0

Question Number 163844 Answers: 0 Comments: 0

Question Number 163842 Answers: 1 Comments: 0
Question Number 163836 Answers: 0 Comments: 0
Question Number 163838 Answers: 0 Comments: 0

Pg 557 Pg 558 Pg 559 Pg 560 Pg 561 Pg 562 Pg 563 Pg 564 Pg 565 Pg 566
