Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 559

Question Number 160917 Answers: 1 Comments: 0

Calculate a)lim_(x→+∞) (((x−1)/(x+1)))^x^2 b) lim_(x→0) ((2^(1/x) −1)/(2^(1/x) +1))

$${Calculate} \\ $$$$\left.{a}\right)\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)^{{x}^{\mathrm{2}} } \\ $$$$\left.{b}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}^{\frac{\mathrm{1}}{{x}}} −\mathrm{1}}{\mathrm{2}^{\frac{\mathrm{1}}{{x}}} +\mathrm{1}} \\ $$

Question Number 160912 Answers: 1 Comments: 0

lim_(x→0) ((tan (x+2)tan (2−x)−tan^2 (2))/(3x tan x)) =?

$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\left(\mathrm{x}+\mathrm{2}\right)\mathrm{tan}\:\left(\mathrm{2}−\mathrm{x}\right)−\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{3x}\:\mathrm{tan}\:\mathrm{x}}\:=? \\ $$

Question Number 160910 Answers: 1 Comments: 0

Question Number 160909 Answers: 2 Comments: 0

How many 3−digits number such that sum of its digits is 11 ?

$${How}\:\:{many}\:\:\mathrm{3}−{digits}\:\:{number}\:\:{such}\:\:{that}\:\:{sum}\:\:{of}\:\:{its}\:\:{digits}\:\:{is}\:\:\mathrm{11}\:? \\ $$

Question Number 160908 Answers: 0 Comments: 1

x,y,z ∈ R^+ Find the minimum value of this expression ((xyz)/((1+3x)(x+8y)(y+9z)(6+z)))

$${x},{y},{z}\:\:\in\:\:\mathbb{R}^{+} \\ $$$${Find}\:\:{the}\:\:{minimum}\:\:{value}\:\:{of}\:\:{this}\:\:{expression}\: \\ $$$$\:\:\:\:\:\:\frac{{xyz}}{\left(\mathrm{1}+\mathrm{3}{x}\right)\left({x}+\mathrm{8}{y}\right)\left({y}+\mathrm{9}{z}\right)\left(\mathrm{6}+{z}\right)}\:\: \\ $$$$ \\ $$

Question Number 160906 Answers: 0 Comments: 0

Question Number 160903 Answers: 2 Comments: 0

(1+x^2 )y ′= 2xy +(1+x^2 )^2

$$\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}\:'=\:\mathrm{2}{xy}\:+\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} \: \\ $$

Question Number 160902 Answers: 1 Comments: 0

∫ (dx/( (√(sin^3 x)) (√(cos^5 x)))) =?

$$\:\:\int\:\frac{{dx}}{\:\sqrt{\mathrm{sin}\:^{\mathrm{3}} {x}}\:\sqrt{\mathrm{cos}\:^{\mathrm{5}} {x}}}\:=? \\ $$

Question Number 160900 Answers: 0 Comments: 2

Calculate 1) lim_(x→0) (((x+1)/(2x+1)))^x^2 lim_(x→a) (((sin x)/(sin a)))^(1/(x−a))

$${Calculate} \\ $$$$\left.\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{{x}+\mathrm{1}}{\mathrm{2}{x}+\mathrm{1}}\right)^{{x}^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:{a}}\right)^{\frac{\mathrm{1}}{{x}−{a}}} \\ $$

Question Number 160895 Answers: 1 Comments: 0

Prove that: ∫_( 0) ^( 1) ((ln(x))/(x^n + x^(n-1) + ... + 1)) dx = (1/n^2 ) [𝛙^((1)) ((2/n)) - 𝛙^((1)) ((1/n))]

$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\underset{\:\mathrm{0}} {\overset{\:\mathrm{1}} {\int}}\:\frac{\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{x}^{\boldsymbol{\mathrm{n}}} \:+\:\mathrm{x}^{\boldsymbol{\mathrm{n}}-\mathrm{1}} \:+\:...\:+\:\mathrm{1}}\:\mathrm{dx}\:=\:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\:\left[\boldsymbol{\psi}^{\left(\mathrm{1}\right)} \left(\frac{\mathrm{2}}{\mathrm{n}}\right)\:-\:\boldsymbol{\psi}^{\left(\mathrm{1}\right)} \left(\frac{\mathrm{1}}{\mathrm{n}}\right)\right] \\ $$

Question Number 160894 Answers: 1 Comments: 0

Question Number 160886 Answers: 0 Comments: 0

a_n is root of equation x^n +x=1,a_n ∈(0,1). Find lim_(n→∞) ((n−na_n −lnn)/(ln(lnn)))=?

$$\mathrm{a}_{\mathrm{n}} \:\mathrm{is}\:\mathrm{root}\:\mathrm{of}\:\mathrm{equation}\:\mathrm{x}^{\mathrm{n}} +\mathrm{x}=\mathrm{1},\mathrm{a}_{\mathrm{n}} \in\left(\mathrm{0},\mathrm{1}\right). \\ $$$$\mathrm{Find}\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{n}−\mathrm{na}_{\mathrm{n}} −\mathrm{lnn}}{\mathrm{ln}\left(\mathrm{lnn}\right)}=? \\ $$

Question Number 160885 Answers: 0 Comments: 0

lim_(n→∞) Σ_(k=1) ^n ((n+(1/k))/( (√(n^2 +k^2 ))))∙sin (1/n)=?

$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{n}+\frac{\mathrm{1}}{\mathrm{k}}}{\:\sqrt{\mathrm{n}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} }}\centerdot\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{n}}=? \\ $$

Question Number 160883 Answers: 1 Comments: 0

(√(x+1)) = ((x^2 −x−2 ((2x+1))^(1/3) )/( ((2x+1))^(1/3) −3 )) x ∈R

$$\:\sqrt{\mathrm{x}+\mathrm{1}}\:=\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{2}\:\sqrt[{\mathrm{3}}]{\mathrm{2x}+\mathrm{1}}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2x}+\mathrm{1}}\:−\mathrm{3}\:}\: \\ $$$$\:\mathrm{x}\:\in\mathbb{R}\: \\ $$

Question Number 160875 Answers: 1 Comments: 0

lim_(n→∞) ((5^n +7^n ))^(1/n) =?

$$\:\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\sqrt[{\mathrm{n}}]{\mathrm{5}^{\mathrm{n}} +\mathrm{7}^{\mathrm{n}} }\:=? \\ $$

Question Number 160873 Answers: 2 Comments: 0

Question Number 160871 Answers: 1 Comments: 0

(((2 (((2(√(13))+5)/( (√5)+2)))^(1/3) +2 (((2(√(13))−5)/( (√5)−2)))^(1/3) +1)^2 −1))^(1/6) =?

$$\:\:\sqrt[{\mathrm{6}}]{\left(\mathrm{2}\:\sqrt[{\mathrm{3}}]{\frac{\mathrm{2}\sqrt{\mathrm{13}}+\mathrm{5}}{\:\sqrt{\mathrm{5}}+\mathrm{2}}}\:+\mathrm{2}\:\sqrt[{\mathrm{3}}]{\frac{\mathrm{2}\sqrt{\mathrm{13}}−\mathrm{5}}{\:\sqrt{\mathrm{5}}−\mathrm{2}}}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}=? \\ $$

Question Number 160869 Answers: 0 Comments: 2

Find: 𝛀 =∫_( 0) ^( ∞) ((x ln (1 + x))/((x + 1)(x^2 + 1))) dx = ?

$$\mathrm{Find}: \\ $$$$\boldsymbol{\Omega}\:=\underset{\:\mathrm{0}} {\overset{\:\infty} {\int}}\:\frac{\mathrm{x}\:\mathrm{ln}\:\left(\mathrm{1}\:+\:\mathrm{x}\right)}{\left(\mathrm{x}\:+\:\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{1}\right)}\:\mathrm{dx}\:=\:? \\ $$

Question Number 160867 Answers: 0 Comments: 0

A piece of metal in the form of an equilateral triangle that has been subjected to hammering, and its circumference expands at a rate of 6 cm/s so that it remains preserved in its shape. The rate of change in its area when its side length is 12 cm

$$ \\ $$A piece of metal in the form of an equilateral triangle that has been subjected to hammering, and its circumference expands at a rate of 6 cm/s so that it remains preserved in its shape. The rate of change in its area when its side length is 12 cm

Question Number 160866 Answers: 0 Comments: 0

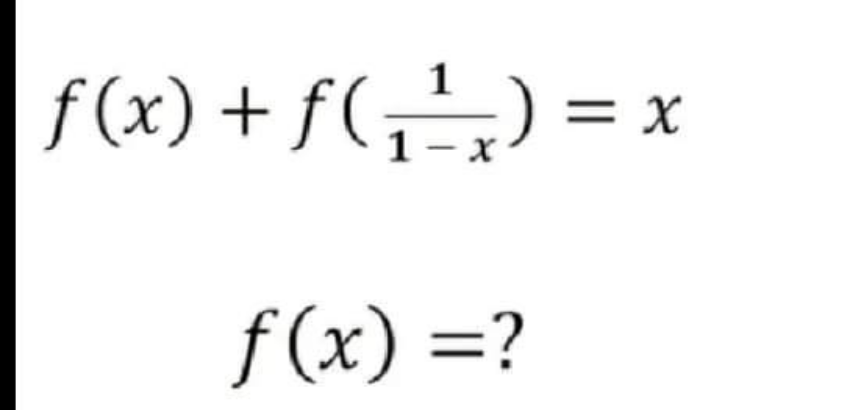
Question Number 160865 Answers: 0 Comments: 1

lim_(x→3) ((tan(x)−tan(3))/(sin(ln(x−2)))) work with the rule of substitution of infinitely small functions equivalent to a limit

$$\underset{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{3}} {\boldsymbol{\mathrm{lim}}}\frac{\boldsymbol{{tan}}\left(\boldsymbol{{x}}\right)−\boldsymbol{{tan}}\left(\mathrm{3}\right)}{\boldsymbol{{sin}}\left(\boldsymbol{{ln}}\left(\boldsymbol{{x}}−\mathrm{2}\right)\right)} \\ $$$$\boldsymbol{{work}}\:\boldsymbol{{with}}\:{the}\:{rule}\:{of} \\ $$$${substitution}\:\:{of}\:{infinitely} \\ $$$${small}\:\:{functions}\:{equivalent}\: \\ $$$${to}\:{a}\:{limit} \\ $$

Question Number 160853 Answers: 1 Comments: 1

Question Number 160852 Answers: 0 Comments: 0

Question Number 160848 Answers: 2 Comments: 0

Find the value of a such that −2 < ((2x+a)/(x^2 +1)) < 2

$${Find}\:\:{the}\:\:{value}\:\:{of}\:\:{a}\:\:{such}\:\:{that} \\ $$$$\:\:\:\:\:−\mathrm{2}\:<\:\frac{\mathrm{2}{x}+{a}}{{x}^{\mathrm{2}} +\mathrm{1}}\:<\:\mathrm{2} \\ $$

Question Number 160844 Answers: 1 Comments: 0

Question Number 160839 Answers: 2 Comments: 1

Pg 554 Pg 555 Pg 556 Pg 557 Pg 558 Pg 559 Pg 560 Pg 561 Pg 562 Pg 563

Terms of Service

Contact: info@tinkutara.com