
AllQuestion and Answers: Page 556
Question Number 164543 Answers: 1 Comments: 0
Question Number 164538 Answers: 0 Comments: 0

Question Number 164533 Answers: 2 Comments: 0
Question Number 164530 Answers: 1 Comments: 1

Question Number 164524 Answers: 1 Comments: 0

Question Number 164520 Answers: 0 Comments: 0
Question Number 164542 Answers: 0 Comments: 0
Question Number 164515 Answers: 0 Comments: 3
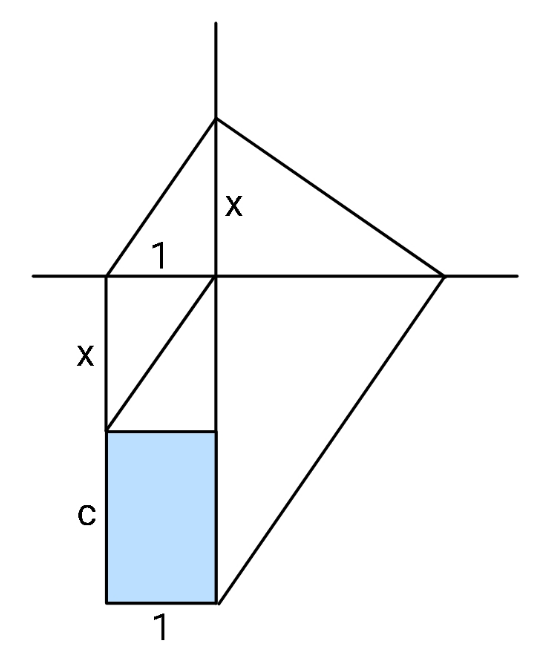
Question Number 164511 Answers: 1 Comments: 0
Question Number 164582 Answers: 0 Comments: 0

Question Number 164507 Answers: 1 Comments: 2

Question Number 164497 Answers: 1 Comments: 0

Question Number 164483 Answers: 1 Comments: 1
$$\frac{{cos}\mathrm{25}−{sin}\mathrm{65}}{{sin}\mathrm{20}+{sin}\mathrm{10}}=? \\ $$
Question Number 164488 Answers: 0 Comments: 1
Question Number 164478 Answers: 1 Comments: 0
Question Number 164477 Answers: 0 Comments: 0
Question Number 164475 Answers: 1 Comments: 0
Question Number 164474 Answers: 0 Comments: 0
Question Number 164473 Answers: 1 Comments: 0
Question Number 164462 Answers: 2 Comments: 2
Question Number 164445 Answers: 0 Comments: 1
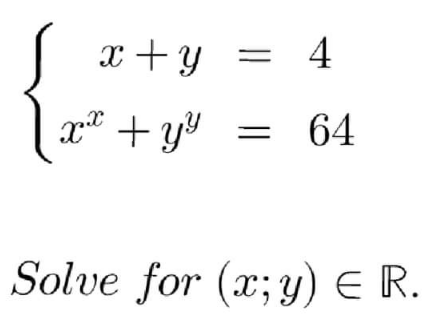
Question Number 164447 Answers: 1 Comments: 0

Question Number 164437 Answers: 1 Comments: 0
Question Number 164434 Answers: 1 Comments: 0

Question Number 164429 Answers: 1 Comments: 0
Question Number 164426 Answers: 1 Comments: 1
Pg 551 Pg 552 Pg 553 Pg 554 Pg 555 Pg 556 Pg 557 Pg 558 Pg 559 Pg 560
