
AllQuestion and Answers: Page 554
Question Number 164712 Answers: 1 Comments: 0

Question Number 164709 Answers: 1 Comments: 0

Question Number 164728 Answers: 3 Comments: 1

Question Number 164705 Answers: 2 Comments: 0
Question Number 164703 Answers: 1 Comments: 0

Question Number 164702 Answers: 1 Comments: 0
Question Number 164699 Answers: 0 Comments: 0

Question Number 164686 Answers: 1 Comments: 0
Question Number 164685 Answers: 1 Comments: 0
Question Number 164684 Answers: 1 Comments: 0
Question Number 164683 Answers: 1 Comments: 0
Question Number 164682 Answers: 1 Comments: 0
Question Number 164681 Answers: 1 Comments: 0
Question Number 164680 Answers: 0 Comments: 0
Question Number 164675 Answers: 0 Comments: 5

Question Number 164674 Answers: 0 Comments: 0

Question Number 164672 Answers: 1 Comments: 0

Question Number 164671 Answers: 1 Comments: 1
Question Number 164669 Answers: 0 Comments: 0

Question Number 164650 Answers: 1 Comments: 0
Question Number 164653 Answers: 2 Comments: 0
Question Number 164639 Answers: 1 Comments: 0

Question Number 164628 Answers: 1 Comments: 1
Question Number 164627 Answers: 1 Comments: 0

Question Number 164626 Answers: 1 Comments: 1
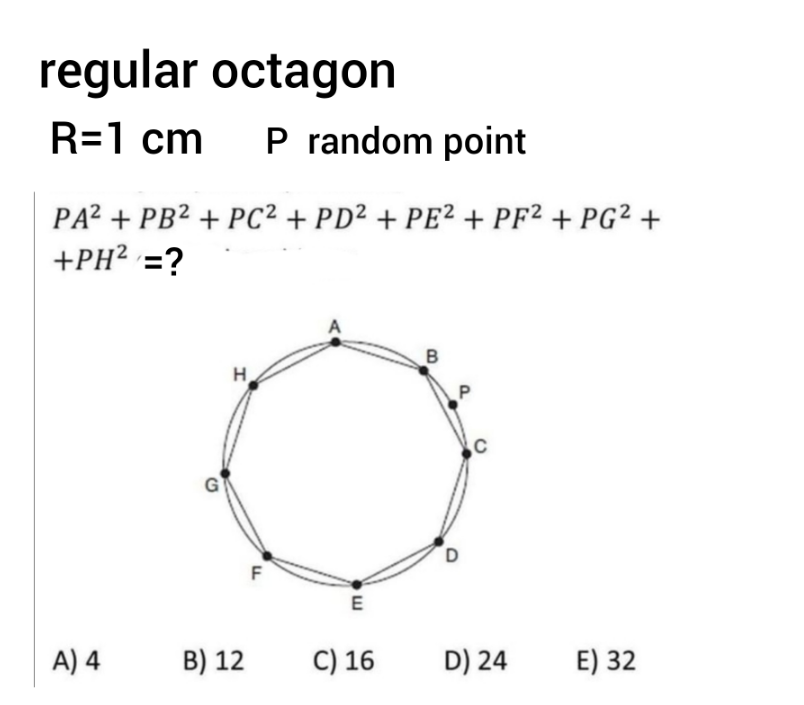
Question Number 164623 Answers: 1 Comments: 0
Pg 549 Pg 550 Pg 551 Pg 552 Pg 553 Pg 554 Pg 555 Pg 556 Pg 557 Pg 558
