
AllQuestion and Answers: Page 553
Question Number 164854 Answers: 1 Comments: 0
Question Number 164853 Answers: 0 Comments: 0
Question Number 164842 Answers: 3 Comments: 13

Question Number 164826 Answers: 2 Comments: 0
Question Number 164821 Answers: 0 Comments: 9
Question Number 164820 Answers: 1 Comments: 0
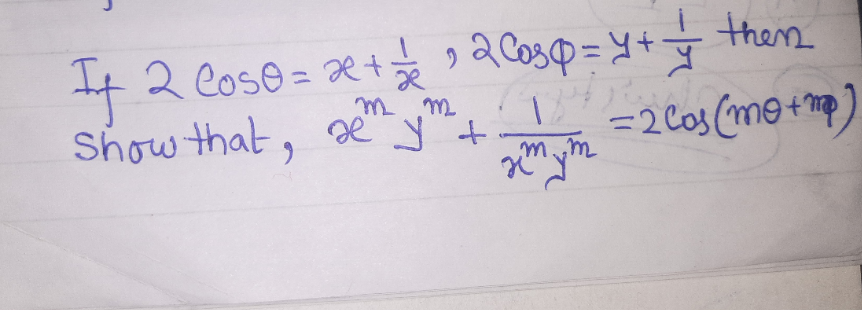
Question Number 164814 Answers: 0 Comments: 2
$${does}\:{the}\:{forum}\:{support}\:{animated} \\ $$$${images}\:{in}\:{gif}\:{format}? \\ $$
Question Number 164810 Answers: 1 Comments: 2
Question Number 164809 Answers: 2 Comments: 0
Question Number 164808 Answers: 1 Comments: 0
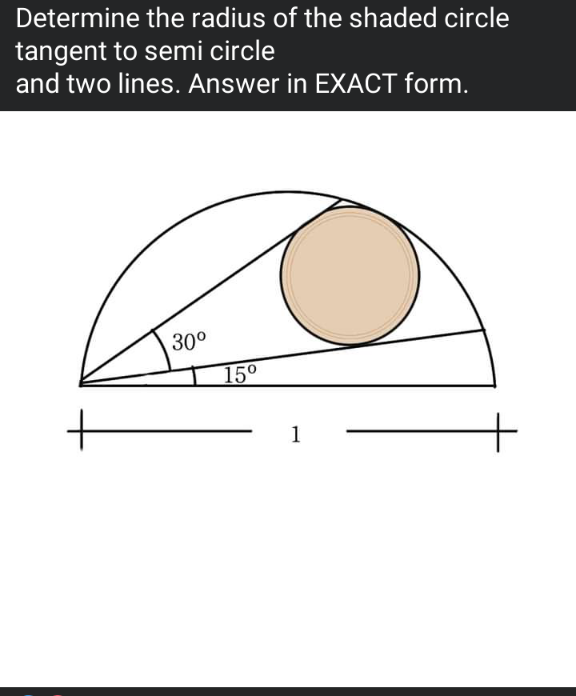
Question Number 164795 Answers: 1 Comments: 0
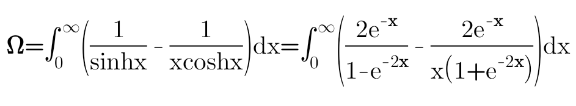
Question Number 164793 Answers: 1 Comments: 3
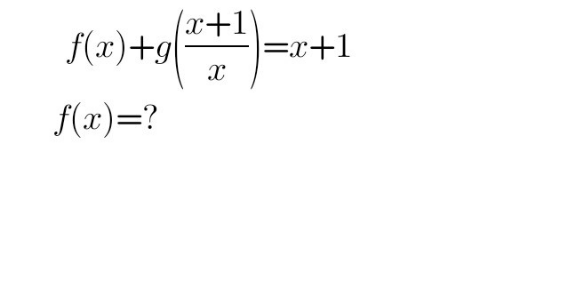
Question Number 164788 Answers: 1 Comments: 0

Question Number 164787 Answers: 2 Comments: 0

Question Number 164786 Answers: 1 Comments: 0

Question Number 164783 Answers: 1 Comments: 0
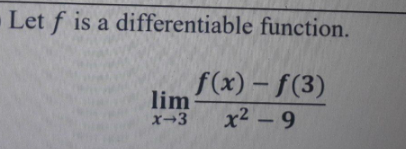
Question Number 164770 Answers: 2 Comments: 0
Question Number 164760 Answers: 2 Comments: 0
Question Number 164758 Answers: 1 Comments: 0
Question Number 164757 Answers: 0 Comments: 1
Question Number 164753 Answers: 1 Comments: 0

Question Number 164748 Answers: 0 Comments: 2

Question Number 164747 Answers: 1 Comments: 0
Question Number 164738 Answers: 0 Comments: 2

Question Number 164720 Answers: 2 Comments: 0
Question Number 164719 Answers: 0 Comments: 0

Pg 548 Pg 549 Pg 550 Pg 551 Pg 552 Pg 553 Pg 554 Pg 555 Pg 556 Pg 557
