Question and Answers Forum

AllQuestion and Answers: Page 552

Question Number 164451 Answers: 0 Comments: 1

How do you all to prove is true or false??; Prove the: (1/(1+p+p^2 +p^3 )) + (1/(1+q+q^2 +q^3 )) + (1/(1+r+r^2 +r^3 )) + (1/(1+s+s^2 +s^(3 ) )) ≥ 1

Question Number 163134 Answers: 1 Comments: 0

prove or disprove ∫_(2π) ^( 4π) (( sin(x))/x) dx >0 because ∫_(2π) ^( 3π) (( sin(x ))/x) dx > ∫_(3π) ^( 4π) ((∣sin(x)∣)/x) dx

$$ \\ $$$$\:\:\:\:{prove}\:\:{or}\:{disprove} \\ $$$$ \\ $$$$\:\:\:\:\int_{\mathrm{2}\pi} ^{\:\mathrm{4}\pi} \frac{\:{sin}\left({x}\right)}{{x}}\:{dx}\:>\mathrm{0} \\ $$$$\:\:\:\:\:\:\:{because} \\ $$$$\:\int_{\mathrm{2}\pi} ^{\:\mathrm{3}\pi} \frac{\:{sin}\left({x}\:\right)}{{x}}\:{dx}\:>\:\int_{\mathrm{3}\pi} ^{\:\mathrm{4}\pi} \frac{\mid{sin}\left({x}\right)\mid}{{x}}\:{dx} \\ $$$$ \\ $$

Question Number 163126 Answers: 0 Comments: 1

Please dear members. concerning this App How to change the color of the paper on which we are writing(for example from white to any kind of color)??????

$$\:\boldsymbol{{Please}}\:\boldsymbol{{dear}}\:\boldsymbol{{members}}.\:\boldsymbol{{concerning}}\:\boldsymbol{{this}}\:\boldsymbol{{App}} \\ $$$$\:\boldsymbol{{How}}\:\boldsymbol{{to}}\:\boldsymbol{{change}}\:\boldsymbol{{the}}\:\boldsymbol{{color}}\: \\ $$$$\:\boldsymbol{{of}}\:\boldsymbol{{the}}\:\boldsymbol{{paper}}\:\boldsymbol{{on}}\:\boldsymbol{{which}}\:\boldsymbol{{we}}\:\boldsymbol{{are}} \\ $$$$\:\boldsymbol{{writing}}\left(\boldsymbol{{for}}\:\boldsymbol{{example}}\:\boldsymbol{{from}}\:\boldsymbol{{white}}\:\boldsymbol{{to}}\:\boldsymbol{{any}}\:\boldsymbol{{kind}}\right. \\ $$$$\left.\:\:\boldsymbol{{of}}\:\boldsymbol{{color}}\right)?????? \\ $$

Question Number 163125 Answers: 0 Comments: 0

Question Number 163120 Answers: 1 Comments: 0

Question Number 163119 Answers: 2 Comments: 0

f ′(x)= f(x)+∫_0 ^1 f(x)dx f(0)=1 ⇒f(x)=?

$$\:\:{f}\:'\left({x}\right)=\:{f}\left({x}\right)+\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}\: \\ $$$$\:{f}\left(\mathrm{0}\right)=\mathrm{1}\:\Rightarrow{f}\left({x}\right)=? \\ $$

Question Number 163114 Answers: 1 Comments: 0

∫(((cos5x+cos4x)/(1+2cos3x))) dx

$$\int\left(\frac{\boldsymbol{\mathrm{cos}}\mathrm{5}\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{cos}}\mathrm{4}\boldsymbol{\mathrm{x}}}{\mathrm{1}+\mathrm{2}\boldsymbol{\mathrm{cos}}\mathrm{3}\boldsymbol{\mathrm{x}}}\right)\:\boldsymbol{\mathrm{dx}} \\ $$$$\:\: \\ $$

Question Number 163113 Answers: 0 Comments: 0

(d^2 y/dx^2 ) + ytan(x) = e^x y(0) = 1, y′(0) = 0

$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:+\:\mathrm{ytan}\left(\mathrm{x}\right)\:=\:\mathrm{e}^{\mathrm{x}} \:\:\mathrm{y}\left(\mathrm{0}\right)\:=\:\mathrm{1},\:\mathrm{y}'\left(\mathrm{0}\right)\:=\:\mathrm{0} \\ $$

Question Number 163111 Answers: 2 Comments: 0

calcul en fonction de n Σ_(k=0) ^n 3^(k−1) (_k ^n ) Σ_(k=0) ^(k=n) sin(kx)(_k ^n )

$${calcul}\:{en}\:{fonction}\:{de}\:{n} \\ $$$$\:\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{3}^{{k}−\mathrm{1}} \left(_{{k}} ^{{n}} \right) \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{k}={n}} {\sum}}{sin}\left({kx}\right)\left(_{{k}} ^{{n}} \right) \\ $$$$ \\ $$

Question Number 163098 Answers: 2 Comments: 0

Question Number 163095 Answers: 0 Comments: 2

what the best math′s app for android and pc?

$${what}\:{the}\:{best}\:{math}'{s}\:{app}\:{for}\:{android}\:{and}\:{pc}? \\ $$

Question Number 163082 Answers: 0 Comments: 3

1. u_(x x) - 2u_(x y) + 3u_(y y) - u_x = 0 2. xu_(x x) + 2xu_(x y) + 3u_(y y) + u_y = 0

$$\mathrm{1}.\:\mathrm{u}_{\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{x}}} \:-\:\mathrm{2u}_{\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{y}}} \:+\:\mathrm{3u}_{\boldsymbol{\mathrm{y}}\:\boldsymbol{\mathrm{y}}} \:-\:\mathrm{u}_{\boldsymbol{\mathrm{x}}} \:=\:\mathrm{0} \\ $$$$\mathrm{2}.\:\mathrm{xu}_{\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{x}}} \:+\:\mathrm{2xu}_{\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{y}}} \:+\:\mathrm{3u}_{\boldsymbol{\mathrm{y}}\:\boldsymbol{\mathrm{y}}} \:+\:\mathrm{u}_{\boldsymbol{\mathrm{y}}} \:=\:\mathrm{0} \\ $$

Question Number 163109 Answers: 1 Comments: 0

find the value of ∫_(−∞) ^(+∞) ((cosx)/((x^2 +1)^n ))dx (n fromN and n≥1)

$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cosx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{n}} }\mathrm{dx}\:\:\:\:\:\left(\mathrm{n}\:\mathrm{fromN}\:\mathrm{and}\:\mathrm{n}\geqslant\mathrm{1}\right) \\ $$

Question Number 163080 Answers: 1 Comments: 0

F(x)= (((x^2 −4x)^2 ))^(1/3) {: ((local maximum)),((absolut maximum)) } =?

$$\:\:\:\:\:\:\:{F}\left({x}\right)=\:\sqrt[{\mathrm{3}}]{\left({x}^{\mathrm{2}} −\mathrm{4}{x}\right)^{\mathrm{2}} }\: \\ $$$$\:\:\left.\begin{matrix}{{local}\:{maximum}}\\{{absolut}\:{maximum}}\end{matrix}\right\}\:=? \\ $$

Question Number 163099 Answers: 1 Comments: 0

1. u_(x x) = x + y 2. u_(x y) = x - y

$$\mathrm{1}.\:\mathrm{u}_{\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{x}}} \:=\:\boldsymbol{\mathrm{x}}\:+\:\boldsymbol{\mathrm{y}} \\ $$$$\mathrm{2}.\:\boldsymbol{\mathrm{u}}_{\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{y}}} \:=\:\boldsymbol{\mathrm{x}}\:-\:\boldsymbol{\mathrm{y}} \\ $$

Question Number 163101 Answers: 0 Comments: 0

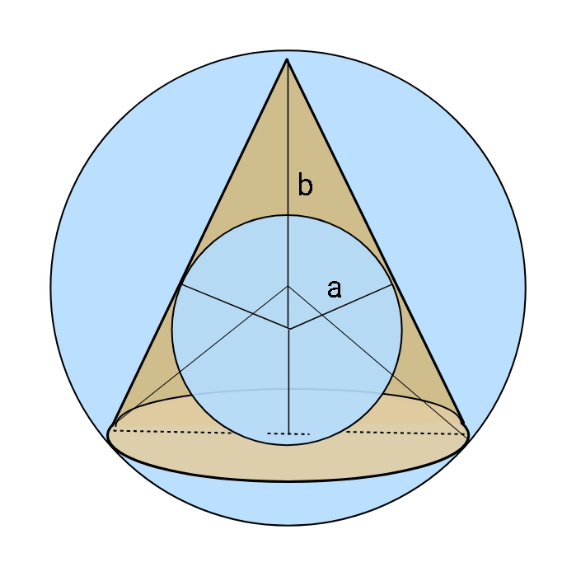
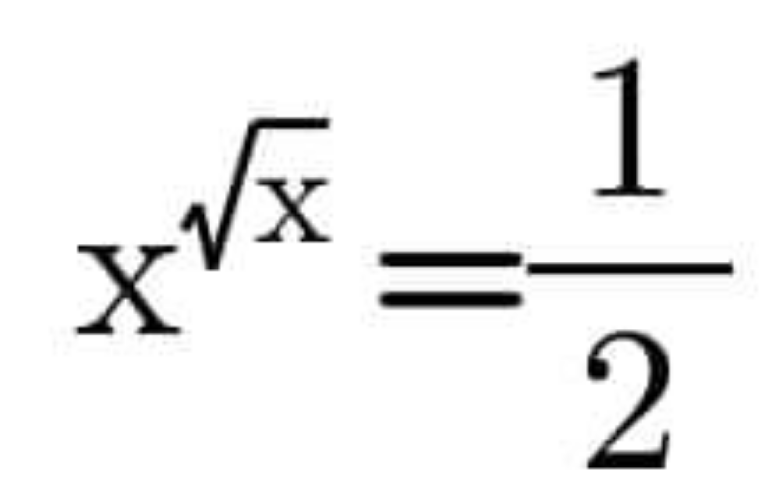
Question Number 163100 Answers: 1 Comments: 0

Question Number 163075 Answers: 2 Comments: 0

((x^3 +1)/(x^2 −1)) = x+(√(6/x))

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{x}^{\mathrm{3}} +\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}}\:=\:{x}+\sqrt{\frac{\mathrm{6}}{{x}}} \\ $$

Question Number 163061 Answers: 1 Comments: 0

(2)^(1/(log _x (((243)/x)))) = ((log _x ((x^5 /9))))^(1/3)

$$\:\sqrt[{\mathrm{log}\:_{{x}} \left(\frac{\mathrm{243}}{{x}}\right)}]{\mathrm{2}}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{log}\:_{{x}} \left(\frac{{x}^{\mathrm{5}} }{\mathrm{9}}\right)}\: \\ $$

Question Number 163060 Answers: 1 Comments: 1

2log _3 ((x^2 /(27))) = 2+ ((log _3 ((1/x)))/(log _5 ((√x) )))

$$\:\:\mathrm{2log}\:_{\mathrm{3}} \left(\frac{{x}^{\mathrm{2}} }{\mathrm{27}}\right)\:=\:\mathrm{2}+\:\frac{\mathrm{log}\:_{\mathrm{3}} \left(\frac{\mathrm{1}}{{x}}\right)}{\mathrm{log}\:_{\mathrm{5}} \left(\sqrt{{x}}\:\right)}\: \\ $$

Question Number 163053 Answers: 1 Comments: 1

Question Number 163048 Answers: 3 Comments: 0

Question Number 163045 Answers: 1 Comments: 0

prove that Σ_(n=1) ^∞ (( ( 2n+1 )!!)/((2n )!!)) (1/(2^( n) (2n +1)^( 2) )) =((π(√2))/4)−1

$$ \\ $$$$\:\:\:\:\:{prove}\:{that} \\ $$$$ \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\:\left(\:\mathrm{2}{n}+\mathrm{1}\:\right)!!}{\left(\mathrm{2}{n}\:\right)!!}\:\frac{\mathrm{1}}{\mathrm{2}^{\:{n}} \left(\mathrm{2}{n}\:+\mathrm{1}\right)^{\:\mathrm{2}} }\:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}}−\mathrm{1} \\ $$

Question Number 163043 Answers: 0 Comments: 0

lim_(x→−∞) Σ_(n=1) ^∞ (x^n /n^n )=?

$$\underset{\mathrm{x}\rightarrow−\infty} {\mathrm{lim}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}^{\mathrm{n}} }=? \\ $$

Question Number 163042 Answers: 0 Comments: 0

lim_(n→∞) (√n)∫_(−∞) ^(+∞) ((cos x)/((1+x^2 )^n ))dx=?

$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\sqrt{\mathrm{n}}\int_{−\infty} ^{+\infty} \frac{\mathrm{cos}\:\mathrm{x}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}} }\mathrm{dx}=? \\ $$

Question Number 163041 Answers: 0 Comments: 0

lim_(n→∞) (√n)(∫_0 ^1 ((1−(1−x^2 )^n )/( (√n)x^2 ))dx−(√π))=?

$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\sqrt{\mathrm{n}}\left(\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}} }{\:\sqrt{\mathrm{n}}\mathrm{x}^{\mathrm{2}} }\mathrm{dx}−\sqrt{\pi}\right)=? \\ $$

Pg 547 Pg 548 Pg 549 Pg 550 Pg 551 Pg 552 Pg 553 Pg 554 Pg 555 Pg 556

Contact: info@tinkutara.com