Question and Answers Forum

AllQuestion and Answers: Page 551

Question Number 163325 Answers: 1 Comments: 2

2a=(1/( (√1)+(√2)))+(1/( (√2)+(√3)))+...+(1/( (√(2024))+(√(2025))))=?

$$\mathrm{2}{a}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}}+\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}}+...+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2024}}+\sqrt{\mathrm{2025}}}=? \\ $$

Question Number 163324 Answers: 1 Comments: 0

Given that {a_n } is a geometric sequence where the first term, a_1 >1 and the common ratio, r>0. If b_n =log_2 a_n where n∈N, b_1 +b_3 +b_5 =6, and b_1 ∙b_3 ∙b_5 =0, find the general term of {a_n }.

$$\mathrm{Given}\:\mathrm{that}\:\left\{{a}_{{n}} \right\}\:\mathrm{is}\:\mathrm{a}\:\mathrm{geometric}\:\mathrm{sequence} \\ $$$$\mathrm{where}\:\mathrm{the}\:\mathrm{first}\:\mathrm{term},\:{a}_{\mathrm{1}} >\mathrm{1}\:\mathrm{and}\:\mathrm{the}\:\mathrm{common} \\ $$$$\mathrm{ratio},\:{r}>\mathrm{0}.\: \\ $$$$\mathrm{If}\:{b}_{{n}} =\mathrm{log}_{\mathrm{2}} \:{a}_{{n}} \:\mathrm{where}\:{n}\in\mathbb{N},\:{b}_{\mathrm{1}} +{b}_{\mathrm{3}} +{b}_{\mathrm{5}} =\mathrm{6}, \\ $$$$\mathrm{and}\:{b}_{\mathrm{1}} \centerdot{b}_{\mathrm{3}} \centerdot{b}_{\mathrm{5}} =\mathrm{0},\:\mathrm{find}\:\mathrm{the}\:\mathrm{general}\:\mathrm{term}\:\mathrm{of}\:\left\{{a}_{{n}} \right\}. \\ $$

Question Number 163323 Answers: 1 Comments: 1

Given the roots of the quadratic equation 4x^2 −4x+5=0 are α and β. f(x) is a quadratic function where f(α)=β , f(β)=α and f(0)=6 . Find f(x).

$$\mathrm{Given}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{quadratic}\:\mathrm{equation} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}=\mathrm{0}\:\mathrm{are}\:\alpha\:\mathrm{and}\:\beta.\:\: \\ $$$${f}\left({x}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{quadratic}\:\mathrm{function}\:\mathrm{where}\:{f}\left(\alpha\right)=\beta\:, \\ $$$${f}\left(\beta\right)=\alpha\:\mathrm{and}\:{f}\left(\mathrm{0}\right)=\mathrm{6}\:.\: \\ $$$$\mathrm{Find}\:{f}\left({x}\right). \\ $$

Question Number 163320 Answers: 0 Comments: 0

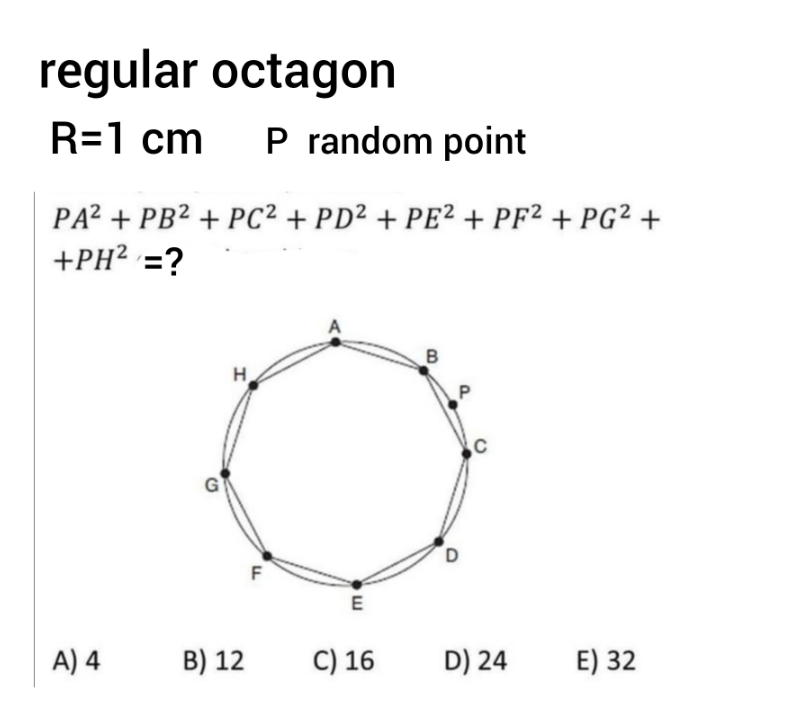
Question Number 163316 Answers: 3 Comments: 0

calculer une primitive de x:→ln(1−x^2 ) puis jusrifier la convergence de ∫_0 ^1 ln(1−x^2 )dx

$${calculer}\:{une}\:{primitive}\:{de}\:{x}:\rightarrow{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right) \\ $$$${puis}\:{jusrifier}\:{la}\:{convergence}\:{de}\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){dx} \\ $$

Question Number 163313 Answers: 1 Comments: 0

Find the non negative integer solutions of 2x+3y+5z=60

$${Find}\:{the}\:{non}\:{negative}\:{integer} \\ $$$${solutions}\:{of}\:\mathrm{2}{x}+\mathrm{3}{y}+\mathrm{5}{z}=\mathrm{60} \\ $$

Question Number 163318 Answers: 1 Comments: 0

Question Number 163300 Answers: 1 Comments: 0

∫_0 ^2 f(x)dx⋍f(a)+f(2−a) For what values of a is the following formula accurate for polynomials of degree 3?

$$\int_{\mathrm{0}} ^{\mathrm{2}} \boldsymbol{{f}}\left(\boldsymbol{{x}}\right)\boldsymbol{{dx}}\backsimeq\boldsymbol{{f}}\left(\boldsymbol{{a}}\right)+\boldsymbol{{f}}\left(\mathrm{2}−\boldsymbol{{a}}\right) \\ $$$$ \\ $$For what values of a is the following formula accurate for polynomials of degree 3?

Question Number 163292 Answers: 1 Comments: 0

Question Number 163288 Answers: 1 Comments: 0

Question Number 163285 Answers: 1 Comments: 0

# Question # suppose that x_1 , x_( 2) are two distinct roots for ax^( 2) + bx +c = 0 on ( 0, 1 ). find the minimum value of ” a ” : a_( min) = ? −−−−−−−−−

$$ \\ $$$$\:\:\:\:#\:\mathrm{Q}{uestion}\:# \\ $$$$\:\:\:\:\:{suppose}\:{that}\:\:{x}_{\mathrm{1}} \:,\:\:{x}_{\:\mathrm{2}} \:\:{are}\:{two}\:{distinct} \\ $$$$\:\:\:\:{roots}\:{for}\:\:\:{ax}^{\:\mathrm{2}} +\:{bx}\:+{c}\:=\:\mathrm{0}\:\:{on}\:\left(\:\mathrm{0},\:\mathrm{1}\:\right). \\ $$$$\:\:\:\:\:{find}\:\:{the}\:{minimum}\:{value}\:{of}\:\:''\:{a}\:''\:: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}_{\:{min}} \:=\:? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−−−−−−− \\ $$$$\:\:\:\:\:\: \\ $$

Question Number 163284 Answers: 1 Comments: 0

given 2020^x +2020^(−x) =3 (√((2020^(6x) −2020^(−6x) )/( 2020^x −2020^(−x) )))=?

$$\:{given}\:\:\mathrm{2020}^{{x}} +\mathrm{2020}^{−{x}} =\mathrm{3} \\ $$$$\:\sqrt{\frac{\mathrm{2020}^{\mathrm{6}{x}} −\mathrm{2020}^{−\mathrm{6}{x}} }{\:\mathrm{2020}^{{x}} −\mathrm{2020}^{−{x}} }}=? \\ $$

Question Number 163283 Answers: 1 Comments: 1

hi ! We store 5 objects in three discernible drawers. Suppose that the different ways of carrying out these arrangements are equally probable, calculate the probability that one of the 3 drawers contains at least 3 objects.

$$\mathrm{hi}\:! \\ $$We store 5 objects in three discernible drawers. Suppose that the different ways of carrying out these arrangements are equally probable, calculate the probability that one of the 3 drawers contains at least 3 objects.

Question Number 163280 Answers: 1 Comments: 5

Question Number 163271 Answers: 0 Comments: 0

put : gcd( a , b )= (a, b ) if ( a ,b )= (a ,c )= (b ,c )=1 prove that : (abc , ab +ac +bc )=1

$$ \\ $$$$\:\:\:\:\:\:{put}\::\:\:{gcd}\left(\:{a}\:,\:{b}\:\right)=\:\left({a},\:{b}\:\right) \\ $$$$\:\:\:\:\:\:\:{if}\:\:\:\left(\:{a}\:,{b}\:\right)=\:\left({a}\:,{c}\:\right)=\:\left({b}\:,{c}\:\right)=\mathrm{1} \\ $$$${prove}\:{that}\::\:\:\left({abc}\:,\:{ab}\:+{ac}\:+{bc}\:\right)=\mathrm{1} \\ $$$$ \\ $$

Question Number 163259 Answers: 1 Comments: 0

Question Number 163257 Answers: 0 Comments: 0

Re ( ∫_0 ^( 1) sin^( −1) ((( 1)/(1− x^( 2) )) )dx )=?

$$ \\ $$$$\:\:\:\:\:\mathscr{R}{e}\:\left(\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {sin}^{\:−\mathrm{1}} \left(\frac{\:\mathrm{1}}{\mathrm{1}−\:{x}^{\:\mathrm{2}} }\:\right){dx}\:\right)=? \\ $$$$ \\ $$

Question Number 163263 Answers: 1 Comments: 0

Question Number 163293 Answers: 1 Comments: 1

Question Number 163226 Answers: 2 Comments: 3

Question Number 163223 Answers: 1 Comments: 0

The arc of parabola y=−x^2 +9 in 0<x<3 is revolved about the line y=c and 0<c<9 to generate a solid. Find the value of c that minimizes the volume of the solid.

$$\mathrm{The}\:\mathrm{arc}\:\mathrm{of}\:\mathrm{parabola}\:{y}=−{x}^{\mathrm{2}} +\mathrm{9}\:\mathrm{in}\:\mathrm{0}<{x}<\mathrm{3} \\ $$$$\mathrm{is}\:\mathrm{revolved}\:\mathrm{about}\:\mathrm{the}\:\mathrm{line}\:{y}={c}\:\mathrm{and}\:\mathrm{0}<{c}<\mathrm{9} \\ $$$$\mathrm{to}\:\mathrm{generate}\:\mathrm{a}\:\mathrm{solid}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{c}\:\mathrm{that}\:\mathrm{minimizes}\:\mathrm{the}\: \\ $$$$\mathrm{volume}\:\mathrm{of}\:\mathrm{the}\:\mathrm{solid}. \\ $$

Question Number 163222 Answers: 1 Comments: 0

(√(((√(x+4)) +2)/(2−(√(x+4))))) ≤ x−4

$$\:\:\:\sqrt{\frac{\sqrt{{x}+\mathrm{4}}\:+\mathrm{2}}{\mathrm{2}−\sqrt{{x}+\mathrm{4}}}}\:\leqslant\:{x}−\mathrm{4}\: \\ $$

Question Number 163217 Answers: 0 Comments: 0

Question Number 163211 Answers: 0 Comments: 0

Question Number 163210 Answers: 1 Comments: 1

Question Number 163209 Answers: 0 Comments: 0

f : I → (0 ; ∞) ; I ⊂ R f - twice derivable ; f^′ ; f^(′′) - continuous f^(′′) (x) f(x) ≥ (f^′ (x))^2 ; ∀ x ∈ I then prove that: 2f (((x + y)/2)) ≤ f(x) + f(y) ; ∀ x;y ∈ I

$$\mathrm{f}\::\:\mathrm{I}\:\rightarrow\:\left(\mathrm{0}\:;\:\infty\right)\:\:;\:\:\mathrm{I}\:\subset\:\mathbb{R} \\ $$$$\mathrm{f}\:-\:\mathrm{twice}\:\mathrm{derivable}\:\:;\:\:\mathrm{f}\:^{'} \:;\:\mathrm{f}\:^{''} \:-\:\mathrm{continuous} \\ $$$$\mathrm{f}\:^{''} \left(\mathrm{x}\right)\:\mathrm{f}\left(\mathrm{x}\right)\:\geqslant\:\left(\mathrm{f}\:^{'} \left(\mathrm{x}\right)\right)^{\mathrm{2}} \:;\:\:\forall\:\mathrm{x}\:\in\:\mathrm{I} \\ $$$$\mathrm{then}\:\mathrm{prove}\:\mathrm{that}: \\ $$$$\mathrm{2f}\:\left(\frac{\mathrm{x}\:+\:\mathrm{y}}{\mathrm{2}}\right)\:\leqslant\:\mathrm{f}\left(\mathrm{x}\right)\:+\:\mathrm{f}\left(\mathrm{y}\right)\:\:;\:\:\forall\:\mathrm{x};\mathrm{y}\:\in\:\mathrm{I} \\ $$

Pg 546 Pg 547 Pg 548 Pg 549 Pg 550 Pg 551 Pg 552 Pg 553 Pg 554 Pg 555

Contact: info@tinkutara.com