
AllQuestion and Answers: Page 549
Question Number 165314 Answers: 0 Comments: 2
Question Number 165301 Answers: 1 Comments: 0

Question Number 165296 Answers: 2 Comments: 1

Question Number 165307 Answers: 0 Comments: 0

Question Number 165291 Answers: 1 Comments: 0

Question Number 165309 Answers: 0 Comments: 0
Question Number 165262 Answers: 2 Comments: 0
Question Number 165255 Answers: 1 Comments: 0
Question Number 165243 Answers: 1 Comments: 0
Question Number 165240 Answers: 1 Comments: 0
Question Number 165234 Answers: 0 Comments: 1
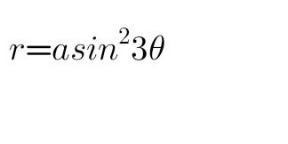
Question Number 165253 Answers: 3 Comments: 0

Question Number 165232 Answers: 1 Comments: 1
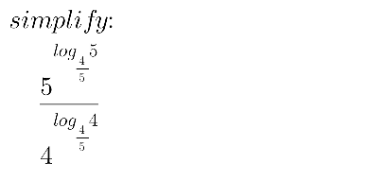
Question Number 165250 Answers: 0 Comments: 1
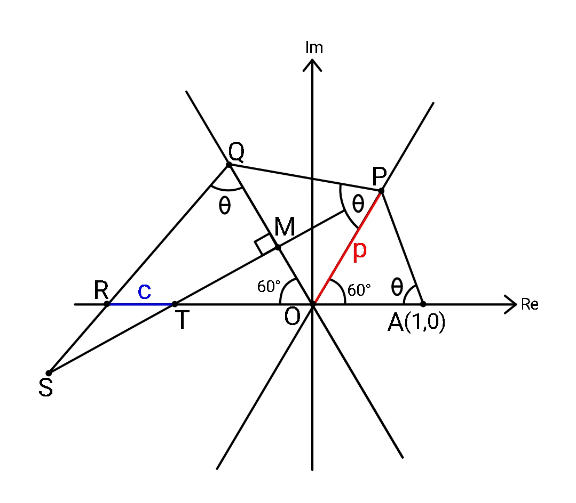
Question Number 165229 Answers: 0 Comments: 1
Question Number 165226 Answers: 1 Comments: 0
$${make}\:{x}\:{the}\:{subject}\:{of}\:{the}\:{formula}; \\ $$$${a}^{{x}} +{bx}+{c}=\mathrm{0} \\ $$
Question Number 165217 Answers: 2 Comments: 5
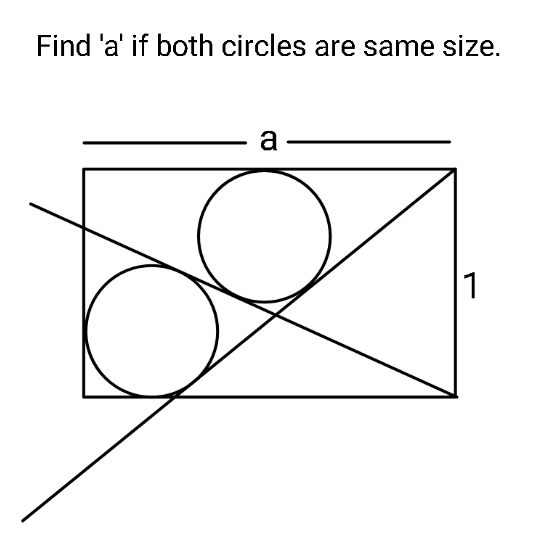
Question Number 165218 Answers: 1 Comments: 1
Question Number 165215 Answers: 1 Comments: 0
Question Number 165210 Answers: 0 Comments: 1
Question Number 165209 Answers: 0 Comments: 0
Question Number 165208 Answers: 1 Comments: 0
Question Number 165194 Answers: 2 Comments: 0
Question Number 165183 Answers: 0 Comments: 1
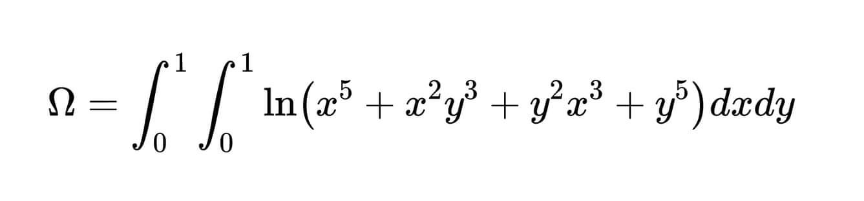
Question Number 165178 Answers: 2 Comments: 0
Question Number 165170 Answers: 2 Comments: 3

Pg 544 Pg 545 Pg 546 Pg 547 Pg 548 Pg 549 Pg 550 Pg 551 Pg 552 Pg 553
