Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 546

Question Number 163861 Answers: 1 Comments: 0

Question Number 163860 Answers: 1 Comments: 0

Question Number 163856 Answers: 1 Comments: 0

Question Number 163858 Answers: 0 Comments: 2

which object or substance has the 2rd number velocity after light?

$${which}\:{object}\:{or}\:{substance}\:{has}\:\:{the}\: \\ $$$$\mathrm{2}{rd}\:{number}\:{velocity}\:{after}\:{light}? \\ $$

Question Number 163854 Answers: 1 Comments: 0

solution with residu theorem ∫_0 ^∞ (x^2 /(x^4 +2x^2 +2))dx=?

$$\boldsymbol{\mathrm{solution}}\:\boldsymbol{\mathrm{with}}\:\boldsymbol{\mathrm{residu}}\:\boldsymbol{\mathrm{theorem}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }{\boldsymbol{\mathrm{x}}^{\mathrm{4}} +\mathrm{2}\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{2}}\boldsymbol{\mathrm{dx}}=?\:\:\:\: \\ $$

Question Number 163849 Answers: 1 Comments: 0

(1/(1 ∙ 2)) + (1/(2 ∙ 3)) + ... (1/(19 ∙ 20)) + (1/(20 ∙ 21)) = ?

$$\frac{\mathrm{1}}{\mathrm{1}\:\centerdot\:\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{2}\:\centerdot\:\mathrm{3}}\:+\:...\:\frac{\mathrm{1}}{\mathrm{19}\:\centerdot\:\mathrm{20}}\:+\:\frac{\mathrm{1}}{\mathrm{20}\:\centerdot\:\mathrm{21}}\:=\:? \\ $$

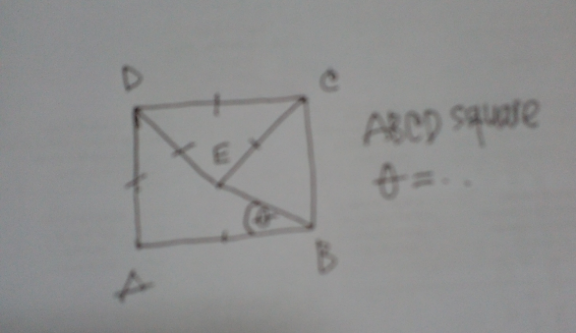
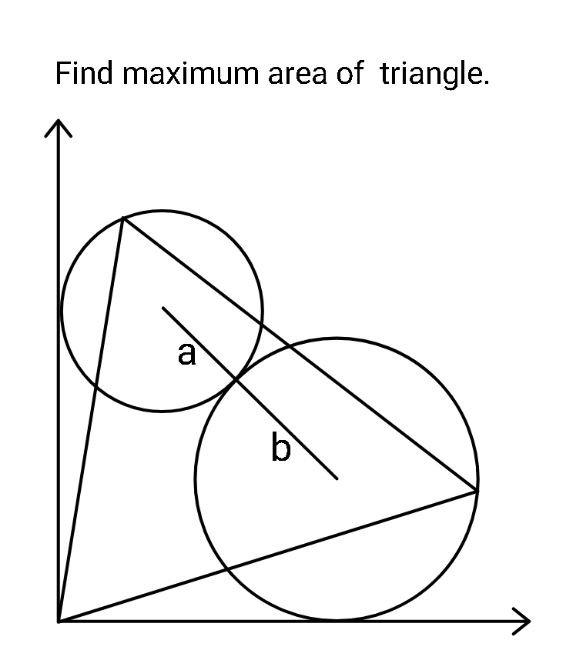
Question Number 163843 Answers: 0 Comments: 0

Question Number 163844 Answers: 0 Comments: 0

Question Number 163842 Answers: 1 Comments: 0

calculate Ω = ∫_0 ^( 1) ((( Arctanh (x))/x^ ))^( 2) dx =? −− m.n −−

$$ \\ $$$$\:\:\:\:\:\:\:{calculate} \\ $$$$\:\:\:\: \\ $$$$\:\:\Omega\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{\:\:\mathscr{A}{rctanh}\:\left({x}\right)}{{x}^{\:} }\right)^{\:\mathrm{2}} \:{dx}\:=? \\ $$$$\:\:\:\:\:\:\:\:\:−−\:{m}.{n}\:−− \\ $$

Question Number 163836 Answers: 0 Comments: 0

par recurence (4^n /(2n))<(_n ^k )<(4^n /2)

$${par}\:{recurence} \\ $$$$\frac{\mathrm{4}^{{n}} }{\mathrm{2}{n}}<\left(_{{n}} ^{{k}} \right)<\frac{\mathrm{4}^{{n}} }{\mathrm{2}} \\ $$

Question Number 163838 Answers: 0 Comments: 0

Question Number 163833 Answers: 1 Comments: 12

Question Number 163829 Answers: 3 Comments: 1

∫(1/(cos x))

$$\int\frac{\mathrm{1}}{\mathrm{cos}\:{x}} \\ $$

Question Number 163828 Answers: 2 Comments: 0

∫(e^x /x)

$$\int\frac{{e}^{{x}} }{{x}} \\ $$

Question Number 163825 Answers: 2 Comments: 0

lim_(x→0) ((tan 2x−2x)/(sin 3x−3x)) =?

$$\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\mathrm{2}{x}−\mathrm{2}{x}}{\mathrm{sin}\:\mathrm{3}{x}−\mathrm{3}{x}}\:=?\: \\ $$

Question Number 163834 Answers: 0 Comments: 0

∫_0 ^∞ ((t(e^(4t) −1)(ln(i)+t))/e^(2t) )dt=? by M.A

$$\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{t}}\left(\boldsymbol{{e}}^{\mathrm{4}\boldsymbol{{t}}} −\mathrm{1}\right)\left(\boldsymbol{{ln}}\left(\boldsymbol{{i}}\right)+\boldsymbol{{t}}\right)}{\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{t}}} }\boldsymbol{{dt}}=? \\ $$$$\boldsymbol{{by}}\:\:\boldsymbol{{M}}.\boldsymbol{{A}} \\ $$

Question Number 163822 Answers: 2 Comments: 0

sin(4x) − sin(3x) = sin(2x) find x ?

$${sin}\left(\mathrm{4}{x}\right)\:−\:{sin}\left(\mathrm{3}{x}\right)\:=\:{sin}\left(\mathrm{2}{x}\right)\:{find}\:{x}\:? \\ $$

Question Number 163812 Answers: 2 Comments: 0

Question Number 163845 Answers: 1 Comments: 0

a, b ∈ N , gcd( a , b )=1 prove that a^( ϕ (b )) + b^( ϕ (a )) ≡^( ab) 1 ϕ : Euler phi function ...

$$ \\ $$$$\:\:\:\:\:\:\:{a},\:{b}\:\in\:\mathbb{N}\:\:,\:\:{gcd}\left(\:{a}\:,\:\:{b}\:\right)=\mathrm{1} \\ $$$$\:\:\:\:\:{prove}\:\:{that}\: \\ $$$$\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{a}^{\:\:\varphi\:\left({b}\:\right)} +\:{b}^{\:\varphi\:\left({a}\:\right)} \:\overset{\:{ab}} {\equiv}\:\mathrm{1} \\ $$$$\:\:\:\:\:\varphi\::\:\:\:\mathscr{E}{uler}\:{phi}\:\:{function}\:... \\ $$$$ \\ $$

Question Number 163798 Answers: 2 Comments: 0

by a simple method calculate Σ_(k=0) ^n COS(kx)

$$ \\ $$$$\:\:\:\:{by}\:{a}\:{simple}\:{method}\:{calculate}\:\:\: \\ $$$$\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\sum_{{k}=\mathrm{0}} ^{{n}} {COS}\left({kx}\right) \\ $$$$ \\ $$$$ \\ $$

Question Number 163789 Answers: 0 Comments: 1

∫_0 ^1 ((arccotgh(x))/(1−x^2 ))dx=? by M.A

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{{arccotgh}}\left(\boldsymbol{{x}}\right)}{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }\boldsymbol{{dx}}=? \\ $$$$\boldsymbol{{by}}\:\boldsymbol{{M}}.\boldsymbol{{A}} \\ $$

Question Number 163785 Answers: 0 Comments: 0

∫_0 ^1 ((ln(x−1)ln(1−x))/x)dx=? ∫_0 ^1 ((ln(x−1)ln(1+x))/x)dx=? by M.A

Question Number 163782 Answers: 1 Comments: 1

Question Number 163786 Answers: 1 Comments: 0

Question Number 163775 Answers: 1 Comments: 1

Question Number 163763 Answers: 3 Comments: 1

$$ \\ $$

Pg 541 Pg 542 Pg 543 Pg 544 Pg 545 Pg 546 Pg 547 Pg 548 Pg 549 Pg 550

Contact: info@tinkutara.com