Question and Answers Forum

AllQuestion and Answers: Page 539

Question Number 164010 Answers: 0 Comments: 3

Question Number 164009 Answers: 2 Comments: 0

Question Number 164471 Answers: 1 Comments: 0

une primitive de ln(1−x^2 )dx puis la convergence de ∫_0 ^1 ln(1−x^2 )dx

$$\:{une}\:{primitive}\:{de}\:{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){dx} \\ $$$${puis}\:{la}\:{convergence}\:{de}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){dx} \\ $$

Question Number 164001 Answers: 1 Comments: 1

Question Number 163998 Answers: 0 Comments: 0

Hi... Calculate: ∫−(λ/(4πε_0 ))[((√(1+(πu/2)^2 ))/((1+u^2 )^(3/2) ))]du

$${Hi}... \\ $$$${Calculate}: \\ $$$$\int−\frac{\lambda}{\mathrm{4}\pi\varepsilon_{\mathrm{0}} }\left[\frac{\sqrt{\mathrm{1}+\left(\pi{u}/\mathrm{2}\right)^{\mathrm{2}} }}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }\right]{du} \\ $$

Question Number 163996 Answers: 1 Comments: 0

{ ((9^((a+1)/b) =125)),((5^(b/a) =3)) :} then faind the volve of ((25^b )/(2a^2 ))=?

$$\begin{cases}{\mathrm{9}^{\frac{{a}+\mathrm{1}}{{b}}} =\mathrm{125}}\\{\mathrm{5}^{\frac{{b}}{{a}}} =\mathrm{3}}\end{cases} \\ $$$${then}\:\:{faind}\:{the}\:{volve}\:{of}\:\:\frac{\mathrm{25}^{{b}} }{\mathrm{2}{a}^{\mathrm{2}} }=? \\ $$

Question Number 163993 Answers: 0 Comments: 5

Question Number 163988 Answers: 0 Comments: 1

if here are 20 apple in a box, how many are the significant figures in it?

$${if}\:{here}\:{are}\:\mathrm{20}\:{apple}\:{in}\:{a}\:{box},\:{how}\:{many}\: \\ $$$${are}\:{the}\:{significant}\:{figures}\:{in}\:{it}? \\ $$

Question Number 163985 Answers: 0 Comments: 0

Question Number 163986 Answers: 1 Comments: 0

((1000))^(1/3) ln^(80) (ln(8/5)−ln((8e)/5))^(80) is simplified form equl to=?

$$\sqrt[{\mathrm{3}}]{\mathrm{1000}}{ln}^{\mathrm{80}} \left({ln}\frac{\mathrm{8}}{\mathrm{5}}−{ln}\frac{\mathrm{8}{e}}{\mathrm{5}}\right)^{\mathrm{80}} \\ $$$${is}\:\:\:\:{simplified}\:\:{form}\:\:{equl}\:\:{to}=? \\ $$$$ \\ $$

Question Number 163978 Answers: 0 Comments: 5

Question Number 163976 Answers: 0 Comments: 0

plot the single-side and double-side line spectrum of g(t) g(t)=2sin^2 (10^3 πt)−10sin(10^3 πt−(π/6))

$${plot}\:{the}\:{single}-{side}\:{and}\:{double}-{side} \\ $$$${line}\:{spectrum}\:{of}\:{g}\left({t}\right) \\ $$$${g}\left({t}\right)=\mathrm{2}{sin}^{\mathrm{2}} \left(\mathrm{10}^{\mathrm{3}} \pi{t}\right)−\mathrm{10}{sin}\left(\mathrm{10}^{\mathrm{3}} \pi{t}−\frac{\pi}{\mathrm{6}}\right) \\ $$

Question Number 163974 Answers: 1 Comments: 1

is light a matter?

$${is}\:{light}\:{a}\:{matter}? \\ $$

Question Number 163972 Answers: 0 Comments: 1

Question Number 163968 Answers: 1 Comments: 0

(−2^2 )^3 =?

$$\left(−\mathrm{2}^{\mathrm{2}} \right)^{\mathrm{3}} =? \\ $$

Question Number 163966 Answers: 1 Comments: 0

lim_(x→(π/2)) (((√(2tan^2 x+3))−(√(2tan^2 x+10)))/(cot x)) =?

$$\:\:\:\:\:\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2tan}\:^{\mathrm{2}} \mathrm{x}+\mathrm{3}}−\sqrt{\mathrm{2tan}\:^{\mathrm{2}} \mathrm{x}+\mathrm{10}}}{\mathrm{cot}\:\mathrm{x}}\:=? \\ $$

Question Number 163961 Answers: 1 Comments: 0

lim_(x→1^− ) (e^(1/(x^2 −1)) /(x−1))=?

$$\underset{\mathrm{x}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}\:\frac{\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}} }{\mathrm{x}−\mathrm{1}}=? \\ $$

Question Number 163954 Answers: 4 Comments: 0

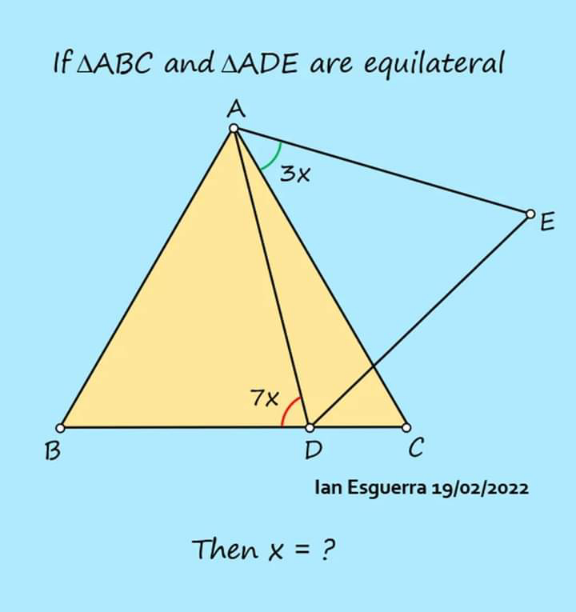
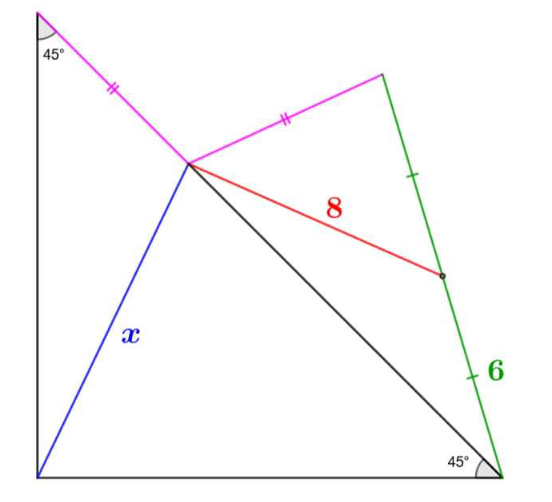
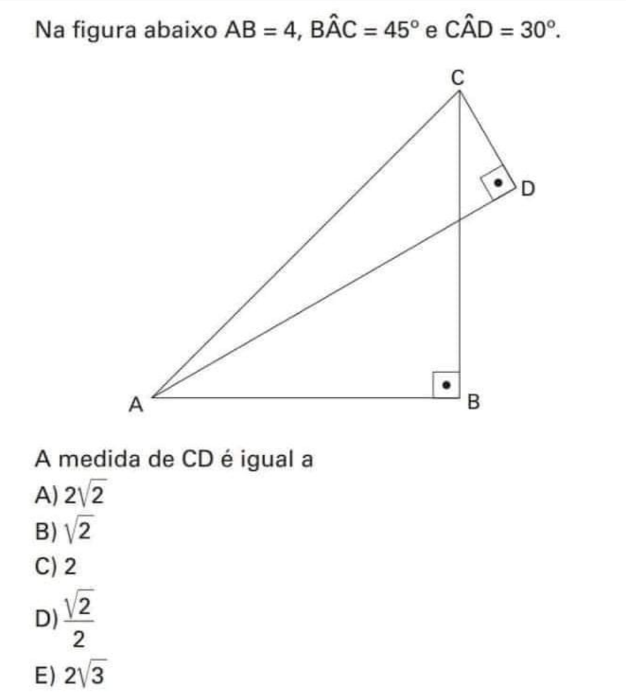
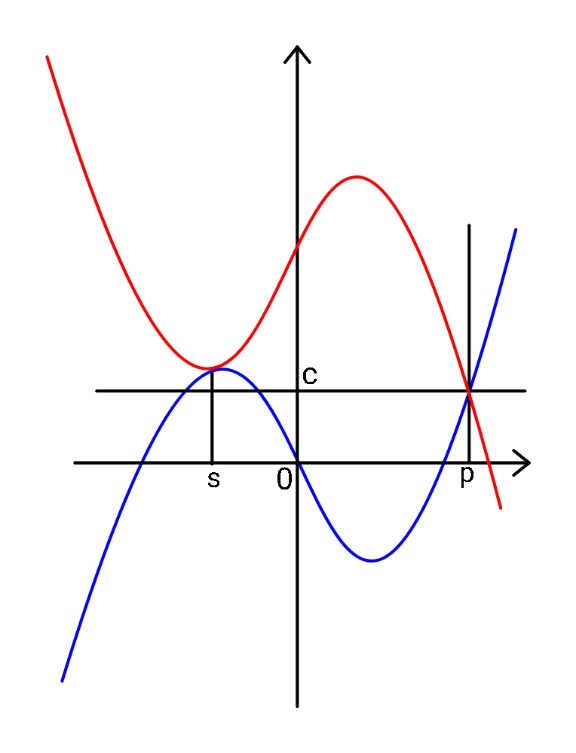
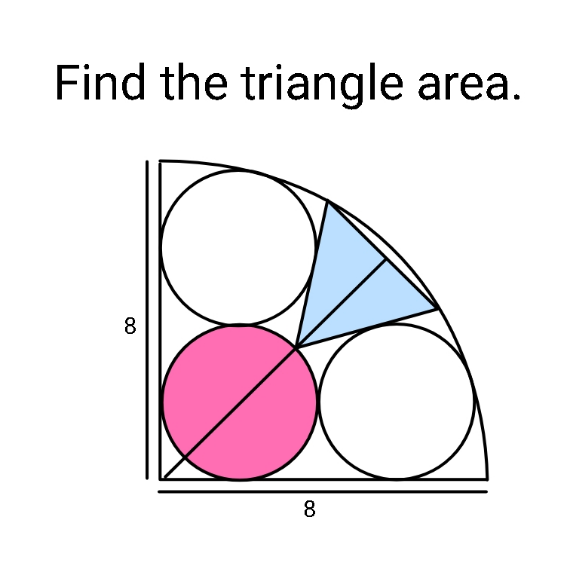
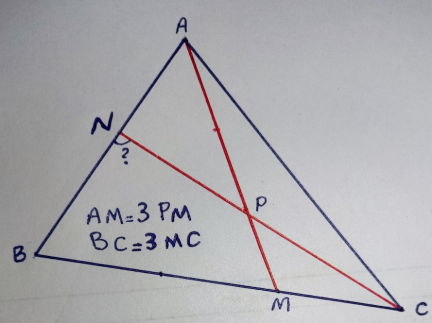
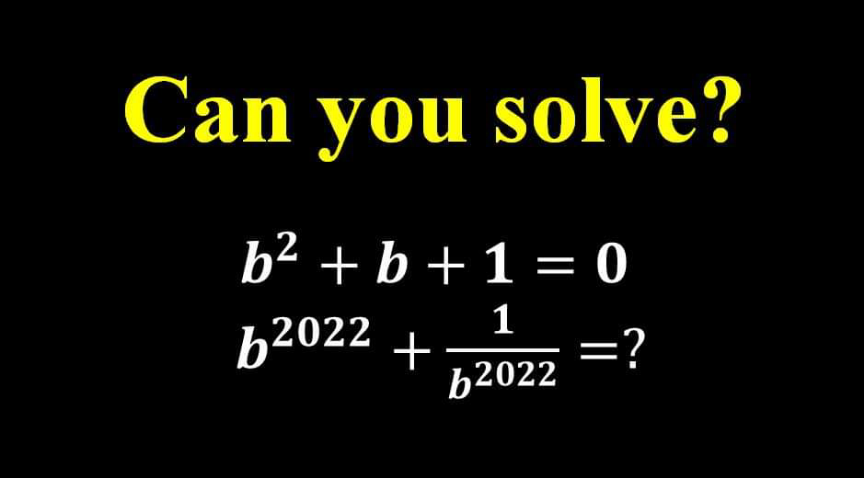
Question Number 163960 Answers: 1 Comments: 0

lim_(x→0) (((√(2+7cot^2 x))−(√(7+7cot^2 x)))/(tan x)) =?

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}+\mathrm{7cot}\:^{\mathrm{2}} \mathrm{x}}−\sqrt{\mathrm{7}+\mathrm{7cot}\:^{\mathrm{2}} \mathrm{x}}}{\mathrm{tan}\:\mathrm{x}}\:=? \\ $$

Question Number 163959 Answers: 0 Comments: 0

Question Number 163958 Answers: 0 Comments: 0

Question Number 163957 Answers: 1 Comments: 0

Question Number 163956 Answers: 0 Comments: 0

Question Number 163955 Answers: 0 Comments: 0

Question Number 163942 Answers: 1 Comments: 0

f(2x)−2[ f(x) ]^2 +1=0 f(x)=?

$${f}\left(\mathrm{2}{x}\right)−\mathrm{2}\left[\:{f}\left({x}\right)\:\right]^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$${f}\left({x}\right)=? \\ $$

Question Number 163939 Answers: 0 Comments: 0

An old unsolved question#1132 let S={1,2,3,4,5}, if A,B,C is such that A∩B∩C=∅ A∩B≠∅ A∩C≠∅ how many ways can be choose A,B and C

$$\mathrm{An}\:\mathrm{old}\:\mathrm{unsolved}\:\mathrm{question}#\mathrm{1132} \\ $$$$\mathrm{let}\:\mathrm{S}=\left\{\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5}\right\},\:\mathrm{if}\:\mathrm{A},\mathrm{B},\mathrm{C}\:\mathrm{is}\:\mathrm{such}\:\mathrm{that} \\ $$$$\mathrm{A}\cap\mathrm{B}\cap\mathrm{C}=\varnothing \\ $$$$\mathrm{A}\cap\mathrm{B}\neq\varnothing \\ $$$$\mathrm{A}\cap\mathrm{C}\neq\varnothing \\ $$$$\mathrm{how}\:\mathrm{many}\:\mathrm{ways}\:\mathrm{can}\:\mathrm{be}\:\mathrm{choose}\:\mathrm{A},\mathrm{B}\:\mathrm{and} \\ $$$$\mathrm{C} \\ $$

Pg 534 Pg 535 Pg 536 Pg 537 Pg 538 Pg 539 Pg 540 Pg 541 Pg 542 Pg 543

Contact: info@tinkutara.com