
AllQuestion and Answers: Page 538
Question Number 166570 Answers: 1 Comments: 0
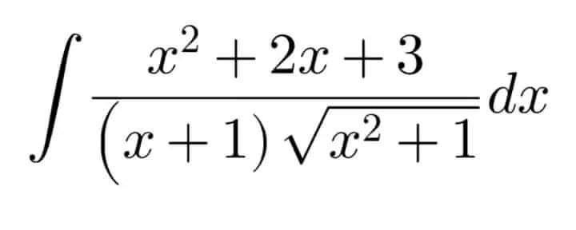
Question Number 166569 Answers: 0 Comments: 0

Question Number 166555 Answers: 0 Comments: 0

Question Number 166554 Answers: 0 Comments: 0
Question Number 166560 Answers: 1 Comments: 0

Question Number 166552 Answers: 0 Comments: 0
Question Number 166542 Answers: 1 Comments: 0

Question Number 166541 Answers: 1 Comments: 0
$${fin}\:\int\:{sec}^{\mathrm{3}} {x}\:{dx}\:{with}\:{out}\:{using}\:{the}\:{bart}\:? \\ $$
Question Number 166539 Answers: 0 Comments: 2
Question Number 166531 Answers: 0 Comments: 2
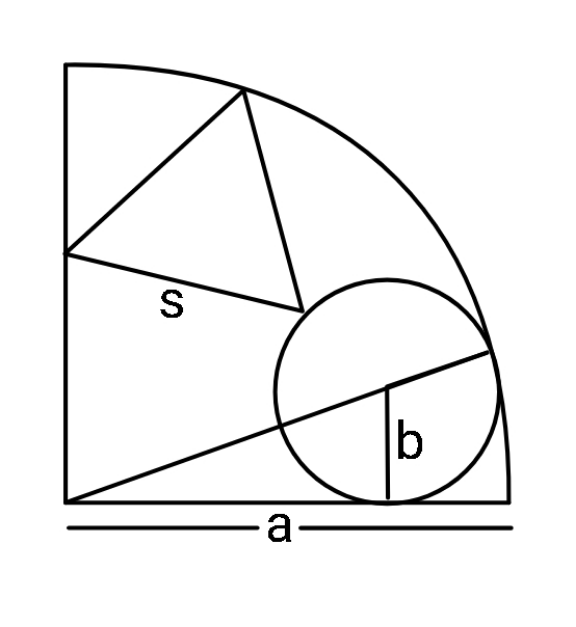
Question Number 166530 Answers: 1 Comments: 0
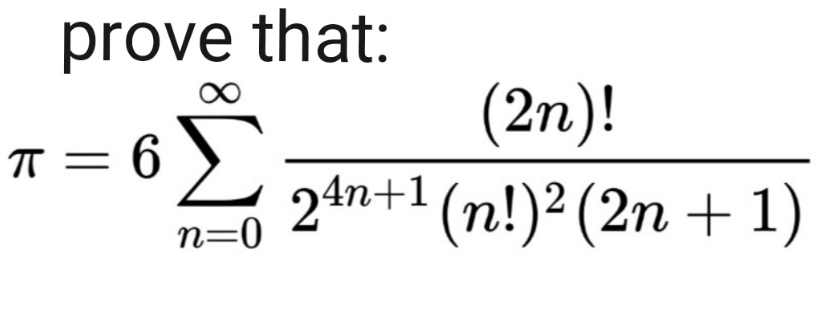
Question Number 166526 Answers: 1 Comments: 0
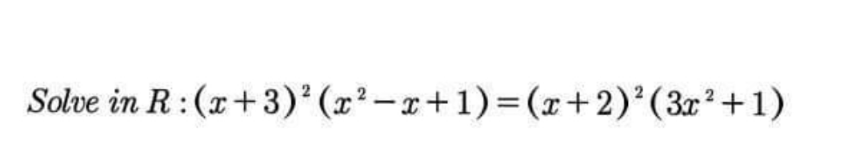
Question Number 166522 Answers: 1 Comments: 1

Question Number 166520 Answers: 2 Comments: 2

Question Number 166516 Answers: 0 Comments: 0
Question Number 166515 Answers: 1 Comments: 0
Question Number 166511 Answers: 1 Comments: 0
Question Number 166496 Answers: 0 Comments: 1
Question Number 166491 Answers: 0 Comments: 4

Question Number 166488 Answers: 1 Comments: 0
Question Number 166481 Answers: 2 Comments: 1

Question Number 166480 Answers: 0 Comments: 0

Question Number 166475 Answers: 2 Comments: 5
Question Number 166468 Answers: 2 Comments: 0
Question Number 166465 Answers: 1 Comments: 1

Question Number 166449 Answers: 1 Comments: 3
Pg 533 Pg 534 Pg 535 Pg 536 Pg 537 Pg 538 Pg 539 Pg 540 Pg 541 Pg 542
