Question and Answers Forum

AllQuestion and Answers: Page 537

Question Number 163008 Answers: 2 Comments: 0

Calculate ∫ (((2−4sin x cos x)(1+sin 2x))/(sin^4 2x+64 cos^4 2x)) dx

$$\:{Calculate}\: \\ $$$$\:\:\:\int\:\frac{\left(\mathrm{2}−\mathrm{4sin}\:{x}\:\mathrm{cos}\:{x}\right)\left(\mathrm{1}+\mathrm{sin}\:\mathrm{2}{x}\right)}{\mathrm{sin}\:^{\mathrm{4}} \mathrm{2}{x}+\mathrm{64}\:\mathrm{cos}\:^{\mathrm{4}} \mathrm{2}{x}}\:{dx}\: \\ $$$$ \\ $$

Question Number 163002 Answers: 0 Comments: 0

prove that i:Σ_(n=0) ^∞ (((−1 )^( n) )/((n +(1/2))cosh(n+(1/2))π)) =(π/4) ii: ∫_0 ^( 1) (( sin( π x ))/(x^( x) ( 1−x )^( 1−x) )) (dx/(1+x)) =(π/4) −−−

$$ \\ $$$$\:\:\:{prove}\:{that} \\ $$$$ \\ $$$$\:{i}:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\left(−\mathrm{1}\:\right)^{\:{n}} }{\left({n}\:+\frac{\mathrm{1}}{\mathrm{2}}\right){cosh}\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\pi}\:=\frac{\pi}{\mathrm{4}} \\ $$$$\:\:{ii}:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:{sin}\left(\:\pi\:{x}\:\right)}{{x}^{\:{x}} \left(\:\mathrm{1}−{x}\:\right)^{\:\mathrm{1}−{x}} }\:\frac{{dx}}{\mathrm{1}+{x}}\:=\frac{\pi}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:−−− \\ $$

Question Number 163000 Answers: 1 Comments: 0

Question Number 162999 Answers: 0 Comments: 0

Question Number 162995 Answers: 1 Comments: 0

if a_k > 0 ; k = 1,5^(−) then prove that exists i,j∈1,5^(−) such that: 0 ≤ ((a_j - a_i )/(1 + a_i a_j )) ≤ (√2) - 1

$$\mathrm{if}\:\:\mathrm{a}_{\boldsymbol{\mathrm{k}}} \:>\:\mathrm{0}\:\:;\:\:\mathrm{k}\:=\:\overline {\mathrm{1},\mathrm{5}} \\ $$$$\mathrm{then}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{exists}\:\:\boldsymbol{\mathrm{i}},\boldsymbol{\mathrm{j}}\in\overline {\mathrm{1},\mathrm{5}}\:\:\mathrm{such}\:\mathrm{that}: \\ $$$$\mathrm{0}\:\leqslant\:\frac{\mathrm{a}_{\boldsymbol{\mathrm{j}}} \:-\:\mathrm{a}_{\boldsymbol{\mathrm{i}}} }{\mathrm{1}\:+\:\mathrm{a}_{\boldsymbol{\mathrm{i}}} \mathrm{a}_{\boldsymbol{\mathrm{j}}} }\:\leqslant\:\sqrt{\mathrm{2}}\:-\:\mathrm{1} \\ $$

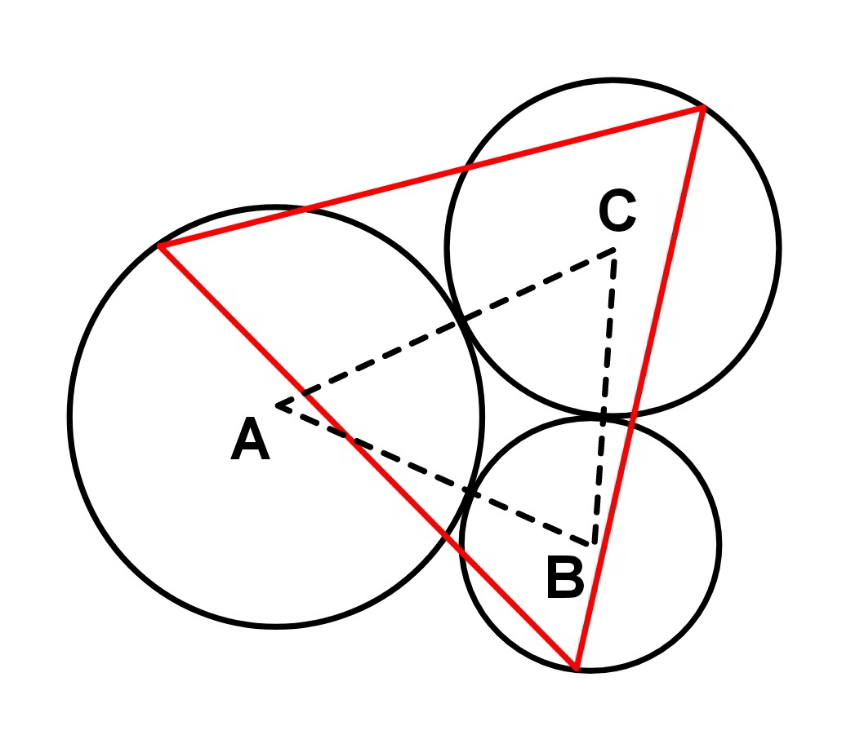
Question Number 162994 Answers: 0 Comments: 0

Question Number 162993 Answers: 0 Comments: 0

Find: 𝛀 =∫_( 0) ^( (𝛑/2)) xcot(x)log(cos(x))dx

$$\mathrm{Find}: \\ $$$$\boldsymbol{\Omega}\:=\underset{\:\mathrm{0}} {\overset{\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} {\int}}\:\mathrm{xcot}\left(\mathrm{x}\right)\mathrm{log}\left(\mathrm{cos}\left(\mathrm{x}\right)\right)\mathrm{dx} \\ $$

Question Number 162974 Answers: 0 Comments: 0

Question Number 162973 Answers: 0 Comments: 0

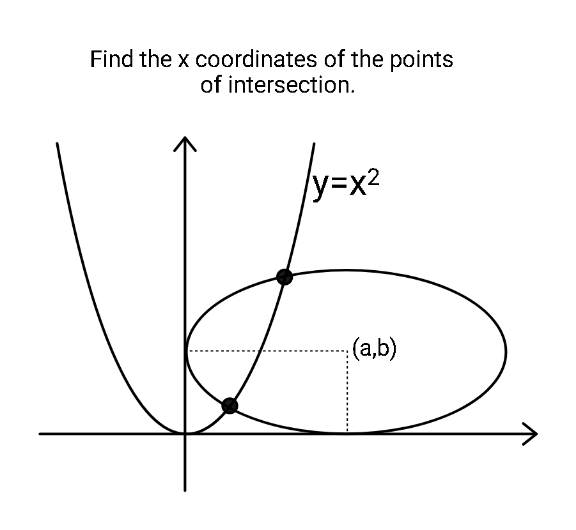
Question Number 162972 Answers: 0 Comments: 0

Question Number 162971 Answers: 0 Comments: 0

Question Number 162960 Answers: 1 Comments: 0

A ∈ M_( n×n) , A^( 3) = O^− Find , ( A−2I )^( −1) =?

$$ \\ $$$$\:\:\:\:\mathrm{A}\:\in\:\mathrm{M}_{\:{n}×{n}} \:\:,\:\:\:\mathrm{A}^{\:\mathrm{3}} =\:\overset{−} {\mathrm{O}}\:\: \\ $$$$\:\:\:\:\:\mathrm{Find}\:,\:\:\:\:\:\:\:\:\left(\:\mathrm{A}−\mathrm{2I}\:\right)^{\:−\mathrm{1}} =? \\ $$$$ \\ $$

Question Number 162959 Answers: 1 Comments: 5

solve the differential equation y = x + p^3

$${solve}\:{the}\:{differential}\:{equation}\:{y}\:=\:{x}\:+\:{p}^{\mathrm{3}} \\ $$

Question Number 162952 Answers: 0 Comments: 0

Question Number 162951 Answers: 1 Comments: 2

4men clear a farm for 8 days and are paid 24$ How long will 6 men take to clear the same farm if they are paid 360$ ?

$$\mathrm{4men}\:\mathrm{clear}\:\mathrm{a}\:\mathrm{farm}\:\mathrm{for}\:\mathrm{8}\:\mathrm{days}\:\mathrm{and}\:\mathrm{are}\:\mathrm{paid}\:\mathrm{24\$} \\ $$$$\mathrm{How}\:\mathrm{long}\:\mathrm{will}\:\mathrm{6}\:\mathrm{men}\:\mathrm{take}\:\mathrm{to}\:\mathrm{clear}\:\mathrm{the}\:\mathrm{same}\:\mathrm{farm} \\ $$$$\mathrm{if}\:\mathrm{they}\:\mathrm{are}\:\mathrm{paid}\:\mathrm{360\$}\:? \\ $$

Question Number 162949 Answers: 3 Comments: 1

Question Number 162947 Answers: 0 Comments: 0

Question Number 162946 Answers: 1 Comments: 0

Question Number 162939 Answers: 0 Comments: 0

lim_( x→ 3) ( a ⌊x ⌋ + ⌊ −x⌋).tan(((πx)/2) )=−∞ a ∈ ?

$$ \\ $$$$\:\:{lim}_{\:{x}\rightarrow\:\mathrm{3}} \:\left(\:{a}\:\lfloor{x}\:\rfloor\:+\:\lfloor\:−{x}\rfloor\right).{tan}\left(\frac{\pi{x}}{\mathrm{2}}\:\right)=−\infty \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{a}\:\in\:? \\ $$$$ \\ $$

Question Number 162942 Answers: 2 Comments: 0

How many positive integers less than 500 can be formed using the numbers 1 , 2 , 3 and 5 for the digits?

$$\mathrm{How}\:\mathrm{many}\:\mathrm{positive}\:\mathrm{integers}\:\mathrm{less}\:\mathrm{than} \\ $$$$\mathrm{500}\:\mathrm{can}\:\mathrm{be}\:\mathrm{formed}\:\mathrm{using}\:\mathrm{the}\:\mathrm{numbers} \\ $$$$\mathrm{1}\:,\:\mathrm{2}\:,\:\mathrm{3}\:\mathrm{and}\:\mathrm{5}\:\mathrm{for}\:\mathrm{the}\:\mathrm{digits}? \\ $$

Question Number 162941 Answers: 0 Comments: 0

Question Number 162926 Answers: 0 Comments: 0

lim_(x→0) (1/x^(n+1) )[(1+x+(x/2)+...+(x^n /n))^(1/(x+(x/2)+...+(x^n /n))) −(1+x+(x/2)+...+(x^(n+1) /(n+1)))^(1/(x+(x/2)+...+(x^(n+1) /(n+1)))) ]=?

$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }\left[\left(\mathrm{1}+\mathrm{x}+\frac{\mathrm{x}}{\mathrm{2}}+...+\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\right)^{\frac{\mathrm{1}}{\mathrm{x}+\frac{\mathrm{x}}{\mathrm{2}}+...+\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}}} −\left(\mathrm{1}+\mathrm{x}+\frac{\mathrm{x}}{\mathrm{2}}+...+\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\right)^{\frac{\mathrm{1}}{\mathrm{x}+\frac{\mathrm{x}}{\mathrm{2}}+...+\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}}} \right]=? \\ $$

Question Number 162925 Answers: 1 Comments: 0

lim_(x→0) (1/x^4 )[(1+x+(x^2 /2)+(x^3 /3))^(1/(x+(x^2 /2)+(x^3 /3))) −(1+x+(x^2 /2)+(x^3 /3)+(x^4 /4))^(1/(x+(x^2 /2)+(x^3 /3)+(x^4 /4))) ]=?

Question Number 162924 Answers: 2 Comments: 0

𝛗 =∫_0 ^( ∞) (( e^( −x^( 2) ) .ln( x ))/( (√x))) dx=λ Γ((1/4)) λ=? ■

$$\: \\ $$$$\:\boldsymbol{\phi}\:=\int_{\mathrm{0}} ^{\:\infty} \frac{\:{e}^{\:−{x}^{\:\mathrm{2}} } .\mathrm{ln}\left(\:{x}\:\right)}{\:\sqrt{{x}}}\:{dx}=\lambda\:\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\lambda=?\:\:\:\:\:\:\:\:\:\:\:\:\:\blacksquare \\ $$$$ \\ $$

Question Number 162894 Answers: 1 Comments: 0

Question Number 162893 Answers: 2 Comments: 0

Ω=∫_0 ^( 1) ((( x^ )/(ln^ ( 1−x ))))^( 2) dx=^? ln ((( 27)/(16)) ) −−−−

$$ \\ $$$$\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{\:{x}^{\:} }{\mathrm{ln}^{\:} \left(\:\mathrm{1}−{x}\:\right)}\right)^{\:\mathrm{2}} {dx}\overset{?} {=}\:\mathrm{ln}\:\left(\frac{\:\mathrm{27}}{\mathrm{16}}\:\right) \\ $$$$\:\:\:\:\:\:\:\:−−−− \\ $$$$ \\ $$

Pg 532 Pg 533 Pg 534 Pg 535 Pg 536 Pg 537 Pg 538 Pg 539 Pg 540 Pg 541

Contact: info@tinkutara.com