Question and Answers Forum

AllQuestion and Answers: Page 536

Question Number 164728 Answers: 3 Comments: 1

Question Number 164705 Answers: 2 Comments: 0

lim_(x→0) (((1^x +2^x +...+n^x )/n))^(1/x)

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}^{{x}} +\mathrm{2}^{{x}} +...+{n}^{{x}} }{{n}}\right)^{\frac{\mathrm{1}}{{x}}} \\ $$

Question Number 164703 Answers: 1 Comments: 0

Question Number 164702 Answers: 1 Comments: 0

lim_(x→0) (((1^x +2^x +∙∙∙+n^x )/n))^(1/x) =?

$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\left(\frac{\mathrm{1}^{{x}} +\mathrm{2}^{{x}} +\centerdot\centerdot\centerdot+{n}^{{x}} }{{n}}\right)^{\frac{\mathrm{1}}{{x}}} =? \\ $$

Question Number 164699 Answers: 0 Comments: 0

Question Number 164686 Answers: 1 Comments: 0

∫36x^2 (2x+3)^(−7) dx

$$\int\mathrm{36}\boldsymbol{{x}}^{\mathrm{2}} \:\left(\mathrm{2}\boldsymbol{{x}}+\mathrm{3}\right)^{−\mathrm{7}} \:\boldsymbol{{dx}} \\ $$$$\: \\ $$

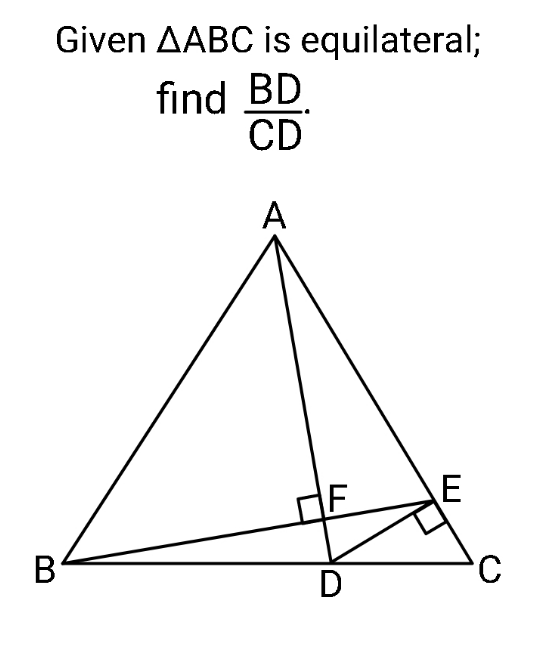
Question Number 164685 Answers: 1 Comments: 0

∫4x^2 (1−x)^3 dx

$$\int\mathrm{4}\boldsymbol{{x}}^{\mathrm{2}} \:\left(\mathrm{1}−\boldsymbol{{x}}\right)^{\mathrm{3}} \:\boldsymbol{{dx}} \\ $$

Question Number 164684 Answers: 1 Comments: 0

∫24(2x−1)^(−3) dx

$$\int\mathrm{24}\left(\mathrm{2}\boldsymbol{{x}}−\mathrm{1}\right)^{−\mathrm{3}} \:\boldsymbol{{dx}} \\ $$

Question Number 164683 Answers: 1 Comments: 0

∫(x^2 /((x+7)^4 ))dx

$$\int\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\left(\boldsymbol{{x}}+\mathrm{7}\right)^{\mathrm{4}} }\boldsymbol{{dx}} \\ $$

Question Number 164682 Answers: 1 Comments: 0

∫27x^2 (√(3x−2)) dx

$$\int\mathrm{27}\boldsymbol{{x}}^{\mathrm{2}} \:\sqrt{\mathrm{3}\boldsymbol{{x}}−\mathrm{2}}\:\boldsymbol{{dx}} \\ $$

Question Number 164681 Answers: 1 Comments: 0

∫ (−8x(√(3−2x)) )dx

$$\int\:\left(−\mathrm{8}\boldsymbol{{x}}\sqrt{\mathrm{3}−\mathrm{2}\boldsymbol{{x}}}\:\right)\boldsymbol{{dx}} \\ $$

Question Number 164680 Answers: 0 Comments: 0

what is the proof of stirling′s formula without gamma function?

$${what}\:{is}\:{the}\:{proof}\:{of}\:{stirling}'{s}\:{formula} \\ $$$${without}\:{gamma}\:{function}? \\ $$

Question Number 164675 Answers: 0 Comments: 5

Question Number 164674 Answers: 0 Comments: 0

Question Number 164672 Answers: 1 Comments: 0

Question Number 164671 Answers: 1 Comments: 1

solve cos^( 3) (x) + sin^( 2) (x) = (7/8) adopted from youtube ...

$$ \\ $$$$\:\:\:\:\:\:\:\:{solve}\: \\ $$$$\:\:\:\:\:\:{cos}^{\:\mathrm{3}} \left({x}\right)\:+\:{sin}^{\:\mathrm{2}} \left({x}\right)\:=\:\frac{\mathrm{7}}{\mathrm{8}}\: \\ $$$$\:\:\:\:\:\:\:\:\:{adopted}\:{from}\:{youtube}\:... \\ $$$$ \\ $$

Question Number 164669 Answers: 0 Comments: 0

Question Number 164650 Answers: 1 Comments: 0

((x+9))^(1/3) −((x−9))^(1/3) = 3 x=?

$$\:\:\sqrt[{\mathrm{3}}]{{x}+\mathrm{9}}\:−\sqrt[{\mathrm{3}}]{{x}−\mathrm{9}}\:=\:\mathrm{3}\: \\ $$$$\:{x}=? \\ $$

Question Number 164653 Answers: 2 Comments: 0

solve 𝛗 = ∫_0 ^( 1) ((ln^( 2) ( x ). tanh^( −1) ( x ))/x)dx =? Ω= ∫_0 ^( 1) (( (tanh^(−1) (x))^( 2) )/(1+x)) = ? −−−−

$$ \\ $$$$\:\:\:\:\:\:\:\:{solve} \\ $$$$\:\:\boldsymbol{\phi}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{ln}^{\:\mathrm{2}} \left(\:{x}\:\right).\:{tanh}^{\:−\mathrm{1}} \left(\:{x}\:\:\right)}{{x}}{dx}\:=? \\ $$$$\:\:\:\Omega=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:\left({tanh}^{−\mathrm{1}} \left({x}\right)\right)^{\:\mathrm{2}} }{\mathrm{1}+{x}}\:=\:? \\ $$$$\:\:\:\:\:\:−−−− \\ $$

Question Number 164639 Answers: 1 Comments: 0

Question Number 164628 Answers: 1 Comments: 1

60!=abc…nm000…0 m=? n=?

$$\mathrm{60}!=\underline{\boldsymbol{\mathrm{abc}}\ldots\boldsymbol{\mathrm{nm}}\mathrm{000}\ldots\mathrm{0}} \\ $$$$\boldsymbol{\mathrm{m}}=?\:\:\boldsymbol{\mathrm{n}}=? \\ $$

Question Number 164627 Answers: 1 Comments: 0

Question Number 164626 Answers: 1 Comments: 1

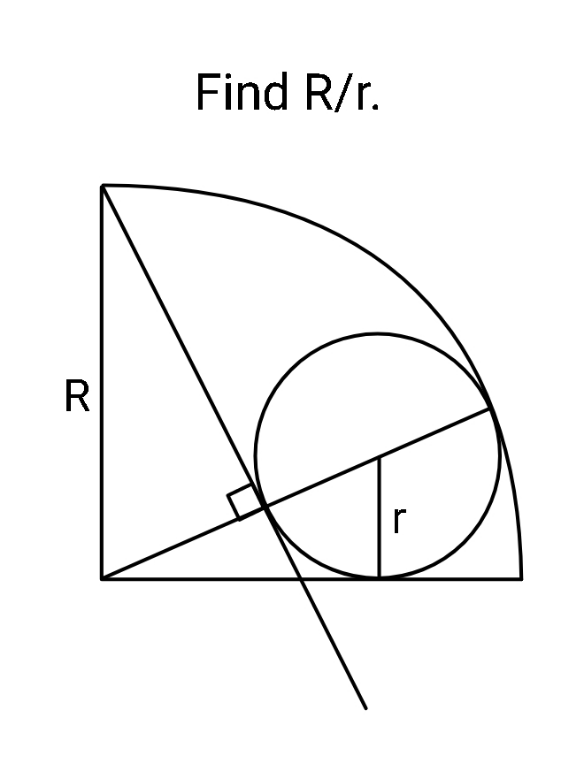
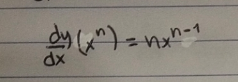
Question Number 164623 Answers: 1 Comments: 0

Given a, b ∈ R. Show that : [a]+[b]≤[a+b]≤[a]+[b]+1

$${Given}\:{a},\:{b}\:\in\:\mathbb{R}. \\ $$$${Show}\:{that}\:: \\ $$$$\left[{a}\right]+\left[{b}\right]\leqslant\left[{a}+{b}\right]\leqslant\left[{a}\right]+\left[{b}\right]+\mathrm{1} \\ $$

Question Number 164622 Answers: 2 Comments: 0

Show that ∀ a, b ∈ R, 1. ∣∣x∣−∣y∣∣≤∣x−y∣ 2. 1+∣xy−1∣≤(1+∣x−1∣)(1+∣y−1∣).

$${Show}\:{that}\:\forall\:{a},\:{b}\:\in\:\mathbb{R}, \\ $$$$\mathrm{1}.\:\mid\mid{x}\mid−\mid{y}\mid\mid\leqslant\mid{x}−{y}\mid \\ $$$$\mathrm{2}.\:\mathrm{1}+\mid{xy}−\mathrm{1}\mid\leqslant\left(\mathrm{1}+\mid{x}−\mathrm{1}\mid\right)\left(\mathrm{1}+\mid{y}−\mathrm{1}\mid\right). \\ $$

Question Number 164615 Answers: 0 Comments: 0

Pg 531 Pg 532 Pg 533 Pg 534 Pg 535 Pg 536 Pg 537 Pg 538 Pg 539 Pg 540

Contact: info@tinkutara.com