Question and Answers Forum

AllQuestion and Answers: Page 535

Question Number 160384 Answers: 2 Comments: 0

lim_(n→∞) n∫_1 ^(1+(1/n)) (√(1+x^n ))dx=?

$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}n}\int_{\mathrm{1}} ^{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}} \sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{n}} }\mathrm{dx}=? \\ $$

Question Number 160375 Answers: 1 Comments: 2

Question Number 160373 Answers: 2 Comments: 0

Compare it: ((1 - sin (10°))/(cos (10°))) and 1

$$\mathrm{Compare}\:\mathrm{it}: \\ $$$$\frac{\mathrm{1}\:-\:\mathrm{sin}\:\left(\mathrm{10}°\right)}{\mathrm{cos}\:\left(\mathrm{10}°\right)}\:\:\:\:\:\mathrm{and}\:\:\:\:\:\mathrm{1} \\ $$

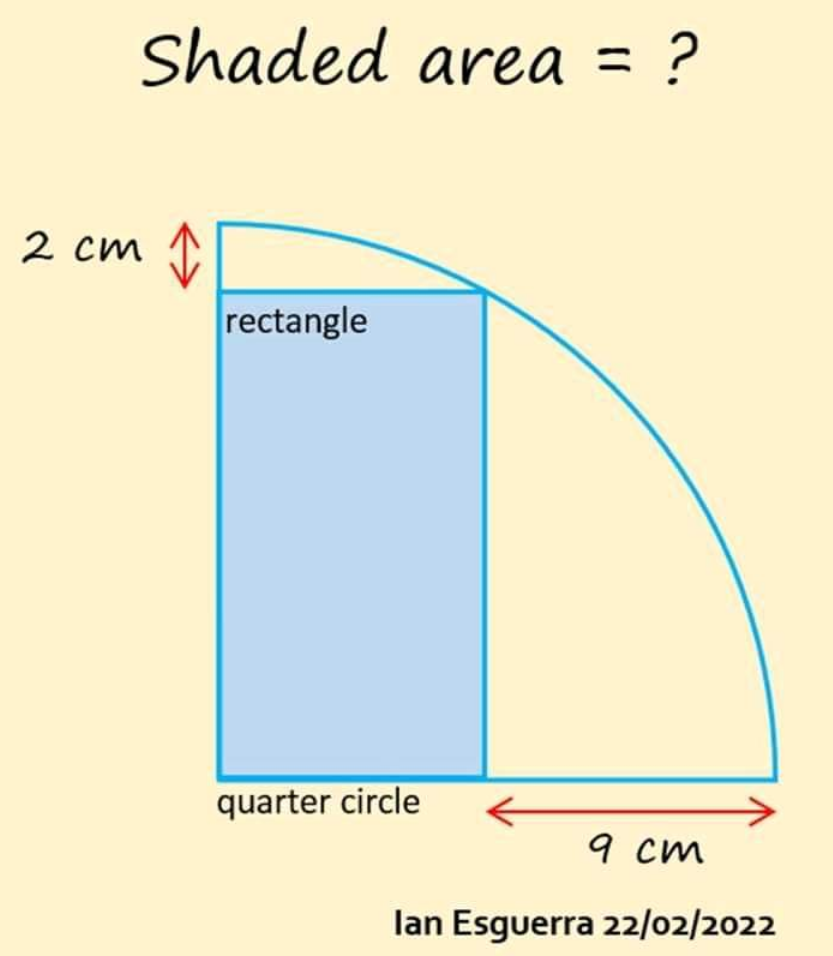
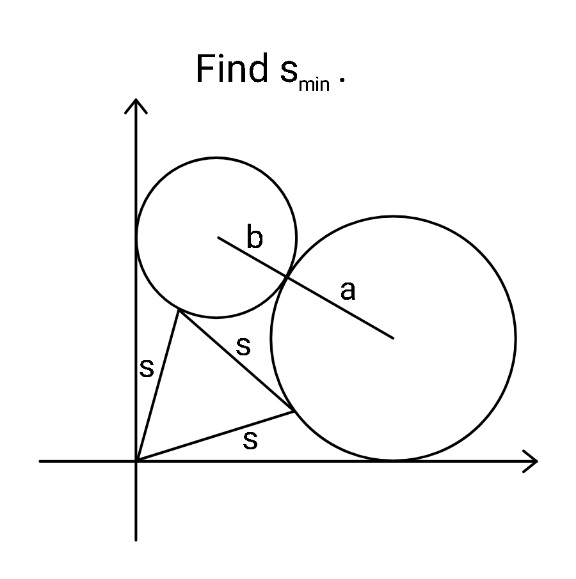
Question Number 160372 Answers: 1 Comments: 0

Calculate Σ_(k=0) ^(2000) i^k , Σ_(k=0) ^(2002) (−1)^k

$${Calculate} \\ $$$$\sum_{{k}=\mathrm{0}} ^{\mathrm{2000}} {i}^{{k}} ,\:\:\sum_{{k}=\mathrm{0}} ^{\mathrm{2002}} \left(−\mathrm{1}\right)^{{k}} \\ $$

Question Number 160371 Answers: 2 Comments: 0

lim_(t→a) (((alnt−tlna)^2 (tlnt−alna))/(2(t−a)(t−a−aln(t/a)))) please help me.

$${li}\underset{{t}\rightarrow{a}} {{m}}\frac{\left({alnt}−{tlna}\right)^{\mathrm{2}} \left({tlnt}−{alna}\right)}{\mathrm{2}\left({t}−{a}\right)\left({t}−{a}−{aln}\frac{{t}}{{a}}\right)} \\ $$$${please}\:{help}\:{me}. \\ $$

Question Number 160363 Answers: 0 Comments: 0

s>0 limΣ_(k=1) ^(2n) ( −1)^( k) .((( k)/(2n)) )^( s) = ?

$$ \\ $$$$\:\:\:\:\:{s}>\mathrm{0} \\ $$$$\:\:\:\:{lim}\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{n}} {\sum}}\left(\:−\mathrm{1}\right)^{\:{k}} .\left(\frac{\:{k}}{\mathrm{2}{n}}\:\right)^{\:{s}} =\:\:? \\ $$

Question Number 160362 Answers: 0 Comments: 0

∫(x^n /( (√(x−x^2 ))))dx=?

$$\int\frac{\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{n}}} }{\:\sqrt{\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} }}\boldsymbol{\mathrm{dx}}=? \\ $$

Question Number 160361 Answers: 0 Comments: 0

1^o Prove by recrrence that , for n≥28 , n!≥11^n . 2^o Deduce the limite of the suite (((n!)/(10^n ))) when n tend verse +∞.

$$\mathrm{1}^{{o}} \:{Prove}\:{by}\:{recrrence}\:{that}\:,\:{for} \\ $$$${n}\geqslant\mathrm{28}\:,\:\:{n}!\geqslant\mathrm{11}^{{n}} . \\ $$$$\mathrm{2}^{{o}} \:{Deduce}\:{the}\:{limite}\:{of}\:{the}\:{suite} \\ $$$$\left(\frac{{n}!}{\mathrm{10}^{{n}} }\right)\:{when}\:{n}\:{tend}\:{verse}\:+\infty. \\ $$

Question Number 160358 Answers: 1 Comments: 0

∫_0 ^(π/2) ln(sinx)ln(cosx)dx

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}{x}\right)\mathrm{ln}\left(\mathrm{cos}{x}\right){dx} \\ $$

Question Number 160353 Answers: 1 Comments: 0

Question Number 160350 Answers: 1 Comments: 0

Question Number 160349 Answers: 1 Comments: 0

find ∫(dx/(x+e^x ))=?

$${find}\:\int\frac{{dx}}{{x}+{e}^{{x}} }=? \\ $$

Question Number 160344 Answers: 3 Comments: 0

compare the following numbers ((12)/(15)) ,(3/5)

$${compare}\:{the}\:{following}\:{numbers}\:\frac{\mathrm{12}}{\mathrm{15}}\:,\frac{\mathrm{3}}{\mathrm{5}} \\ $$

Question Number 160342 Answers: 1 Comments: 0

Question Number 160333 Answers: 0 Comments: 1

Question Number 160325 Answers: 1 Comments: 3

Question Number 160327 Answers: 0 Comments: 0

y = kx ; y = (k/x) ; x = k + 1 find the area of the surrounded figure

$$\mathrm{y}\:=\:\mathrm{kx}\:\:;\:\:\mathrm{y}\:=\:\frac{\mathrm{k}}{\mathrm{x}}\:\:;\:\:\mathrm{x}\:=\:\mathrm{k}\:+\:\mathrm{1} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{surrounded}\:\mathrm{figure} \\ $$$$ \\ $$

Question Number 160879 Answers: 1 Comments: 1

Question Number 160317 Answers: 1 Comments: 1

Question Number 160341 Answers: 0 Comments: 3

f(f(x))=10x^2 −f(x) faind f(x)

$${f}\left({f}\left({x}\right)\right)=\mathrm{10}{x}^{\mathrm{2}} −{f}\left({x}\right)\:\:\:\:\:\:{faind}\:\:\:{f}\left({x}\right) \\ $$

Question Number 160314 Answers: 0 Comments: 2

suppose the probability of a child being a boy is 0.5. Find the probability that a family of 3 children will have (i) at least two boys (ii) exactly two boys (iii) all girls

$${suppose}\:{the}\:{probability}\:{of}\:{a}\:{child} \\ $$$${being}\:{a}\:{boy}\:{is}\:\mathrm{0}.\mathrm{5}.\:{Find}\:{the}\: \\ $$$${probability}\:{that}\:{a}\:{family}\:{of}\: \\ $$$$\:\mathrm{3}\:{children}\:{will}\:{have}\: \\ $$$$\left({i}\right)\:{at}\:{least}\:{two}\:{boys} \\ $$$$\left({ii}\right)\:{exactly}\:{two}\:{boys} \\ $$$$\left({iii}\right)\:{all}\:{girls} \\ $$

Question Number 160310 Answers: 0 Comments: 1

find the period of the function: y = tan ((πx)/k) + cos ((2πx)/(k + 5))

$$\mathrm{find}\:\mathrm{the}\:\mathrm{period}\:\mathrm{of}\:\mathrm{the}\:\mathrm{function}: \\ $$$$\mathrm{y}\:=\:\mathrm{tan}\:\frac{\pi\mathrm{x}}{\mathrm{k}}\:+\:\mathrm{cos}\:\frac{\mathrm{2}\pi\mathrm{x}}{\mathrm{k}\:+\:\mathrm{5}} \\ $$

Question Number 160330 Answers: 0 Comments: 0

(du/dx) = e^(((x/u))) find u

$$\frac{{du}}{{dx}}\:=\:{e}^{\left(\frac{{x}}{{u}}\right)} \\ $$$${find}\:{u} \\ $$

Question Number 160328 Answers: 0 Comments: 0

∫_1 ^( 2e) (√(((x^2 +1)/(ln x)) (√(ln x^2 )))) dx =?

$$\:\int_{\mathrm{1}} ^{\:\mathrm{2e}} \:\sqrt{\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{ln}\:\mathrm{x}}\:\sqrt{\mathrm{ln}\:\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx}\:=? \\ $$

Question Number 160305 Answers: 0 Comments: 0

Question Number 160304 Answers: 0 Comments: 0

Pg 530 Pg 531 Pg 532 Pg 533 Pg 534 Pg 535 Pg 536 Pg 537 Pg 538 Pg 539

Contact: info@tinkutara.com