
AllQuestion and Answers: Page 534
Question Number 166982 Answers: 1 Comments: 3
Question Number 167098 Answers: 3 Comments: 0
Question Number 166975 Answers: 3 Comments: 3
Question Number 166959 Answers: 1 Comments: 0
Question Number 166958 Answers: 3 Comments: 1
Question Number 166956 Answers: 1 Comments: 0
Question Number 166954 Answers: 1 Comments: 0
Question Number 166950 Answers: 0 Comments: 3

Question Number 166943 Answers: 1 Comments: 2

Question Number 166940 Answers: 1 Comments: 0

Question Number 166939 Answers: 1 Comments: 0
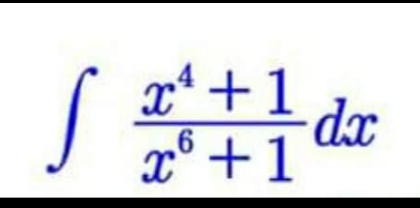
Question Number 166929 Answers: 1 Comments: 0
Question Number 166928 Answers: 1 Comments: 0
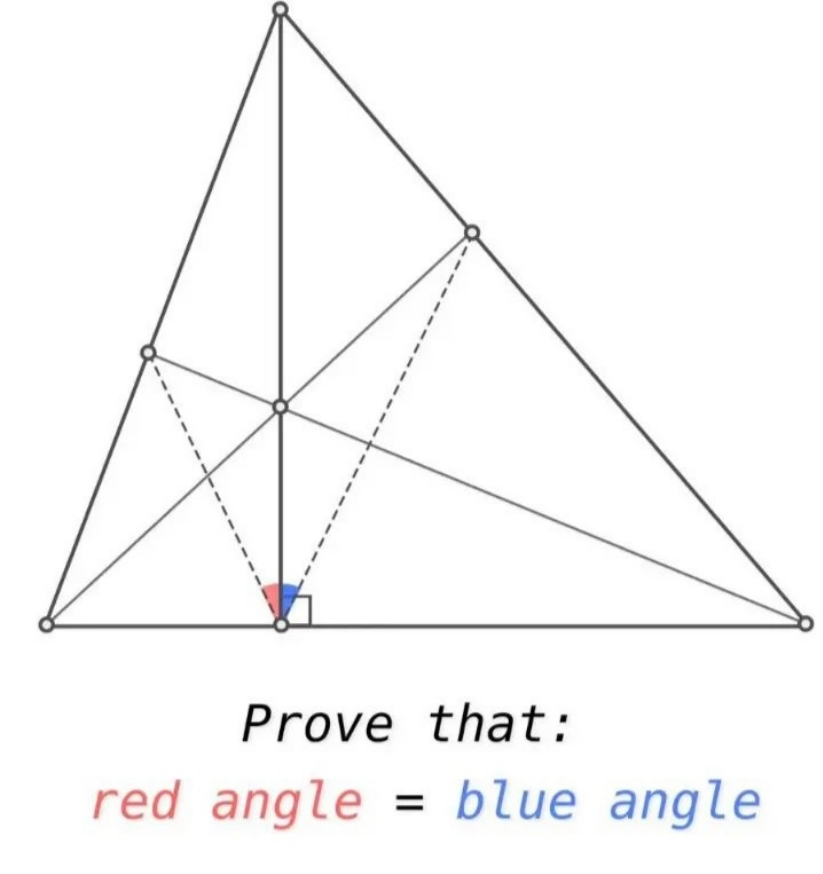
Question Number 166926 Answers: 3 Comments: 0
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{5}^{{n}} }{{n}!}=? \\ $$
Question Number 166917 Answers: 2 Comments: 4
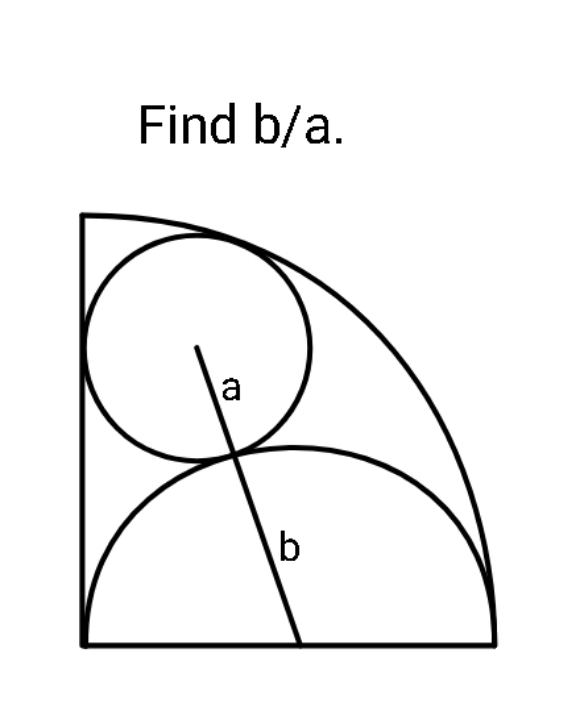
Question Number 166916 Answers: 0 Comments: 0
Question Number 166911 Answers: 1 Comments: 0
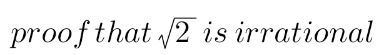
Question Number 166910 Answers: 1 Comments: 1
$${given}\:{that}\:{is}\:{prime},{proof}\:{that}\:\sqrt{{p}}\:{is}\: \\ $$$${irrational} \\ $$
Question Number 166904 Answers: 1 Comments: 0
Question Number 166881 Answers: 0 Comments: 0
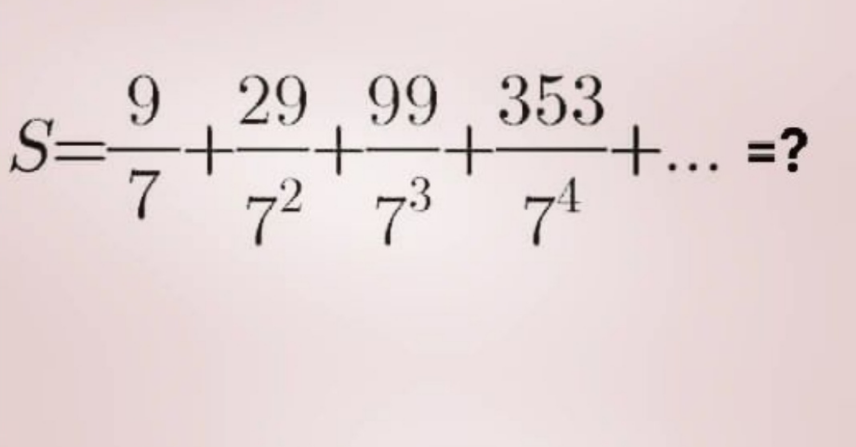
Question Number 166922 Answers: 0 Comments: 0
Question Number 166921 Answers: 0 Comments: 1
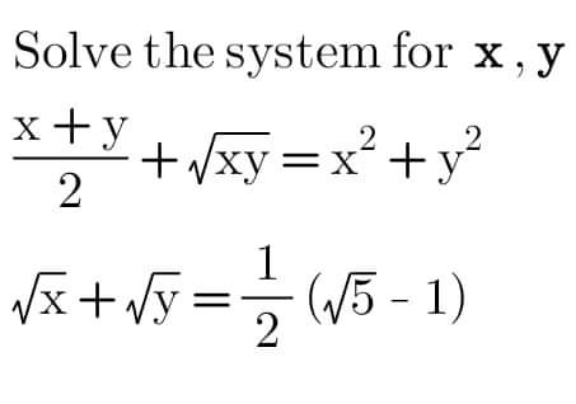
Question Number 166875 Answers: 2 Comments: 1

Question Number 166872 Answers: 2 Comments: 0
Question Number 166861 Answers: 3 Comments: 7
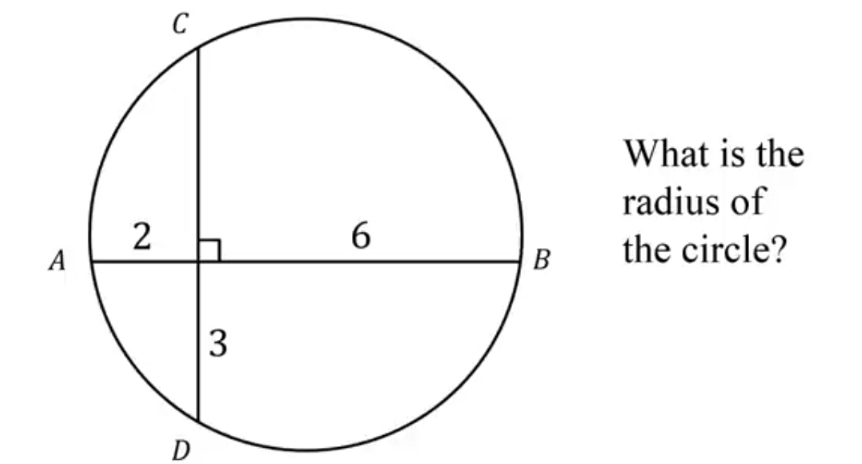
Question Number 166839 Answers: 1 Comments: 0
Pg 529 Pg 530 Pg 531 Pg 532 Pg 533 Pg 534 Pg 535 Pg 536 Pg 537 Pg 538
